cho (p) y=2x2 tìm giá trị của a,b sao cho đường thẳng y=ax+b tiếp xúc với (p) vad đi qua A(0;-2)

Những câu hỏi liên quan
Bài 1: Cho parabol (P): y = 2x2.
1. Tìm giá trị của a,b sao cho đường thẳng y = ax+b tiếp xúc với (P) và đi qua A(0;-2).
2. Tìm phương trình đường thẳng tiếp xúc với (P) tại B(1;2).
3. Tìm giao điểm của (P) với đường thẳng y = 2m +1.
1, - Xét phương trình hoành độ giao điểm :\(2x^2=ax+b\)
\(\Rightarrow2x^2-ax-b=0\left(I\right)\)
Mà (P) tiếp xúc với d .
Nên PT ( I ) có duy nhất một nghiệm .
\(\Leftrightarrow\Delta=\left(-a\right)^2-4.2.\left(-b\right)=a^2+8b=0\)
Lại có : d đi qua A .
\(\Rightarrow b+0a=-2=b\)
\(\Rightarrow a=4\)
2. Tương tự a
3. - Xét phương trình hoành độ giao điểm :\(2x^2=2m+1\)
\(\Rightarrow2x^2-2m-1=0\)
Có : \(\Delta^,=\left(-m\right)^2-\left(-1\right).2=m^2+3\)
=> Giao điểm của P và d là : \(\left\{{}\begin{matrix}x_1=\dfrac{m+\sqrt{m^2+3}}{2}\\x_2=\dfrac{m-\sqrt{m^2+3}}{2}\end{matrix}\right.\)
Đúng 2
Bình luận (0)
Bài 1. Cho parabol (P): y = 2x2.
1. Tìm giá trị của a,b sao cho đường thẳng y = ax+b tiếp xúc với (P) và đi qua A(0;-2).
2. Tìm phương trình đường thẳng tiếp xúc với (P) tại B(1;2).
3. Tìm giao điểm của (P) với đường thẳng y = 2m +1.
Do đường thẳng đã cho đi qua A(−1,0)A(−1,0) nên
0=−a+b0=−a+b
<−>a=b<−>a=b
Xét ptrinh hoành độ giao điểm
12x2=ax+a12x2=ax+a
<−>x2−2ax−2a=0<−>x2−2ax−2a=0
Do hai đồ thị tiếp xúc nên ptrinh trên có 1 nghiệm duy nhất, tức là Δ′=0Δ′=0 hay
a2+2a=0a2+2a=0
<−>a(a+2)=0<−>a(a+2)=0
Vậy a=0a=0 hoặc a=−2a=−2
Do a≠0a≠0 nên a=−2a=−2.
Vậy y=−2x−2y=−2x−2
Trong hệ trục tọa độ Oxy, cho đường thẳng (d): y=6x+b và parabol (P): y=a\(x^2\) (a≠0)
a) Tìm giá trị của b để đường thẳng (d) đi qua điểm M(0;9).
b) Với b tìm được, tìm giá trị câu a để (d) tiếp xúc với (P).
a: Thay x=0 và y=9 vào (d), ta được:
\(b+6\cdot0=9\)
hay b=9
Vậy: (d): y=6x+9
b: Phương trình hoành độ giao điểm là:
\(ax^2-6x-9=0\)
\(\text{Δ}=\left(-6\right)^2-4\cdot a\cdot\left(-9\right)=36a+36\)
Để (d) tiếp xúc với (P) thì 36a+36=0
hay a=-1
Đúng 5
Bình luận (0)
`a)` Vì `(d)` đi qua `M(0;9)` nên thay `x=0` và `y=9` vào `(d)` có: `b=9`
`b)` Với `b=9=>(d):y=6x+9`
Xét ptr hoành độ của `(d)` và `(P)` có:
`ax^2=6x+9`
`<=>ax^2-6x-9=0` `(1)`
Để `(d)` tiếp xúc với `(P)` thì ptr `(1)` có nghiệm kép
`<=>\Delta' =0`
`<=>(-3)^2-a.(-9)=0`
`<=>a=-1` (t/m)
Đúng 4
Bình luận (0)
\(M\left(0;9\right)\in\left(d\right):y=6x+b\Rightarrow9=6\cdot0+b\Rightarrow b=3\)
Ptr hoành độ giao điểm của (P) và (d):
\(ax^2=6x+3\Leftrightarrow ax^2-6x-3=0\)
Để (d) tiếp xúc với (P) thì ptr có nghiệm kép:
\(\left\{{}\begin{matrix}a\ne0\\\Delta=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a\ne0\\\left(-6\right)^2-4\cdot a\cdot\left(-3\right)=0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}a\ne0\\12a=36\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a\ne0\\a=3\end{matrix}\right.\Rightarrow}a=3}\)
Đúng 2
Bình luận (0)
Xem thêm câu trả lời
a. Không sử dụng máy tính cầm tay, giải hệ phương trình $\left\{ \begin{aligned} & 4x - y = 7\\ & x + 3y = 5\\ \end{aligned}\right.$.
b. Cho đường thẳng $d:$ $y = ax + b$. Tìm giá trị của $a$ và $b$ sao cho đường thẳng $d$ đi qua điểm $A ( 0; -1)$ và song song với đường thẳng $\Delta :$ $y = x + 2019$.
a, \(\hept{\begin{cases}4x-y=7\\x+3y=5\end{cases}}\Leftrightarrow\hept{\begin{cases}y=4x-7\left(1\right)\\x+3y=5\left(2\right)\end{cases}}\)
Thế (1) vào (2) ta được : \(x+3\left(4x-7\right)=5\Leftrightarrow x+12x-21=5\)
\(\Leftrightarrow13x=26\Leftrightarrow x=2\)
Theo (1) ta có : \(y=8-7=1\)
Vậy \(\left(x;y\right)=\left(2;1\right)\)
a, x = 2 , y = 1
b, a = 1 , b = -1
Xem thêm câu trả lời
Tìm các giá trị của a để luôn tìm được b sao cho
∆
:
y
a
x
+
b
tiếp xúc với (C): y
3
x
-
x
3
Đọc tiếp
Tìm các giá trị của a để luôn tìm được b sao cho ∆ : y = a x + b tiếp xúc với (C): y= 3 x - x 3
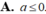
![]()
![]()
![]()
cho P :\(y=-\dfrac{1}{4}x^2\) xác định hệ số a, b của đường thẳng y=ax+b biết đồ thị của nó đi qua A(-1;3) và tiếp xúc với P
Thay x=-1 và y=3 vào (d), ta được:
b-a=3
=>b=a+3
PTHĐGĐ là:
-1/4x^2-ax-b=0
=>x^2+4ax+4b=0
Δ=(4a)^2-4*4b=16a^2-16b
Để (P) tiếp xúc (d) thì 16a^2-16b=0
=>a^2=b
=>a^2=a+3
=>a=(1+căn 13)/2 hoặc a=(1-căn 13)/2
=>b=(7+căn 13)/2 hoặc b=(7-căn 13)/2
Đúng 0
Bình luận (0)
Cho (P) : y = 1/2x2 và (d) : y = ax + b
a. Xác định a và b để đường thẳng (d) đi qua điểm A(-1;0) và tiếp xúc với (P)
b. Tìm tọa độ tiếp điểm
Bài 1 :Giả sử đường thẳng (d) có phương trình y=ax+b . Xác định a,b để (d) đi qua hai điểm A(1;3) và B(-3;-1)
Bài 2 Cho hàm số y=x+m (d). Tìm các giá trị của m để đường thẳng (d)
1, Đi qua điểm A(1;2003)
2, Song song với đường thẳng x-y+3=0
Cho hàm sô y= kx2 có đồ thị (P) và đường thẳng d đi qua hai điểm A(1;3) và B (-1;-5)
A. Viết phương trình của đường thẳng d
B. Tìm giá trị của k để đường thẳng d tiếp xúc với đồ thị (P) . Xác định toạ độ tiếp điểm

























