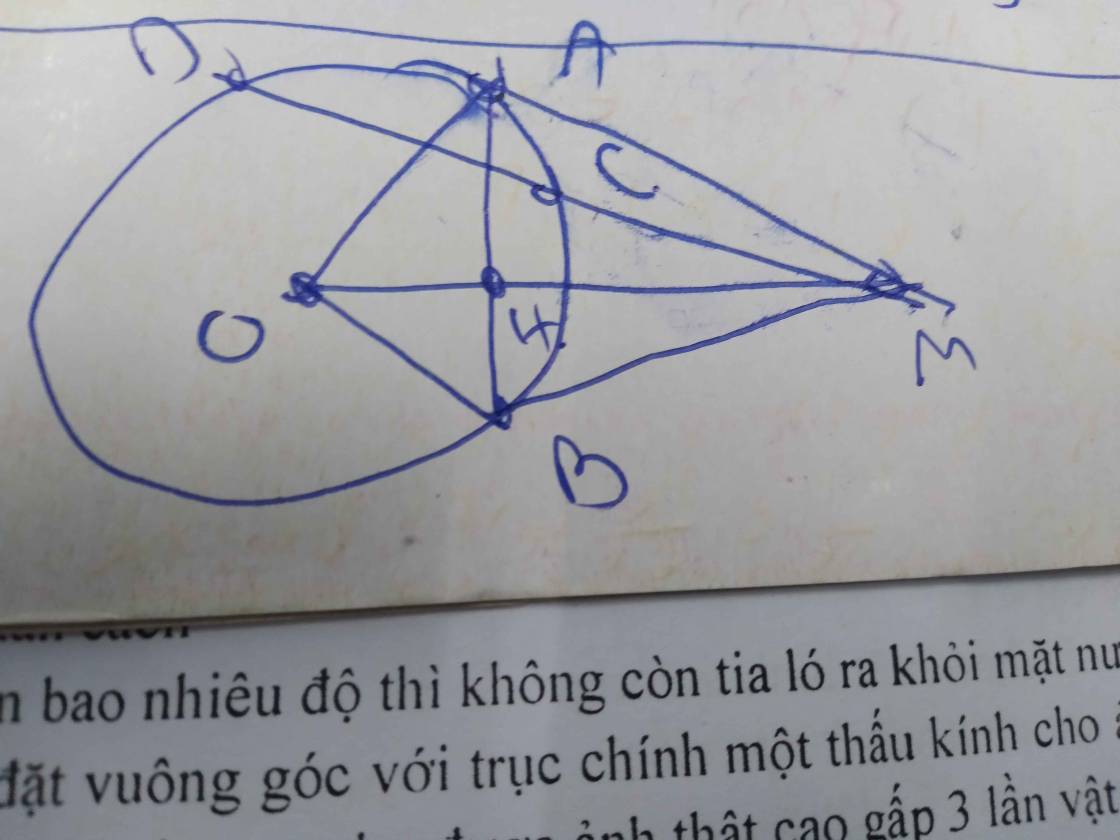
Cho M là một điểm nằm ngoài (O). Kẻ các tiếp tuyến MA; MB với đường tròn; AB là tiếp điểm. Từ A kẻ đưởng thẳng song song với MB cắt (O) tại C. MC cắt (O) tại E, các tia AE; MB cắt nhau tại K. Chứng minh:
a) Tứ giác MAOB nội tiếp
b) MK2=AK.EK
c) K là trung điểm của MB