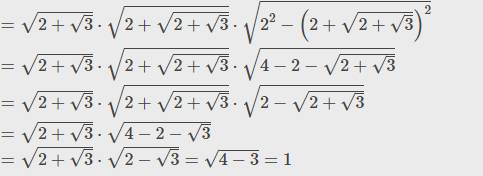A= \(\sqrt{3+2\sqrt{2}}-\sqrt{3-2\sqrt{2}}\)

Những câu hỏi liên quan
1. Thu gọn
a) A=\(\left(\sqrt{3+2\sqrt{2}}-\sqrt{3-2\sqrt{2}}\right)\left(\sqrt{3-2\sqrt{2}}+\sqrt{3+2\sqrt{2}}\right)\)
b) B=\(\sqrt{2+\sqrt{3}}.\sqrt{2+\sqrt{2+\sqrt{3}}}.\sqrt{2-\sqrt{2-\sqrt{3}}}\)
c) C=\(\dfrac{2+\sqrt{3}}{\sqrt{2}+\sqrt{2+\sqrt{3}}}+\dfrac{2-\sqrt{3}}{\sqrt{2}-\sqrt{2-\sqrt{3}}}\)
a, Ta có : \(\left\{{}\begin{matrix}\sqrt{3+2\sqrt{2}}=\sqrt{2+2\sqrt{2}+1}=\sqrt{\left(\sqrt{2}+1\right)^2}=\sqrt{2}+1\\\sqrt{3-2\sqrt{2}}=\sqrt{\left(\sqrt{2}-1\right)^2}=\sqrt{2}-1\end{matrix}\right.\)
- Thay lần lượt vào A ta được :
\(A=\left(\sqrt{2}+1-\sqrt{2}+1\right)\left(\sqrt{2}-1+\sqrt{2}+1\right)=2.2\sqrt{2}=4\sqrt{2}\)
b, \(B=\sqrt{2+\sqrt{3}}\sqrt{2^2-\left(\sqrt{2+\sqrt{3}}\right)^2}=\sqrt{2+\sqrt{3}}\sqrt{4-2-\sqrt{3}}\)
\(=\sqrt{2-\sqrt{3}}\sqrt{2+\sqrt{3}}=\sqrt{4-3}=\sqrt{1}=1\)
c, \(C=\dfrac{\left(2+\sqrt{3}\right)\left(\sqrt{2}-\sqrt{2-\sqrt{3}}\right)+\left(2-\sqrt{3}\right)\left(\sqrt{2}+\sqrt{2+\sqrt{3}}\right)}{\left(\sqrt{2}+\sqrt{2+\sqrt{3}}\right)\left(\sqrt{2}-\sqrt{2-\sqrt{3}}\right)}\)
\(=\dfrac{2\sqrt{2}+\sqrt{6}-2\sqrt{2-\sqrt{3}}-\sqrt{3}\sqrt{2-\sqrt{3}}+2\sqrt{2}-\sqrt{6}+2\sqrt{2+\sqrt{3}}-\sqrt{3}\sqrt{2+\sqrt{3}}}{\left(\sqrt{2}+\sqrt{2+\sqrt{3}}\right)\left(\sqrt{2}-\sqrt{2-\sqrt{3}}\right)}\)
\(=\dfrac{4\sqrt{2}-2\sqrt{3}\sqrt{2-\sqrt{3}}}{\left(\sqrt{2}+\sqrt{2+\sqrt{3}}\right)\left(\sqrt{2}-\sqrt{2-\sqrt{3}}\right)}\)
Đúng 1
Bình luận (0)
a) Ta có: \(A=\left(\sqrt{3+2\sqrt{2}}-\sqrt{3-2\sqrt{2}}\right)\left(\sqrt{3-2\sqrt{2}}+\sqrt{3+2\sqrt{2}}\right)\)
\(=\left(\sqrt{2}+1-\sqrt{2}+1\right)\left(\sqrt{2}-1+\sqrt{2}+1\right)\)
\(=2\cdot2\sqrt{2}=4\sqrt{2}\)
Đúng 0
Bình luận (0)
1.Chứng minh:\(\dfrac{a+\sqrt{2+\sqrt{5}.}\sqrt{\sqrt{9-4\sqrt{5}}}}{3\sqrt{2-\sqrt{5}}.\sqrt[3]{\sqrt{9+4\sqrt{5}-}3\sqrt{a^2}+\sqrt[3]{a}}}\)=\(-\sqrt[3]{a}-1\)
2.Rút gọn: \(\left(\dfrac{a^3\sqrt[]{a}-2a^3\sqrt{b}+\sqrt[3]{a^2}-\sqrt[3]{b}}{\sqrt[3]{a^2-\sqrt[3]{ab}}}+\dfrac{\sqrt[3]{a^2b}-\sqrt[3]{ab^2}}{\sqrt[3]{a}-\sqrt[3]{b}}\right)1\dfrac{1}{\sqrt[3]{a^2}}\)
Thu gọn
a) A=\(\dfrac{2\left(\sqrt{2}+\sqrt{6}\right)}{3\sqrt{2+\sqrt{3}}}\) b)B=\(\sqrt{8-2\sqrt{15}}-\sqrt{\left(3-3\sqrt{5}\right)^2}\)
c) C=\(2\sqrt{8\sqrt{3}-2\sqrt{5\sqrt{3}}-3\sqrt{20\sqrt{3}}}\)
a: \(A=\dfrac{2\sqrt{2}\left(\sqrt{3}+1\right)}{3\cdot\sqrt{2+\sqrt{3}}}=\dfrac{4\left(\sqrt{3}+1\right)}{3\cdot\sqrt{4+2\sqrt{3}}}\)
\(=\dfrac{4\left(\sqrt{3}+1\right)}{3\left(\sqrt{3}+1\right)}=\dfrac{4}{3}\)
b: \(B=\sqrt{\left(\sqrt{5}-\sqrt{3}\right)^2}-\left|3\sqrt{5}-3\right|\)
\(=\sqrt{5}-\sqrt{3}-3\sqrt{5}+3=3-\sqrt{3}-2\sqrt{5}\)
Đúng 1
Bình luận (0)
Thực hiện các phép tính :
1. \(A=\sqrt{2-\sqrt{3}}\sqrt{2+\sqrt{2-\sqrt{3}}}\sqrt{2+\sqrt{2+\sqrt{2-\sqrt{3}}}}\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2-\sqrt{3}}}}}\)
2. \(B=\left(\dfrac{1}{1+\sqrt{2}}+\dfrac{2}{2+\sqrt{3}}+...+\dfrac{1}{20+\sqrt{21}}\right)\cdot2022\)
Giải chi tiết giúp mình ạ
1:
\(A=\sqrt{2-\sqrt{3}}\cdot\sqrt{2+\sqrt{2-\sqrt{3}}}\cdot\sqrt{2^2-\left(2+\sqrt{2-\sqrt{3}}\right)}\)
\(=\sqrt{2-\sqrt{3}}\cdot\sqrt{2+\sqrt{2-\sqrt{3}}}\cdot\sqrt{2-\sqrt{2-\sqrt{3}}}\)
\(=\sqrt{2-\sqrt{3}}\cdot\sqrt{4-2+\sqrt{3}}\)
\(=\sqrt{2-\sqrt{3}}\cdot\sqrt{2+\sqrt{3}}=1\)
Đúng 0
Bình luận (0)
Tính giá trị các biểu thức sau:
a) Asqrt{frac{2+sqrt{3}}{2-sqrt{3}}}+sqrt{frac{2-sqrt{3}}{2+sqrt{3}}}
b) Afrac{sqrt{3-2sqrt{2}}}{sqrt{17-12sqrt{2}}}-frac{sqrt{3+2sqrt{2}}}{sqrt{17+12sqrt{2}}}
c) Afrac{sqrt{5}+sqrt{3}}{sqrt{5}-sqrt{3}}+frac{sqrt{5}-sqrt{3}}{sqrt{5}+sqrt{3}}
c) Afrac{sqrt{5}-sqrt{3}}{sqrt{5}+sqrt{3}}+frac{sqrt{5}+sqrt{3}}{sqrt{5}-sqrt{3}}-frac{sqrt{5}+1}{sqrt{5}-1}
Đọc tiếp
Tính giá trị các biểu thức sau:
a) \(A=\sqrt{\frac{2+\sqrt{3}}{2-\sqrt{3}}}+\sqrt{\frac{2-\sqrt{3}}{2+\sqrt{3}}}\)
b) \(A=\frac{\sqrt{3-2\sqrt{2}}}{\sqrt{17-12\sqrt{2}}}-\frac{\sqrt{3+2\sqrt{2}}}{\sqrt{17+12\sqrt{2}}}\)
c) \(A=\frac{\sqrt{5}+\sqrt{3}}{\sqrt{5}-\sqrt{3}}+\frac{\sqrt{5}-\sqrt{3}}{\sqrt{5}+\sqrt{3}}\)
c) \(A=\frac{\sqrt{5}-\sqrt{3}}{\sqrt{5}+\sqrt{3}}+\frac{\sqrt{5}+\sqrt{3}}{\sqrt{5}-\sqrt{3}}-\frac{\sqrt{5}+1}{\sqrt{5}-1}\)
a/ \(A=\frac{\sqrt{\left(2+\sqrt{3}\right)\left(2-\sqrt{3}\right)}}{2-\sqrt{3}}+\frac{\sqrt{\left(2-\sqrt{3}\right)\left(2+\sqrt{3}\right)}}{2+\sqrt{3}}\)
\(A=\frac{2+\sqrt{3}+2-\sqrt{3}}{\left(2-\sqrt{3}\right)\left(2+\sqrt{3}\right)}=\frac{4}{1}=4\)
b/\(A=\frac{\sqrt{\left(\sqrt{2}-1\right)^2}}{\sqrt{\left(3-2\sqrt{2}\right)^2}}-\frac{\sqrt{\left(\sqrt{2}+1\right)^2}}{\sqrt{\left(3+2\sqrt{2}\right)^2}}\)
\(A=\frac{\sqrt{2}-1}{3-2\sqrt{2}}-\frac{\sqrt{2}+1}{3+2\sqrt{2}}\)
\(A=\frac{\left(\sqrt{2}-1\right)\left(3+2\sqrt{2}\right)-\left(\sqrt{2}+1\right)\left(3-2\sqrt{2}\right)}{9-8}\)
\(A=3\sqrt{2}+4-3-2\sqrt{2}-3\sqrt{2}+4-3+2\sqrt{2}=8\)
c/ \(A=\frac{\left(\sqrt{5}+\sqrt{3}\right)^2+\left(\sqrt{5}-\sqrt{3}\right)^2}{5-3}\)
\(A=\frac{5+2\sqrt{15}+3+5-2\sqrt{15}+3}{2}=8\)
d/ theo câu c có \(\frac{\sqrt{5}-\sqrt{3}}{\sqrt{5}+\sqrt{3}}+\frac{\sqrt{5}+\sqrt{3}}{\sqrt{5}-\sqrt{3}}=8\)
\(\Rightarrow A=8-\frac{\left(\sqrt{5}+1\right)^2}{5-1}=\frac{32-5-2\sqrt{5}-1}{4}=\frac{2\left(13-\sqrt{5}\right)}{4}=\frac{13-\sqrt{5}}{2}\)
Đúng 0
Bình luận (1)
Cho hđt:
sqrt{apmsqrt{b}}sqrt{frac{a+sqrt{a^2-b}}{2}}pmsqrt{frac{a-sqrt{a^2-b}}{2}} (a,b0 và a^2-b0)
Áp dụng kq để rút gọn:
a.frac{2+sqrt{3}}{sqrt{2}+sqrt{2+sqrt{3}}}+frac{2-sqrt{3}}{sqrt{2}-sqrt{2-sqrt{3}}}
b. frac{sqrt{3-2sqrt{2}}}{sqrt{17-12sqrt{2}}}-frac{sqrt{3+2sqrt{2}}}{sqrt{17+12sqrt{2}}}
c. sqrt{frac{2sqrt{10}+sqrt{30}-2sqrt{2}-sqrt{6}}{2sqrt{10}-2sqrt{2}}}:frac{2}{sqrt{3}-1}
Đọc tiếp
Cho hđt:
\(\sqrt{a\pm\sqrt{b}}=\sqrt{\frac{a+\sqrt{a^2-b}}{2}}\pm\sqrt{\frac{a-\sqrt{a^2-b}}{2}}\) (a,b>0 và \(a^2-b>0\))
Áp dụng kq để rút gọn:
\(a.\frac{2+\sqrt{3}}{\sqrt{2}+\sqrt{2+\sqrt{3}}}+\frac{2-\sqrt{3}}{\sqrt{2}-\sqrt{2-\sqrt{3}}}\)
b. \(\frac{\sqrt{3-2\sqrt{2}}}{\sqrt{17-12\sqrt{2}}}-\frac{\sqrt{3+2\sqrt{2}}}{\sqrt{17+12\sqrt{2}}}\)
c. \(\sqrt{\frac{2\sqrt{10}+\sqrt{30}-2\sqrt{2}-\sqrt{6}}{2\sqrt{10}-2\sqrt{2}}}:\frac{2}{\sqrt{3}-1}\)
Tính ;
a) sqrt{4+sqrt{8}}.sqrt{2+sqrt{2+sqrt{2}}.}sqrt{2-sqrt{2+sqrt{2}}}
b) sqrt{47+sqrt{5}}.sqrt{7-sqrt{2+sqrt{5}}}.sqrt{7+sqrt{2+sqrt{5}}}
c) sqrt{2+sqrt{3}}.sqrt{2+sqrt{2+sqrt{3}}}.sqrt{2+sqrt{2+sqrt{2+sqrt{3}}}}.sqrt{2-sqrt{2+sqrt{2+sqrt{3}}}}
d) sqrt{31+sqrt{2}}.sqrt{6+sqrt{5+sqrt{2}}}sqrt{3+sqrt{3+sqrt{5+sqrt{2}}}}.sqrt{3-sqrt{3+sqrt{5+sqrt{2}}}}
Đọc tiếp
Tính ;
a) \(\sqrt{4+\sqrt{8}}.\sqrt{2+\sqrt{2+\sqrt{2}}.}\sqrt{2-\sqrt{2+\sqrt{2}}}\)
b) \(\sqrt{47+\sqrt{5}}.\sqrt{7-\sqrt{2+\sqrt{5}}}.\sqrt{7+\sqrt{2+\sqrt{5}}}\)
c) \(\sqrt{2+\sqrt{3}}.\sqrt{2+\sqrt{2+\sqrt{3}}}.\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{3}}}}.\sqrt{2-\sqrt{2+\sqrt{2+\sqrt{3}}}}\)
d) \(\sqrt{31+\sqrt{2}}.\sqrt{6+\sqrt{5+\sqrt{2}}}\sqrt{3+\sqrt{3+\sqrt{5+\sqrt{2}}}}.\sqrt{3-\sqrt{3+\sqrt{5+\sqrt{2}}}}\)
Tính giá trị biểu thức
A = \(\frac{\sqrt{45+27\sqrt{2}}+\sqrt{45-27\sqrt{2}}}{\sqrt{5+3\sqrt{2}}-\sqrt{5-3\sqrt{2}}}-\frac{\sqrt{3+\sqrt{2}}+\sqrt{3-\sqrt{2}}}{\sqrt{3+\sqrt{2}}-\sqrt{3-\sqrt{2}}}\)
B = \(\frac{1}{\sqrt{2}-\sqrt{3}}\cdot\sqrt{\frac{3\sqrt{2}-2\sqrt{3}}{3\sqrt{2}+2\sqrt{3}}}\)
Rút gọn
\(A=\sqrt{2+\sqrt{3}}.\sqrt{2+\sqrt{2+\sqrt{3}}}.\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{3}}}}.\sqrt{2-\sqrt{2+\sqrt{2+\sqrt{3}}}}\)
rút gọn A =\(\frac{\sqrt{45+27\sqrt{2}}+\sqrt{45-27\sqrt{2}}}{\sqrt{5+3\sqrt{2}}-\sqrt{5-3\sqrt{2}}}-\frac{\sqrt{3+\sqrt{2}}+\sqrt{3-\sqrt{2}}}{\sqrt{3+\sqrt{2}}-\sqrt{3-\sqrt{2}}}\)
Ta có: \(A=\frac{\sqrt{45+27\sqrt{2}}+\sqrt{45-27\sqrt{2}}}{\sqrt{5+3\sqrt{2}}-\sqrt{5-3\sqrt{2}}}-\frac{\sqrt{3+\sqrt{2}}+\sqrt{3-\sqrt{2}}}{\sqrt{3+\sqrt{2}}-\sqrt{3-\sqrt{2}}}\)
\(=\frac{3\left(\sqrt{5+3\sqrt{2}}+\sqrt{5-3\sqrt{2}}\right)^2}{\left(\sqrt{5+3\sqrt{2}}\right)^2-\left(\sqrt{5-3\sqrt{2}}\right)^2}-\frac{\left(\sqrt{3+\sqrt{2}}+\sqrt{3-\sqrt{2}}\right)^2}{\left(\sqrt{3+\sqrt{2}}\right)^2-\left(\sqrt{3-\sqrt{2}}\right)^2}\)
\(=\frac{3\left[\left(\sqrt{5+3\sqrt{2}}\right)^2+2\cdot\sqrt{5+3\sqrt{2}}\cdot\sqrt{5-3\sqrt{2}}+\left(\sqrt{5-3\sqrt{2}}\right)^2\right]}{\left|5+3\sqrt{2}\right|-\left|5-3\sqrt{2}\right|}-\frac{\left(\sqrt{3+\sqrt{2}}\right)^2+2\cdot\sqrt{3+\sqrt{2}}\cdot\sqrt{3-\sqrt{2}}+\left(\sqrt{3-\sqrt{2}}\right)^2}{\left|3+\sqrt{2}\right|-\left|3-\sqrt{2}\right|}\)
\(=\frac{3\left(\left|5+3\sqrt{2}\right|+2\sqrt{7}+\left|5-3\sqrt{2}\right|\right)}{5+3\sqrt{2}-\left(5-3\sqrt{2}\right)}-\frac{\left|3+\sqrt{2}\right|+2\cdot\sqrt{7}+\left|3-\sqrt{2}\right|}{3+\sqrt{2}-\left(3-\sqrt{2}\right)}\)
\(=\frac{3\left(5+3\sqrt{2}+2\sqrt{7}+5-3\sqrt{2}\right)}{5+3\sqrt{2}-5+3\sqrt{2}}-\frac{3+\sqrt{2}+2\sqrt{7}+3-\sqrt{2}}{3+\sqrt{2}-3+\sqrt{2}}\)
\(=\frac{3\left(10+2\sqrt{7}\right)}{6\sqrt{2}}-\frac{6+2\sqrt{7}}{2\sqrt{2}}\)
\(=\frac{3\left(10+2\sqrt{7}\right)}{6\sqrt{2}}-\frac{3\left(6+2\sqrt{7}\right)}{6\sqrt{2}}\)
\(=\frac{30+6\sqrt{7}-18-6\sqrt{7}}{6\sqrt{2}}\)
\(=\frac{12}{6\sqrt{2}}=\sqrt{2}\)
Vậy: \(A=\sqrt{2}\)
Đúng 0
Bình luận (0)