10+45-6+3x2=?

Những câu hỏi liên quan
lựa chọn các dấu ngoặc (neu cần )rồi đặt vào vi trí thích hợp để được kết quả đúng:
6+2X4-3X2=10
6+2X4-3X2=16
6+2X4-3X2=26
6+2X4-3X2=8
6 + 2 * ( 4 - 3 ) * 2 = 10
6 + ( 2 * 4 - 3 ) * 2 = 16
( 6 + 2 ) * 4 - 3 * 2 = 26
6 + ( 2 * 4 - 3 * 2 ) = 8
Đúng 0
Bình luận (0)
Tìm x
a)3x2-6x=0
b)x.(x-6)+10(x-6)=0
c) (x+2)2 =x+2
a, \(\Leftrightarrow3x\left(x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}3x=0\\x-2=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
Vậy ...
b, \(\Leftrightarrow\left(x-6\right)\left(x+10\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-6=0\\x+10=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=6\\x=-10\end{matrix}\right.\)
Vậy ...
c, \(\Leftrightarrow\left(x+2\right)^2-\left(x+2\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left(x+2-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+2=0\\x+1=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=-1\end{matrix}\right.\)
Vậy ...
Đúng 3
Bình luận (0)
\(a.\)
\(3x^2-6x=0\)
\(\Leftrightarrow3x\cdot\left(x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}3x=0\\x-2=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
\(b.\)
\(x\cdot\left(x-6\right)+10\cdot\left(x-6\right)=0\)
\(\Leftrightarrow\left(x-6\right)\cdot\left(x+10\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-6=0\\x+10=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=6\\x=-10\end{matrix}\right.\)
\(c.\)
\(\left(x+2\right)^2=x+2\)
\(\Leftrightarrow x^2+4x+4-x-2=0\)
\(\Leftrightarrow x^2+3x+2=0\)
\(\Leftrightarrow\left(x+1\right)\cdot\left(x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+1=0\\x+2=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=-2\end{matrix}\right.\)
Đúng 2
Bình luận (0)
Giải phương trình bằng cách đưa về phương trình tích:
a
)
3
x
2
−
7
x
−
10
⋅
2
x
2...
Đọc tiếp
Giải phương trình bằng cách đưa về phương trình tích:
a ) 3 x 2 − 7 x − 10 ⋅ 2 x 2 + ( 1 − 5 ) x + 5 − 3 = 0 b ) x 3 + 3 x 2 − 2 x − 6 = 0 c ) x 2 − 1 ( 0 , 6 x + 1 ) = 0 , 6 x 2 + x d ) x 2 + 2 x − 5 2 = x 2 − x + 5 2
a) 3 x 2 − 7 x − 10 ⋅ 2 x 2 + ( 1 − 5 ) x + 5 − 3 = 0
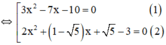
+ Giải (1):
3 x 2 – 7 x – 10 = 0
Có a = 3; b = -7; c = -10
⇒ a – b + c = 0
⇒ (1) có hai nghiệm x 1 = - 1 v à x 2 = - c / a = 10 / 3 .
+ Giải (2):
2 x 2 + ( 1 - √ 5 ) x + √ 5 - 3 = 0
Có a = 2; b = 1 - √5; c = √5 - 3
⇒ a + b + c = 0
⇒ (2) có hai nghiệm:
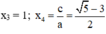
Vậy phương trình có tập nghiệm 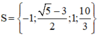
b)
x 3 + 3 x 2 - 2 x - 6 = 0 ⇔ x 3 + 3 x 2 - ( 2 x + 6 ) = 0 ⇔ x 2 ( x + 3 ) - 2 ( x + 3 ) = 0 ⇔ x 2 - 2 ( x + 3 ) = 0
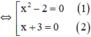
+ Giải (1): x 2 – 2 = 0 ⇔ x 2 = 2 ⇔ x = √2 hoặc x = -√2.
+ Giải (2): x + 3 = 0 ⇔ x = -3.
Vậy phương trình có tập nghiệm S = {-3; -√2; √2}
c)
x 2 − 1 ( 0 , 6 x + 1 ) = 0 , 6 x 2 + x ⇔ x 2 − 1 ( 0 , 6 x + 1 ) = x ⋅ ( 0 , 6 x + 1 ) ⇔ x 2 − 1 ( 0 , 6 x + 1 ) − x ( 0 , 6 x + 1 ) = 0 ⇔ ( 0 , 6 x + 1 ) x 2 − 1 − x = 0
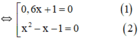
+ Giải (1): 0,6x + 1 = 0 ⇔ 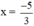
+ Giải (2):
x 2 – x – 1 = 0
Có a = 1; b = -1; c = -1
⇒ Δ = ( - 1 ) 2 – 4 . 1 . ( - 1 ) = 5 > 0
⇒ (2) có hai nghiệm 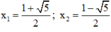
Vậy phương trình có tập nghiệm 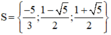
d)
x 2 + 2 x − 5 2 = x 2 − x + 5 2 ⇔ x 2 + 2 x − 5 2 − x 2 − x + 5 2 = 0 ⇔ x 2 + 2 x − 5 − x 2 − x + 5 ⋅ x 2 + 2 x − 5 + x 2 − x + 5 = 0 ⇔ ( 3 x − 10 ) 2 x 2 + x = 0
⇔ (3x-10).x.(2x+1)=0
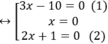
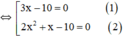
+ Giải (1): 3x – 10 = 0 ⇔ 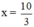
+ Giải (2):
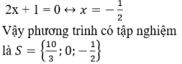
Đúng 0
Bình luận (0)
Phân tích đa thức thành nhân tử : 4(x + 5)(x + 6)(x + 10)(x + 12) + 3x2
Đa thức này không phân tích được thành nhân tử.
Bạn coi lại đề.
Đúng 0
Bình luận (0)
Ta có: \(4\left(x+5\right)\left(x+6\right)\left(x+10\right)\left(x+12\right)+3x^2\)
\(=4\left(x^2+60+17x\right)\left(x^2+60x+16x\right)+3x^2\)
\(=4\left[\left(x^2+60\right)^2+33x\left(x^2+60\right)+272x^2\right]+3x^2\)
\(=4\left(x^2+60\right)^2+132x\left(x^2+60\right)+1091x^2\)
Đúng 0
Bình luận (0)
6/5-1/3x2/5
3/8:3/4-1/4
10/7-2/5:1/3
= 6/5 - 2/15 = 16/15
= 1/2 - 1/4 = 1/4
= 10/7 - 6/5 = 8/35
Đúng 1
Bình luận (0)
6/5 - 1/3 x 2/5
= 6/5 - 2/15
= 16/15
________________________________________________
3/8 : 3/4 - 1/4
= 1/2 - 1/4
= 1/4
________________________________________________
10/7 - 2/5 : 1/3
= 10/7 - 6/5
= 8/35
Đúng 0
Bình luận (0)
lựa chọn dấu ngoặc thích hợp để được kết quả đúng:
6+2x4-3x2=10
Bài 6: Giải các phương trình sau:2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) x2 – 2x + 1 015) 1 + 3x + 3x2 + x3 0
Đọc tiếp
Bài 6: Giải các phương trình sau:
2) |
3) |
4) |
5) |
6) |
7) |
8)
9)
10)
11)
12)
13)
14) x2 – 2x + 1 = 0
15) 1 + 3x + 3x2 + x3 = 0
4) Ta có: \(\dfrac{2x-5}{5}-\dfrac{x+3}{3}=\dfrac{2-3x}{2}-x-2\)
\(\Leftrightarrow\dfrac{6\left(2x-5\right)}{30}-\dfrac{10\left(x+3\right)}{30}=\dfrac{15\left(2-3x\right)}{30}-\dfrac{30\left(x+2\right)}{30}\)
\(\Leftrightarrow12x-30-10x-30=30-45x-30x-60\)
\(\Leftrightarrow-22x-60=-75x-30\)
\(\Leftrightarrow-22x+75x=-30+60\)
\(\Leftrightarrow53x=30\)
\(\Leftrightarrow x=\dfrac{30}{53}\)
Vậy: \(S=\left\{\dfrac{30}{53}\right\}\)
5) Ta có: \(\dfrac{5x-3}{6}-\dfrac{7x-1}{4}=5\)
\(\Leftrightarrow\dfrac{2\left(5x-3\right)}{12}-\dfrac{3\left(7x-1\right)}{12}=\dfrac{60}{12}\)
\(\Leftrightarrow10x-6-21x+3=60\)
\(\Leftrightarrow-11x-3=60\)
\(\Leftrightarrow-11x=63\)
\(\Leftrightarrow x=-\dfrac{63}{11}\)
Vậy: \(S=\left\{-\dfrac{63}{11}\right\}\)
Đúng 1
Bình luận (1)
`9,x^3+x^2-2=0`
`x^3-x^2+2x^2-2=0`
`<=>x^2(x-1)+2(x-1)(x+1)=0`
`<=>(x-1)(x^2+2x+2)=0`
`<=>x=1`
`14,x^2-2x+1=0`
`<=>(x-1)^2=0`
`<=>x-1=0`
`<=>x=1`
`15,x^3+3x^2+3x+1=0`
`<=>(x+1)^3=0`
`<=>x+1=0`
`<=>x=-1`
Đúng 2
Bình luận (0)
Bài 6: Giải các phương trình sau:1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) x2 – 2x + 1 015) 1 + 3x + 3x2 + x3 0
Đọc tiếp
Bài 6: Giải các phương trình sau:
1) |
2) |
3) |
4) |
5) |
6) |
7) |
8)
9)
10)
11)
12)
13)
14) x2 – 2x + 1 = 0
15) 1 + 3x + 3x2 + x3 = 0
Bài 6:
1) Ta có: \(2x\left(x-5\right)-\left(x+3\right)^2=3x-x\left(5-x\right)\)
\(\Leftrightarrow2x^2-10x-\left(x^2+6x+9\right)=3x-5x+x^2\)
\(\Leftrightarrow2x^2-10x-x^2-6x-9-3x+5x-x^2=0\)
\(\Leftrightarrow-14x-9=0\)
\(\Leftrightarrow-14x=9\)
\(\Leftrightarrow x=-\dfrac{9}{14}\)
Vậy: \(S=\left\{-\dfrac{9}{14}\right\}\)
Đúng 5
Bình luận (0)
`1)2x(x-5)-(x+3)^2=3x-x(5-x)`
`<=>2x^2-10x-x^2-6x-9=3x-5x+x^2`
`<=>x^2-16x-9=x^2-2x`
`<=>14x=-9`
`<=>x=-9/14`
Đúng 3
Bình luận (0)
1)Rút gọn bt
a)3x2(x+1)(x-1)-(x2-1)(x4+x2+1)+(x2-1)3
b)(x+y+z)3+(x-y-z)3+(y-x-z)3+(z-y-x)3
2)Phân tích đa thức thành nhân tử:
(x-1)(x+2)(x+3)(x+6)-6(x2+5x)2+45
1)
a) \(=3x^2\left(x^2-1\right)-\left(x^3-1\right)+x^8-3x^4+3x^2-1\)
\(=3x^4-3x^2-x^3+1+x^8-3x^4+3x^2-1=x^8-x^3\)
2)
\(=\left(x^2+5x-6\right)\left(x^2+5x+6\right)-6\left(x^2+5x\right)+45\)
\(=\left(x^2+5x\right)^2-6\left(x^2+5x\right)-36+45\)
\(=\left(x^2+5x\right)^2-6\left(x^2+5x\right)+9=\left(x^2+5x-3\right)^2\)
Đúng 0
Bình luận (0)























