xét dấu f(x)=\(\frac{x^3-6x+4}{x^2-3x+2}\)

Những câu hỏi liên quan
Xét các dấu biểu thức : a) f(x) = (3-x)(x+2) b) f(x) = (x-1)(x^2-6x-7) c) f(x) = -3x^2 + x + 2
Xét dấu của mỗi tam thức bậc hai sau:
a) \(f\left( x \right) = 3{x^2} - 4x + 1\)
b) \(f\left( x \right) = 9{x^2} + 6x + 1\)
c) \(f\left( x \right) = 2{x^2} - 3x + 10\)
d) \(f\left( x \right) = - 5{x^2} + 2x + 3\)
e) \(f\left( x \right) = - 4{x^2} + 8x - 4\)
g) \(f\left( x \right) = - 3{x^2} + 3x - 1\)
a) Ta có \(a = 3 > 0,b = - 4,c = 1\)
\(\Delta ' = {\left( { - 2} \right)^2} - 3.1 = 1 > 0\)
\( \Rightarrow \)\(f\left( x \right)\) có 2 nghiệm \(x = \frac{1}{3},x = 1\). Khi đó:
\(f\left( x \right) > 0\) với mọi x thuộc các khoảng \(\left( { - \infty ;\frac{1}{3}} \right)\) và \(\left( {1; + \infty } \right)\);
\(f\left( x \right) < 0\) với mọi x thuộc các khoảng \(\left( {\frac{1}{3};1} \right)\)
b) Ta có \(a = 9 > 0,b = 6,c = 1\)
\(\Delta ' = 0\)
\( \Rightarrow \)\(f\left( x \right)\) có 1 nghiệm \(x = - \frac{1}{3}\). Khi đó:
\(f\left( x \right) > 0\) với mọi \(x \in \mathbb{R}\backslash \left\{ { - \frac{1}{3}} \right\}\)
c) Ta có \(a = 2 > 0,b = - 3,c = 10\)
\(\Delta = {\left( { - 3} \right)^2} - 4.2.10 = - 71 < 0\)
\( \Rightarrow \)\(f\left( x \right) > 0\forall x \in \mathbb{R}\)
d) Ta có \(a = - 5 < 0,b = 2,c = 3\)
\(\Delta ' = {1^2} - \left( { - 5} \right).3 = 16 > 0\)
\( \Rightarrow \)\(f\left( x \right)\) có 2 nghiệm \(x = \frac{{ - 3}}{5},x = 1\). Khi đó:
\(f\left( x \right) < 0\) với mọi x thuộc các khoảng \(\left( { - \infty ; - \frac{3}{5}} \right)\) và \(\left( {1; + \infty } \right)\);
\(f\left( x \right) > 0\) với mọi x thuộc các khoảng \(\left( { - \frac{3}{5};1} \right)\)
e) Ta có \(a = - 4 < 0,b = 8c = - 4\)
\(\Delta ' = 0\)
\( \Rightarrow \)\(f\left( x \right)\) có 1 nghiệm \(x = 1\). Khi đó:
\(f\left( x \right) < 0\) với mọi \(x \in \mathbb{R}\backslash \left\{ 1 \right\}\)
g) Ta có \(a = - 3 < 0,b = 3,c = - 1\)
\(\Delta = {3^2} - 4.\left( { - 3} \right).\left( { - 1} \right) = - 3 < 0\)
\( \Rightarrow \)\(f\left( x \right) < 0\forall x \in \mathbb{R}\)
Đúng 0
Bình luận (0)
Xét dấu các biểu thức sau:
a/ y= f(x) = ( x2 + 6x - 5)(2x2 + 2x - 5)
b/y = f(x) = \(\frac{-3x^2+7x-4}{x^2-5x+6}\)
c/ y= f(x) = x3- 6x -9
d/ y= f(x) = \(\frac{x^3-6x+4}{x^2-3x+2}\)
giúp em với ạ, em cần gấp lắm ạ
xét dấu các biểu thức sau
a) \(\frac{x^2}{3x-8}\ge1\)
b) \(\frac{x^2-3x+24}{x^2-3x+3}
nhiều quá bạn ơi , bạn k biết câu nào mình giải zúp cho
Đúng 0
Bình luận (0)
hết luôn đó bạn Ngọc Vi ... nhưng bạn giúp được câu nào thì mình cảm ơn
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Xét dấu các biểu thức sau:
a) f(x)= (x-2).(x+1)/3x -1
b) f(x)= 1-4x /2x-3
c) f(x)= 3x (6 -2x)/5x-4
d) f(x)= -4/3x+1 - 3/2-x
e) f(x)= 2x-5/(3x+1) (2-4x)
Xem chi tiết
Xét dấu: f(x)=(x^2-1)(4-3x-x^2)
\(f\left(x\right)=\left(x-1\right)\left(x+1\right)\left(1-x\right)\left(x+4\right)=-\left(x-1\right)^2\left(x+1\right)\left(x+4\right)\)
Bảng xét dấu:
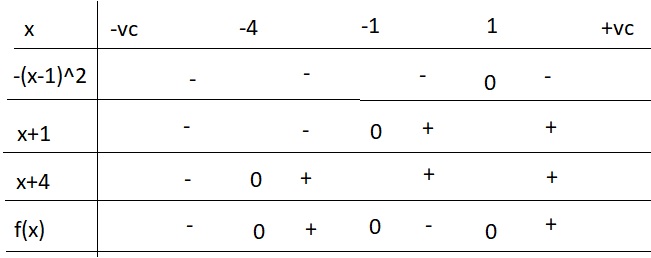
Từ bảng xét dấu trên em tự kết luận dấu của \(f\left(x\right)\)
Đúng 2
Bình luận (0)
Bài 3 : Xét dấu biểu thức sau :
1 , fleft(xright)frac{x-7}{4x^2-19x+12}
2 , fleft(xright)frac{11x+3}{-x^2+5x-7}
3 , fleft(xright)frac{3x-2}{x^3-3x^2+2}
4 , fleft(xright)frac{x^2+4x-12}{sqrt{6}x^2+3x+sqrt{2}}
5 , fleft(xright)frac{x^2-3x-2}{-x^2+x-1}
6 , fleft(xright)frac{x^3-5x+4}{x^4-4x^3+8x-5}
7 , fleft(xright)frac{left(x+3right)left(x-2right)left(-2x^2+x-1right)}{left(2x-5right)left(x^2+3x-10right)}
8 , fleft(xright)left(-x^2+x-1right)left(6x^2-5x+1right)
9 , fleft(xright)frac{x^2-...
Đọc tiếp
Bài 3 : Xét dấu biểu thức sau :
1 , \(f\left(x\right)=\frac{x-7}{4x^2-19x+12}\)
2 , \(f\left(x\right)=\frac{11x+3}{-x^2+5x-7}\)
3 , \(f\left(x\right)=\frac{3x-2}{x^3-3x^2+2}\)
4 , \(f\left(x\right)=\frac{x^2+4x-12}{\sqrt{6}x^2+3x+\sqrt{2}}\)
5 , \(f\left(x\right)=\frac{x^2-3x-2}{-x^2+x-1}\)
6 , \(f\left(x\right)=\frac{x^3-5x+4}{x^4-4x^3+8x-5}\)
7 , \(f\left(x\right)=\frac{\left(x+3\right)\left(x-2\right)\left(-2x^2+x-1\right)}{\left(2x-5\right)\left(x^2+3x-10\right)}\)
8 , \(f\left(x\right)=\left(-x^2+x-1\right)\left(6x^2-5x+1\right)\)
9 , \(f\left(x\right)=\frac{x^2-x-2}{-x^2+3x+4}\)
10 , \(f\left(x\right)=\left(x^2-5x+4\right)\left(2-5x+2x^2\right)\)
1.
\(f\left(x\right)=\frac{x-7}{\left(x-4\right)\left(4x-3\right)}\)
Vậy:
\(f\left(x\right)\) ko xác định tại \(x=\left\{\frac{3}{4};4\right\}\)
\(f\left(x\right)=0\Rightarrow x=7\)
\(f\left(x\right)>0\Rightarrow\left[{}\begin{matrix}\frac{3}{4}< x< 4\\x>7\end{matrix}\right.\)
\(f\left(x\right)< 0\Rightarrow\left[{}\begin{matrix}x< \frac{3}{4}\\4< x< 7\end{matrix}\right.\)
2.
\(f\left(x\right)=\frac{11x+3}{-\left(x-\frac{5}{2}\right)^2-\frac{3}{4}}\)
Vậy:
\(f\left(x\right)=0\Rightarrow x=-\frac{3}{11}\)
\(f\left(x\right)>0\Rightarrow x< -\frac{3}{11}\)
\(f\left(x\right)< 0\Rightarrow x>-\frac{3}{11}\)
3.
\(f\left(x\right)=\frac{3x-2}{\left(x-1\right)\left(x^2-2x-2\right)}\)
Vậy:
\(f\left(x\right)\) ko xác định khi \(x=\left\{1;1\pm\sqrt{3}\right\}\)
\(f\left(x\right)=0\Rightarrow x=\frac{2}{3}\)
\(f\left(x\right)>0\Rightarrow\left[{}\begin{matrix}x< 1-\sqrt{3}\\\frac{2}{3}< x< 1\\x>1+\sqrt{3}\end{matrix}\right.\)
\(f\left(x\right)< 0\Rightarrow\left[{}\begin{matrix}1-\sqrt{3}< x< \frac{2}{3}\\1< x< 1+\sqrt{3}\end{matrix}\right.\)
4.
\(f\left(x\right)=\frac{\left(x-2\right)\left(x+6\right)}{\sqrt{6}\left(x+\frac{\sqrt{6}}{4}\right)^2+\frac{8\sqrt{2}-3\sqrt{6}}{8}}\)
Vậy:
\(f\left(x\right)=0\Rightarrow x=\left\{-6;2\right\}\)
\(f\left(x\right)>0\Rightarrow\left[{}\begin{matrix}x< -6\\x>2\end{matrix}\right.\)
\(f\left(x\right)< 0\Rightarrow-6< x< 2\)
5.
\(f\left(x\right)=\frac{x^2-3x-2}{-\left(x-\frac{1}{2}\right)^2-\frac{3}{4}}\)
Vậy:
\(f\left(x\right)=0\Rightarrow x=\frac{3\pm\sqrt{17}}{2}\)
\(f\left(x\right)>0\Rightarrow\frac{3-\sqrt{17}}{2}< x< \frac{3+\sqrt{17}}{2}\)
\(f\left(x\right)< 0\Rightarrow\left[{}\begin{matrix}x< \frac{3-\sqrt{17}}{2}\\x>\frac{3+\sqrt{17}}{2}\end{matrix}\right.\)
6.
\(f\left(x\right)=\frac{\left(x-1\right)\left(x^2+x-4\right)}{\left(x-1\right)^2\left(x^2-2x-5\right)}=\frac{x^2+x-4}{\left(x-1\right)\left(x^2-2x-5\right)}\)
Vậy:
\(f\left(x\right)\) ko xác định khi \(x=\left\{1;1\pm\sqrt{6}\right\}\)
\(f\left(x\right)=0\Rightarrow x=\left\{\frac{-1\pm\sqrt{17}}{2}\right\}\)
\(f\left(x\right)>0\Rightarrow\left[{}\begin{matrix}\frac{-1-\sqrt{17}}{2}< x< 1-\sqrt{6}\\1< x< \frac{-1+\sqrt{17}}{2}\\x>1+\sqrt{6}\end{matrix}\right.\)
\(f\left(x\right)< 0\Rightarrow\left[{}\begin{matrix}x< \frac{-1-\sqrt{17}}{2}\\1-\sqrt{6}< x< 1\\\frac{-1+\sqrt{17}}{2}< x< 1+\sqrt{6}\end{matrix}\right.\)
Xem thêm câu trả lời
Xét dấu các biểu thức tích, thương các tam thức bậc hai
a. \(f\left(x\right)=x^2\left(2-x-x^2\right)\left(x+2\right)\)
b. \(f\left(x\right)=\frac{x^4-3x^3+2x^2}{x^2-x-30}\)
a) F(x) = \(-x^2\left(x-1\right)\left(x+2\right)\left(x+2\right)=\left(1-x\right)x^2\left(x+2\right)^2\\ \)
\(\left\{{}\begin{matrix}x^2\ge0\\\left(x+2\right)^2\ge0\end{matrix}\right.\) => dấu biểu thức chỉ phụ thuộc vào thừa số (1-x)
F(x) =0 khi x={-2,0,1}
F(x) > 0 khi x<1 và khác -2 và 0
f(x) <0 khi x> 1
Đúng 0
Bình luận (0)
Tử f(x) =x^2(x^2-3x+2) =x^2(x-1)(x-2)
tương tự a) dấu của tử phụ thuộc (x-1)(x-2)
Mẫu f(x) =x^2 -x-30 =(x-5)(x+6)
Phần hỗ trợ Lập bảng đây khó thao tác
=> viết bằng hệ {điểm tới hạn xet x={-6,0,1,2,5}
Khi => \(\left[{}\begin{matrix}x=0\\x=1\\x=2\end{matrix}\right.\)=>f(x) =0
Khi \(\left[{}\begin{matrix}x=5\\x=-6\end{matrix}\right.\) => f(x) không xác định
Khi \(x< -6\Rightarrow\left\{{}\begin{matrix}Tf\left(x\right)>0\\Mf\left(x\right)>0\end{matrix}\right.\)\(\Rightarrow f\left(x\right)>0\)
khi -6<x<1 \(\Rightarrow\left\{{}\begin{matrix}Tf\left(x\right)>0\\Mf\left(x\right)< 0\end{matrix}\right.\) => f(x) <0
khi 1<x<2 \(\Rightarrow\left\{{}\begin{matrix}Tf\left(x\right)< 0\\Mf\left(x\right)< 0\end{matrix}\right.\) => f(x) >0
khi 2<x<5 \(\Rightarrow\left\{{}\begin{matrix}Tf\left(x\right)>0\\Mf\left(x\right)< 0\end{matrix}\right.\) => f(x) <0
khi x>5 \(\Rightarrow\left\{{}\begin{matrix}Tf\left(x\right)>0\\Mf\left(x\right)>0\end{matrix}\right.\) => f(x) >0
Đúng 0
Bình luận (0)
Lập bảng xét dấu :
\(f\left(x\right)=\frac{x^2-3x+2}{-x^2+x+12^{ }}\)
Đặt TT: = \(x^2+3x+2;MT:=-x^2+x+12\)
Lập bảng xét dấu TT và MT trên tập xác đinh D=R/\(\left\{-3;4\right\}\)
Từ đó suy ra dấu của f(x)
| x | -\(\infty\) -3 1 2 4 \(+\infty\) |
| TT | + + 0 - 0 + + |
| MT | - 0 + + + 0 - |
| f(x) | - // + 0 - 0 + // - |
Từ bảng xét dấu ta được
\(T\left(f\left(x\right)=0\right)=\left\{1;2\right\}\) ; \(T\left(f\left(x\right)\ne0\right)=R\) / \(\left\{-3;1;2;4\right\}\)
\(T\left(f\left(x\right)>0\right)=\left(3;1\right)\cup\left(2;4\right)\) ; \(T\left(f\left(x\right)\ge0\right)=\left(-3;1\right)\cup\left(2;4\right)\)
\(T\left(f\left(x\right)<0\right)=\left(-\infty;-3\right)\cup\left(1;2\right)\cup\left(4;+\infty\right)\)
\(T\left(f\left(x\right)\le0\right)=\left(-\infty;-3\right)\cup\left[1;2\right]\cup\left(4;+\infty\right)\)
Đúng 0
Bình luận (0)














