Cho ABC
vuông tại A, có AB = 6cm, AC = 8cm, C = 37độ.
Tính BC, B
Những câu hỏi liên quan
cho tam giác abc vuông tại A có AB = 6cm AC = 8cm a) tính BC b) tia phân giác của góc ABC cắt AC tại K kẻ KH vuông BC tại H
a: BC=10cm
b: Xét ΔABK vuông tại A và ΔHBK vuông tại H có
BK chung
\(\widehat{ABK}=\widehat{HBK}\)
Do đó: ΔABK=ΔHBK
Đúng 0
Bình luận (0)
1. Cho ABC vuông tại A, biết AB = 6cm, góc B = 60∘ . Tính AC, BC.
2. Cho ABC vuông tại A, biết AB = 8cm, góc C = 30∘ . Tính BC, AC.
3. Cho DBC vuông tại D, biết BC = 10cm, góc C = 45∘. Tính BD, DC.
4. Cho ABC vuông tại A có:
a) C= 60 , BC =16. Tính AB, AC.
b)B =45 , BC =5√ 2 . Tính AB, AC.
Cho ABC
vuông tại A, có AB = 6cm, AC = 8cm, C = 37 0 .
Tính BC, B
*) Áp dụng định lý Pytago vào tam giác ABC vuông tại A có:
AB2+AC2=BC2
Thay AB=6cm, AC=8cm
=> 62+82=BC2
<=> 100=BC2
<=> BC=10 cm (BC>0)
*) Xét tam giác ABC vuông tại A có: \(\hept{\begin{cases}\widehat{BAC}=90^o\\\widehat{C}=37^o\end{cases}}\)
\(\Rightarrow37^o+\widehat{B}+90^o=180^o\)
\(\Leftrightarrow\widehat{B}=53^o\)
cho tam giac abc vuông tại a, AB 3cm bc 5 cm so sánh góc b và c
Cho tam giác ABC có AB=6cm, AC=8cm, tia phân giác góc A cắt BC tại D. CMR: góc ADB<góc ADC.
Cho tam giác ABC cân tại A có chu vi = 20cm.Cạnh y của BC=6cm. So sánh các góc của ABC?
Bài 1:
AC=4cm
Xét ΔABC có AB<AC
nên \(\widehat{C}< \widehat{B}\)
Bài 2:
BC=6cm
=>AB+AC=14cm
mà AB=AC
nên AB=AC=7cm
Xét ΔABC có AB=AC>BC
nên \(\widehat{B}=\widehat{C}>\widehat{A}\)
Đúng 0
Bình luận (0)
cho ABC có AB=6cm AC = 8cm vuông tại A a ) tính BC b) vẽ tia phân giác BD của góc B ( D thuộc AC ), từ D vẽ DE vuông góc với BC (E thuộc BC ) chứng minh tam giác ABC = tam giác EBD . c ) ED cắt AB tại F chúng minh tam giác ABC =tam giác EBF
a: BC=10cm
b: Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó; ΔABD=ΔEBD
Đúng 0
Bình luận (0)
Cho tam giác abc có AB=6cm;AC=8cm;Bc=10cm. chứng tỏ tam giác ABC vuông tại A,Tia phân giác của góc B cắt AC tại D, kẻ DE vuông góc với BC tại E
a) Ta có:
\(BC^2=AB^2+AC^2\)
\(10^2=6^2+8^2=36+64=100\)
Áp dụng định lí Pytago đảo
⇒ Tam giác ABC vuông tại A
b) 1/ Xét tam giác ABD và tam giác EBD có
^A=^E=90o(gt)
BD: cạnh chung
^B1=^B2(BD phân giác ^B)
⇒ Tam giác ABD= tam giác EBD
2/ Em xem lại đề ha
Đúng 3
Bình luận (0)
Tam giác ABC vuông tại A có AB= 6cm AC= 8cm Khi đó BC =
A. 7cm B. 2cm C. 14cm D.10cm
Theo định lí Pytago tam giác ABC vuông tại A
\(BC=\sqrt{AB^2+AC^2}=10cm\)
chọn D
Đúng 4
Bình luận (0)
Áp dụng định lí Pytago ta có
\(BC^2=AB^2+AC^2\\ =\sqrt{6^2+8^2}=\sqrt{36+64}=10\\ \Rightarrow D\)
Đúng 5
Bình luận (0)
Xem thêm câu trả lời
Cho ∆abc vuông tại a có ab=6cm, ac=8cm. Tia phân giác của góc abc cắt ac tại d.
a)Tính bc
b) Kẻ ah vuông góc với bc, tia ah cắt bc tại k. Chứng minh:∆ahb=∆khb
c) Chứng minh:dk vuông góc với bc
d) Qua c kẻ đường thẳng song song với ak, cắt tia ba tại e. Chứng minh:2(ad+ae)>ec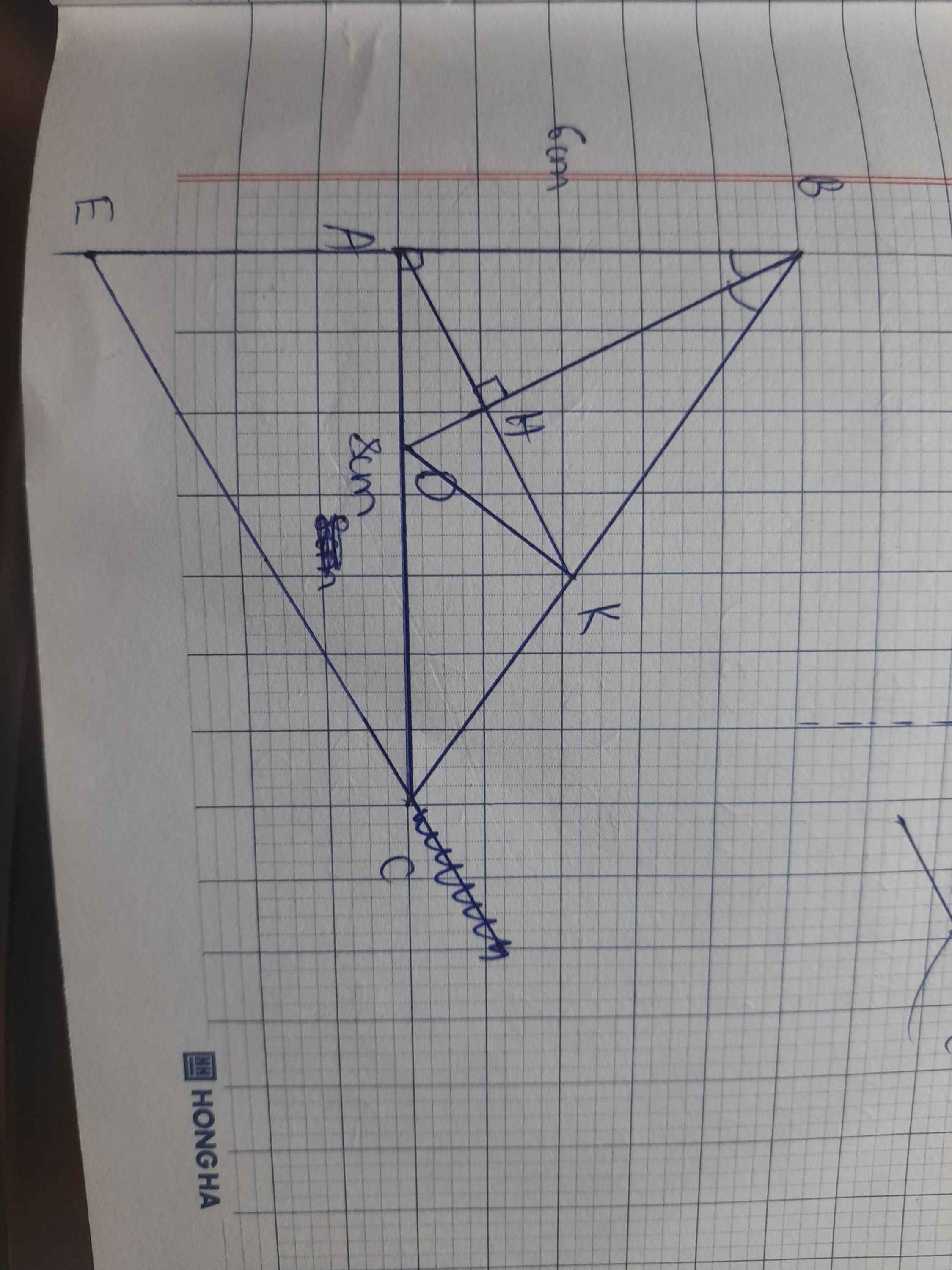
a) Xét tam giác vuông ABC
Theo định lý Py-ta-go ta có :
AB2 + AC2 = BC2
=> 62 + 82 = BC2
=> 36 + 64 = BC2
=> 100 = BC2
=> BC = 10cm
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A. AB 6cm, AC 8cm. Vẽ đường cao AH.
a) CMR: tam giác ABC đồng dạng tam giác HAC. AB×AC=BC×AH
b) Tính BC, BH
c) Vẽ HD vuông góc với AB tại D, HE vuông góc với AC tại E. Chứng minh AB×AD+AC×AE=2DE^2
Xem chi tiết