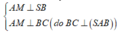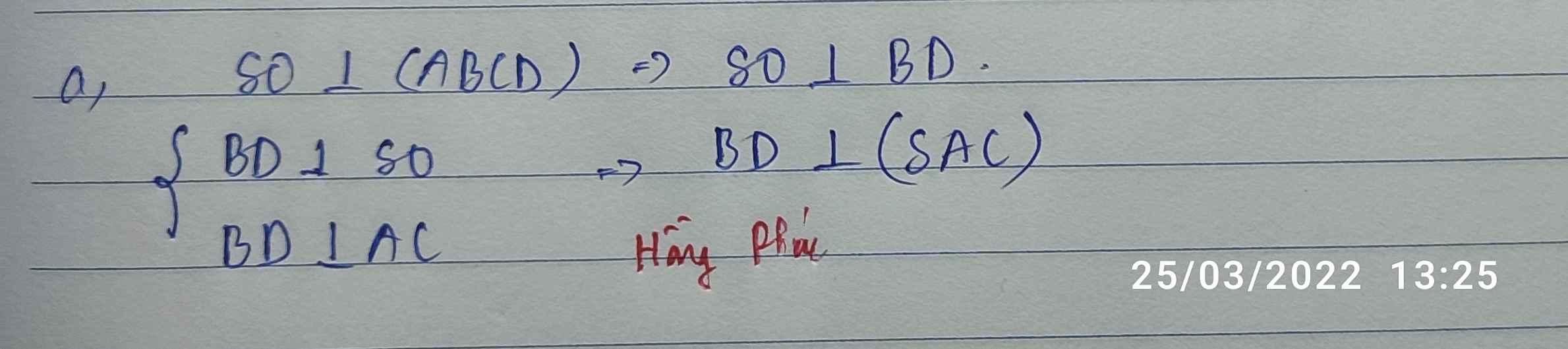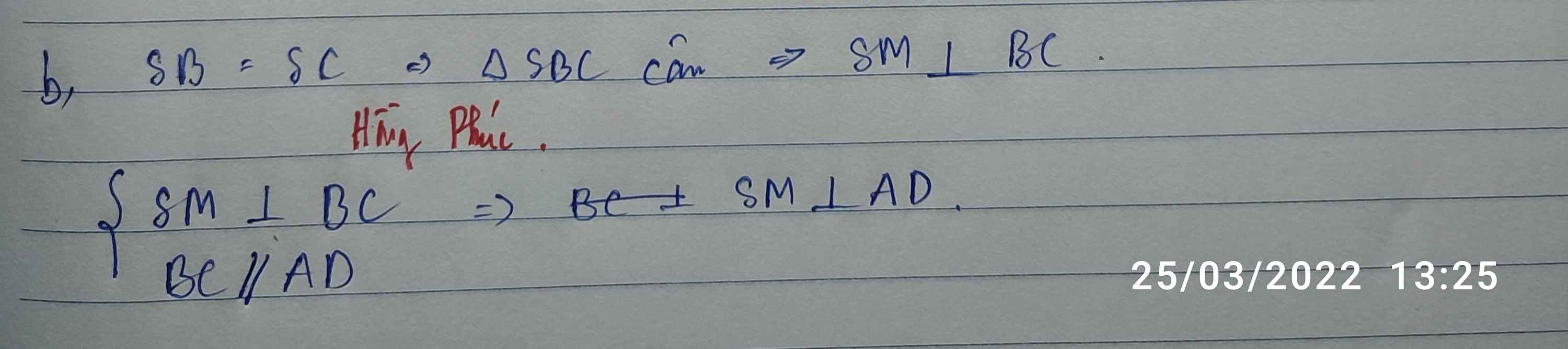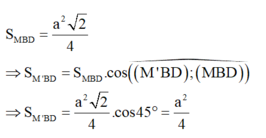Cho hình vuông ABCD. Gọi M; N là trung điểm của AB và BC. Các đường thẳng DN
và CM cắt nhau tại I. Chứng minh:
a/ DN vuông góc với CM
b/ ΔAID cân.

Những câu hỏi liên quan
cho hình vuông ABCD . gọi M là điiểm nằm trong hình vuông ABCD . CMR \(MA^2+MB^2+MC^2+MD^2\ge2\)
Bài 1 : cho hình chóp S.ABCD, ABCD là hình vuông cạnh a, SA= a căn 2 , SA vuông góc với ABCD. Gọi M,N lần lượg là hình chiếu của A lên SB,SD. CMR: SC vuông góc với (AMN )
+)CD⊥SA do SA vuông với ABCD
CD⊥AD( tính chất hình vuông)
=>CD⊥(SAD)=>CD⊥AN mà SD⊥AN=> AN⊥(SDC)=>AN⊥SC(1)
+) BC⊥SA do SA vuông với ABCD
BC⊥AB( tính chất hình vuông)
=>BC⊥(SAB)=>BC⊥AM mà SB⊥AM=> AM⊥(SAB)=>AM⊥SC(2)
TỪ 1 và 2 => SC⊥(AMN) đpcm
Đúng 0
Bình luận (0)
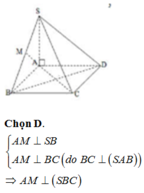
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, SA ⊥ (ABCD). Gọi M là hình chiếu của A trên SB. Khẳng định nào sau đây đúng?
A. AM ⊥ SD
B. AM ⊥ (SCD)
C. AM ⊥ CD
D. AM ⊥ (SBC)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông,
S
A
⊥
A
B
C
D
. Gọi M là hình chiếu của A trên SB. Khẳng định nào sau đây đúng? A.
A
M
⊥
S
D
B.
A...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, S A ⊥ A B C D . Gọi M là hình chiếu của A trên SB. Khẳng định nào sau đây đúng?
A. A M ⊥ S D
B. A M ⊥ S C D
C. A M ⊥ C D
D. A M ⊥ S B C
cho hình vuông ABCD , gọi M là trung điểm AB . Tính góc AMC
\(\widehat{AMC}\simeq117^0\)
Đúng 0
Bình luận (0)
Cho hình vuông ABCD. Gọi M,N là hai điểm lần lượt trên hai cạnh BC và CD sao cho góc MAN= 45 độ. Chứng minh chu vi tam giác CMN = 1/2 chu vi hình vuông ABCD
Trên tia đối của tia DC lấy E sao cho DE=BM
Xét ΔABM vuông tại B và ΔADE vuông tại D có
AB=AD
BM=DE
=>ΔABM=ΔADE
=>AM=AE
góc BAM+góc MAN+góc NAD=góc BAD=90 độ
=>góc BAM+góc NAD=45 độ
=>góc EAN=45 độ
Xét ΔEAN và ΔMAN có
AE=AM
góc EAN=góc MAN
AN chung
=>ΔEAN=ΔMAN
=>EN=MN
C CMN=CM+MN+CN
=CM+MN+CN
=CM+ED+DN+CN
=CM+BM+DN+CN
=BC+CD=1/2*C ABCD
Đúng 0
Bình luận (0)
cho hình chóp S.ABCD có đáy là hình vuông , gọi O là tâm của đáy SO vuông góc (ABCD)
a)Chứng minh BD vuông góc với (SAC)
b) gọi M là trung điểm của BC .Chứng minh SM vuông góc AD
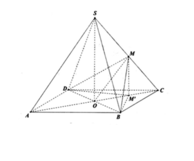
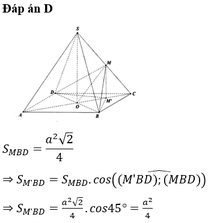
Cho hình chóp tứ giác đều S.ABCD có cạnh bên và cạnh đáy đều bằng a. Gọi O là tâm của ABCD. Gọi M là trung điểm SC và M là hình chiếu vuông góc của M lên (ABCD). Diện tích của tam giác M BD bằng: A.
a
2
6
8
B.
a
2
2
C. ...
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có cạnh bên và cạnh đáy đều bằng a. Gọi O là tâm của ABCD. Gọi M là trung điểm SC và M' là hình chiếu vuông góc của M lên (ABCD). Diện tích của tam giác M' BD bằng:
A. a 2 6 8
B. a 2 2
C. 2 a 2 8
D. a 2 4
Cho hình chóp tứ giác đều S.ABCD có cạnh bên và cạnh đáy đểu bằng a. Gọi O là tâm của ABCD. Gọi M là trung điểm SC và M là hình chiếu vuông góc của M lên (ABCD). Diện tích của tam giác M BD bằng A.
a
2
6
8
B.
a
2
2
C.
a...
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có cạnh bên và cạnh đáy đểu bằng a. Gọi O là tâm của ABCD. Gọi M là trung điểm SC và M' là hình chiếu vuông góc của M lên (ABCD). Diện tích của tam giác M' BD bằng
A. a 2 6 8
B. a 2 2
C. a 2 2 8
D. a 2 4
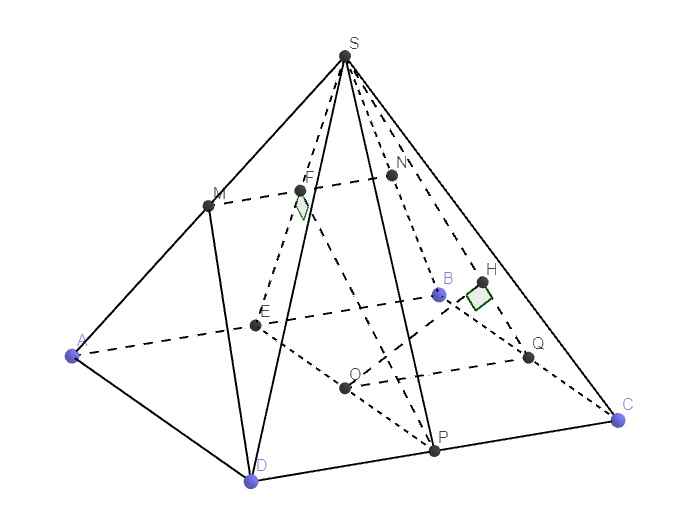
Cho hình chóp đều S ABCD, đáy ABCD là hình vuông cạnh 2a , tâm O . Gọi M là trung điểm SA.Tính d (OM;SB) Biết (MCD) ⊥ (SAB)
Dựng hình như hình vẽ (E, P, Q, N lần lượt là trung điểm các cạnh)
\(MN||AB\Rightarrow N\in\left(MCD\right)\)
F là giao điểm MN và SE \(\Rightarrow\) F cũng là trung điểm SE
Do tính đối xứng của chóp đều \(\Rightarrow MP=NP\Rightarrow PF\perp MN\) (trung tuyến đồng thời là đường cao)
\(\Rightarrow PF\perp\left(SAB\right)\) (do MN là giao tuyến của 2 mp vuông góc)
\(\Rightarrow PF\perp SE\Rightarrow\Delta SEP\) cân tại P (PF là trung tuyến kiêm đường cao)
\(\Rightarrow\Delta SEP\) đều (do chóp đều nên SEP cũng cân tại S)
\(\Rightarrow SO=a\sqrt{3}\)
MN song song và bằng 1/2 AB (đường trung bình)
OQ song song và bằng 1/2 AB (hiển nhiên)
\(\Rightarrow MNQO\) là hbh \(\Rightarrow OM||NQ\Rightarrow OM||\left(SBC\right)\)
\(\Rightarrow d\left(OM;SB\right)=d\left(OM;\left(SBC\right)\right)=d\left(O;\left(SBC\right)\right)\)
Từ O kẻ \(OH\perp SQ\Rightarrow OH=d\left(O;\left(SBC\right)\right)\)
\(\dfrac{1}{OH^2}=\dfrac{1}{OQ^2}+\dfrac{1}{SO^2}=\dfrac{1}{a^2}+\dfrac{1}{3a^2}\Rightarrow OH\)
Đúng 2
Bình luận (1)