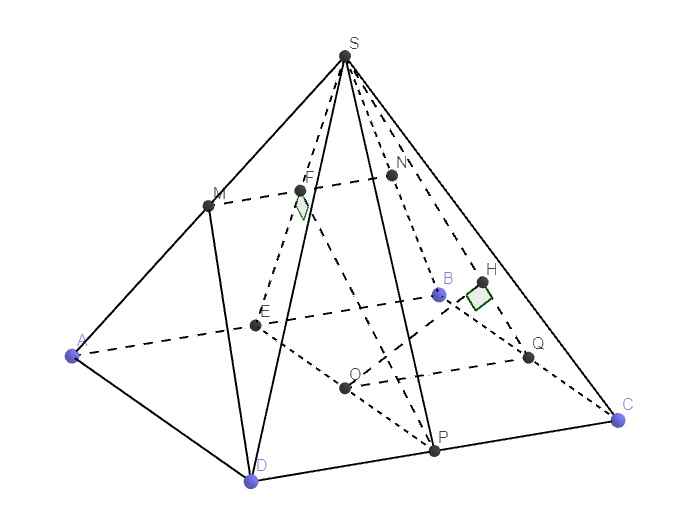
Dựng hình như hình vẽ (E, P, Q, N lần lượt là trung điểm các cạnh)
\(MN||AB\Rightarrow N\in\left(MCD\right)\)
F là giao điểm MN và SE \(\Rightarrow\) F cũng là trung điểm SE
Do tính đối xứng của chóp đều \(\Rightarrow MP=NP\Rightarrow PF\perp MN\) (trung tuyến đồng thời là đường cao)
\(\Rightarrow PF\perp\left(SAB\right)\) (do MN là giao tuyến của 2 mp vuông góc)
\(\Rightarrow PF\perp SE\Rightarrow\Delta SEP\) cân tại P (PF là trung tuyến kiêm đường cao)
\(\Rightarrow\Delta SEP\) đều (do chóp đều nên SEP cũng cân tại S)
\(\Rightarrow SO=a\sqrt{3}\)
MN song song và bằng 1/2 AB (đường trung bình)
OQ song song và bằng 1/2 AB (hiển nhiên)
\(\Rightarrow MNQO\) là hbh \(\Rightarrow OM||NQ\Rightarrow OM||\left(SBC\right)\)
\(\Rightarrow d\left(OM;SB\right)=d\left(OM;\left(SBC\right)\right)=d\left(O;\left(SBC\right)\right)\)
Từ O kẻ \(OH\perp SQ\Rightarrow OH=d\left(O;\left(SBC\right)\right)\)
\(\dfrac{1}{OH^2}=\dfrac{1}{OQ^2}+\dfrac{1}{SO^2}=\dfrac{1}{a^2}+\dfrac{1}{3a^2}\Rightarrow OH\)
cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh 2a, góc BAD=120. Mặt bên (SAB) có SA=a, SB= a\(\sqrt{3}\) và vuông góc với mặt phẳng đáy. Gọi G là trọng tâm tam giác SCD. Tính thể tích hình chóp SABCD và khoảng cách từ G đến mặt phẳng (SAB). 
