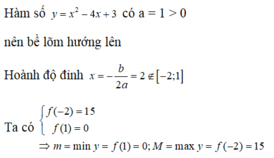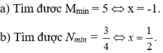tìm giá trị nhỏ nhất của m=x(x+1)(x2+x-4)

Những câu hỏi liên quan
Tìm giá trị của m để phương trình
x
2
+ (4m + 1)x + 2(m – 4) 0 có hai nghiệm
x
1
;
x
2
và biểu thức
A
(
x
1
−
x
2
)
2
đạt giá trị nhỏ nhất A. m 1 B. m 0...
Đọc tiếp
Tìm giá trị của m để phương trình x 2 + (4m + 1)x + 2(m – 4) = 0 có hai nghiệm x 1 ; x 2 và biểu thức A = ( x 1 − x 2 ) 2 đạt giá trị nhỏ nhất
A. m = 1
B. m = 0
C. m = 2
D. m = 3
Phương trình x 2 + (4m + 1)x + 2(m – 4) = 0 có a = 1 ≠ 0 và
∆ = ( 4 m + 1 ) 2 – 8 ( m – 4 ) = 16 m 2 + 33 > 0 ; ∀ m
Nên phương trình luôn có hai nghiệm x 1 ; x 2
Theo hệ thức Vi-ét ta có x 1 + x 2 = − 4 m − 1 x 1 . x 2 = 2 n − 8
Xét
A = x 1 - x 2 2 = x 1 + x 2 2 - 4 x 1 x 2 = 16 m 2 + 33 ≥ 33
Dấu “=” xảy ra khi m = 0
Vậy m = 0 là giá trị cần tìm
Đáp án: B
Đúng 0
Bình luận (0)
Cho các số thực dương x, y thỏa mãn
x
2
+
x
x
+
1
y
+
2
x
+
1
y
+
1
. Gọi M, m lần lượt là giá trị lớn nhất, giá t...
Đọc tiếp
Cho các số thực dương x, y thỏa mãn x 2 + x x + 1 = y + 2 x + 1 y + 1 . Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức P = - x 2 + x + 4 + 4 - x 2 - x + 1 y + 1 + a . Có bao nhiêu giá trị nguyên của tham số a ∈ - 10 ; 10 để M ≤ 2 m
A. 4
B. 5
C. 6
D. 7
Chọn đáp án B
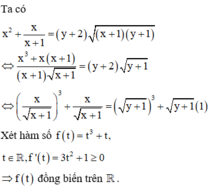
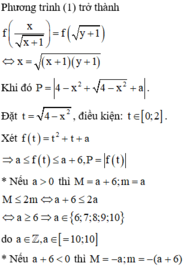
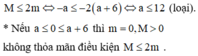
Vậy có 5 giá trị nguyên của m thỏa mãn điều kiện.
Đúng 0
Bình luận (0)
Bài 1: Tìm giá trị nhỏ nhất của biểu thức
a, M= x2-10x+3
b, N= x2-x+2
c, P=3x2-12x
Bài 2: Tìm giá trị nhỏ nhất của biểu thức
a, M= 2x2-4x+3
b, N= x2-4x+5+y2+2y2
MONG MN GIÚP ĐỠ :3
Bài 1:
a: \(M=x^2-10x+3\)
\(=x^2-10x+25-22\)
\(=\left(x^2-10x+25\right)-22\)
\(=\left(x-5\right)^2-22>=-22\forall x\)
Dấu '=' xảy ra khi x-5=0
=>x=5
b: \(N=x^2-x+2\)
\(=x^2-x+\dfrac{1}{4}+\dfrac{7}{4}\)
\(=\left(x-\dfrac{1}{2}\right)^2+\dfrac{7}{4}>=\dfrac{7}{4}\forall x\)
Dấu '=' xảy ra khi x-1/2=0
=>x=1/2
c: \(P=3x^2-12x\)
\(=3\left(x^2-4x\right)\)
\(=3\left(x^2-4x+4-4\right)\)
\(=3\left(x-2\right)^2-12>=-12\forall x\)
Dấu '=' xảy ra khi x-2=0
=>x=2
Đúng 2
Bình luận (0)
Cho x2+y2=6 .
a)Tìm giá trị nhỏ nhất của A=x 4+y4
b) Tìm giá trị lớn nhất của B=x+y; C=xy
Lời giải:
a. Áp dụng BĐT Cô-si:
$x^4+9\geq 6x^2$
$y^4+9\geq 6y^2$
$\Rightarrow x^4+y^4+18\geq 6(x^2+y^2)$
$A+18\geq 36$
$A\geq 18$
Vậy GTNN của $A$ là $18$ khi $x^2=y^2=3$
b.
$(x-y)^2\geq 0$
$\Leftrightarrow x^2+y^2\geq 2xy$
$\Leftrightarrow 2(x^2+y^2)\geq (x+y)^2$
$\Leftrightarrow 12\geq (x+y)^2$
$\Rightarrow B=x+y\leq \sqrt{12}$. Vậy $B$ max bằng $\sqrt{12}$ khi $x=y=\sqrt{3}$
$(x-y)^2\geq 0$
$\Leftrightarrow x^2+y^2\geq 2xy$
$\Leftrightarrow 6\geq 2C$
$\Leftrightarrow C\leq 3$. Vậy $C_{\max}=3$. Giá trị này đạt tại $x=y=-\sqrt{3}$
Đúng 0
Bình luận (0)
Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số y = f(x) = x 2 − 4x + 3 trên đoạn [−2; 1].
A. M = 15; m = 1.
B. M = 15; m = 0.
C. M = 1; m = −2.
D. M = 0; m = −15.
1) cho pT: x² = mx + m−3 = 0 Tìm giá trị nhỏ nhất của P= 2(x² + x2²)-X6X2.
với giá trị nào của x thì biểu thức M=x2+2x-(2+x)(4-2x+x2)+x3 đạt giá trị nhỏ nhất
\(M=x^2+2x-8-x^3+x^3=x^2+2x-8=\left(x^2+2x+1\right)-9=\left(x+1\right)^2-9\ge-9\)
\(minM=-9\Leftrightarrow x=-1\)
Đúng 1
Bình luận (0)
\(M=x^2+2x-8-x^3+x^3=\left(x^2+2x+1\right)-9=\left(x+1\right)^2-9\ge-9\\ M_{min}=-9\Leftrightarrow x=-1\)
Đúng 1
Bình luận (0)
cho phương trình x^2-(m+1)x+m-8 =0 tìm giá trị nhỏ nhất của x1^2+(m+1)x2-3m+2
Áp dụng Viét có: `{(x_1+x_2=-b/a=m+1),(x_1.x_2=c/a=m-8):}`
Ta có: `x_1 ^2+(m+1)x_2 -3m+2`
`=x_1 ^2+(x_1+x_2)x_2 -3m+2`
`=(x_1+x_2)^2-x_1.x_2-3m+2`
`=(m+1)^2-(m-8)-3m+2`
`=m^2+2m+1-m+8-3m+2`
`=m^2-2m+1+10`
`=(m-1)^2+10 >= 10`
`=>Mi n=10`
Dấu "`=`" xảy ra `<=>m-1=0<=>m=1`
Đúng 1
Bình luận (0)
Tìm giá trị nhỏ nhất của biểu thức:
a) M = 2 x 2 +4x + 7; b)N = x 2 -x +1.
Cho pt : x^2-(m+1)x+m=0.
Gọi x1, x2 là hai nghiệm của pt. Tìm giá trị m để A=x1^2x2+x1x2^2+2007 đạt giá trị nhỏ nhất. Tìm giá trị nhỏ nhất đó.
Mọi người giúp giùm... cảm ơn ạk