Tìm giới hạn :
Những câu hỏi liên quan
Cho dãy số
(
u
n
)
xácđịnh bởi công thức truy hồi
u
1
2
u
n
+...
Đọc tiếp
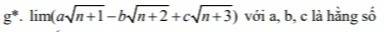
Cho dãy số ( u n ) xácđịnh bởi công thức truy hồi u 1 = 2 u n + 1 = u n + 1 2 v ớ i n ≥ 1
Chứng minh rằng có giới hạn hữu hạn khi Tìm giới hạn đó.
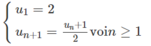
Ta có
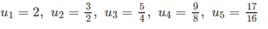
Dự đoán
Chứng minh dự đoán trên bằng quy nạp (bạn đọc tự chứng minh).
Từ đó
Đúng 0
Bình luận (0)
Tìm các giới hạn sau: Giới hạn
lim
1
-
2
.
3
n
-
2
2
n
-
12
.
3
n
-
1
bằng
a...
Đọc tiếp
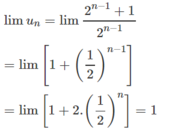
Tìm các giới hạn sau: Giới hạn lim 1 - 2 . 3 n - 2 2 n - 12 . 3 n - 1
bằng a b (phân số tối giản). Giá trị A = b - 17 a - a b là:
A. 1 9
B. 1 18
C. - 1 9
D. 17 18
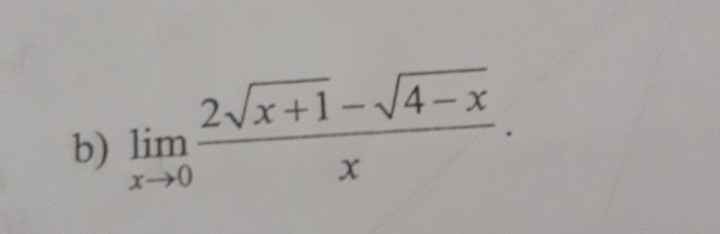
Tìm giới hạn
\(\lim\limits_{x\rightarrow0}\dfrac{2\sqrt{x+1}-\sqrt{4-x}}{x}=\lim\limits_{x\rightarrow0}\dfrac{4\left(x+1\right)-\left(4-x\right)}{x\left(2\sqrt{x+1}+\sqrt{4-x}\right)}\)
\(=\lim\limits_{x\rightarrow0}\dfrac{5x}{x\left(2\sqrt{x+1}+\sqrt{4-x}\right)}=\lim\limits_{x\rightarrow0}\dfrac{5}{2\sqrt{x+1}+\sqrt{4-x}}=\dfrac{5}{4}\)
Đúng 0
Bình luận (0)
Cho dãy số
(
u
n
)
xác định bởi
u
1
1
u
n
+
1...
Đọc tiếp
Cho dãy số ( u n ) xác định bởi u 1 = 1 u n + 1 = 2 u n + 3 u n + 2 v ớ i n ≥ 1
a) Chứng minh rằng u n > 0 với mọi n.
b) Biết ( u n ) có giới hạn hữu hạn. Tìm giới hạn đó.
Tìm giới hạn sau:
Ta có : \(A=lim_{x\rightarrow1}\dfrac{\sqrt{2x-1}-x}{x^2-1}=lim_{x\rightarrow1}\dfrac{2x-1-x^2}{\left(x^2-1\right)\left(\sqrt{2x-1}+x\right)}\) \(=lim_{x\rightarrow1}\dfrac{-\left(x-1\right)^2}{\left(x-1\right)\left(x+1\right)\left(\sqrt{2x-1}+x\right)}\) \(=lim_{x\rightarrow1}\dfrac{1-x}{\left(x+1\right)\left(\sqrt{2x-1}+x\right)}=0\)
Đúng 1
Bình luận (0)
Cho \(\left\{{}\begin{matrix}u_1=2021\\u_{n+1}=\dfrac{1}{2}\left(u_n+\dfrac{2020}{u_n}\right)\end{matrix}\right.\) CMR un có giới hạn và tìm giới hạn đó
Dễ dàng nhận ra (hoặc chứng minh bằng quy nạp) dãy đã cho là dãy dương
\(u_{n+1}=\dfrac{1}{2}\left(u_n+\dfrac{2020}{u_n}\right)\ge\dfrac{1}{2}.2\sqrt{2020}=\sqrt{2020}\)
\(\Rightarrow\) Dãy bị chặn dưới bởi \(\sqrt{2020}\)
Mặt khác:
\(\dfrac{u_{n+1}}{u_n}=\dfrac{1}{2}\left(1+\dfrac{2020}{u_n^2}\right)\le\dfrac{1}{2}\left(1+\dfrac{2020}{\sqrt{2020}^2}\right)=1\)
\(\Rightarrow u_{n+1}\le u_n\Rightarrow\) dãy giảm
Dãy giảm và bị chặn dưới \(\Rightarrow\) dãy có giới hạn
Gọi giới hạn đó là L \(\Rightarrow\sqrt{2020}\le L\le2021\)
Lấy giới hạn 2 vế của \(u_{n+1}=\dfrac{1}{2}\left(u_n+\dfrac{2020}{u_n}\right)\Rightarrow L=\dfrac{1}{2}\left(L+\dfrac{2020}{L}\right)\)
\(\Rightarrow L^2=2020\Rightarrow L=\sqrt{2020}\)
Đúng 0
Bình luận (2)
Cho dãy un xác định bởi \(u_1=1\)và \(\dfrac{u_{n-1}^2+2021}{2u_{n-1}}\).Chứng minh dãy đó có giới hạn và tìm giới hạn dãy đó
Dễ thấy \(u_n>0,\forall n\inℕ^∗\).
Ta có \(u_{n+1}-u_n=\dfrac{u_n^2+2021}{2u_n}-u_n=\dfrac{2021-u_n^2}{2u_n}\)
Với \(n\ge2\) thì \(u_n=\dfrac{u_{n-1}^2+2021}{2u_{n-1}}\) \(=\dfrac{u_{n-1}}{2}+\dfrac{2021}{2u_{n-1}}\) \(>2\sqrt{\dfrac{u_{n-1}}{2}.\dfrac{2021}{2u_{n-1}}}\) \(=\sqrt{2021}\)
Vậy \(u_n>\sqrt{2021},\forall n\ge2\), suy ra \(u_{n+1}-u_n=\dfrac{2021-u_n^2}{2u_n}< 0,\forall n\inℕ^∗\)
\(\Rightarrow\) Dãy \(\left(u_n\right)\) là dãy giảm. Mà \(u_n>\sqrt{2021}\) \(\Rightarrow\left(u_n\right)\) có giới hạn hữu hạn. Đặt \(\lim\limits_{n\rightarrow+\infty}u_n=L\) \(\Rightarrow L=\dfrac{L^2+2021}{2L}\) \(\Leftrightarrow L=\sqrt{2021}\)
Vậy \(\lim\limits_{n\rightarrow+\infty}u_n=\sqrt{2021}\)
Đúng 0
Bình luận (0)
Dễ thấy .
Ta có
Với thì
Vậy , suy ra
Dãy là dãy giảm. Mà có giới hạn hữu hạn. Đặt
Vậy
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Tìm các giá trị của m để giới hạn
lim
x
→
+
∞
(
m
x
2
+
2
x
-
x
+
2018
)
là hữu hạn A. m 1 B. m 0 C. m
∈
{
-
1
;
1
}
D. m ...
Đọc tiếp
Tìm các giá trị của m để giới hạn lim x → + ∞ ( m x 2 + 2 x - x + 2018 ) là hữu hạn
A. m = 1
B. m > 0
C. m ∈ { - 1 ; 1 }
D. m ∈ { - 2 ; 2 }
Tìm các giá trị của m để giới hạn
lim
x
→
+
∞
m
x
2
+
2
x
-
x
+
2018
là hữu hạn. A. m 1 B. m 0 C.
m
∈...
Đọc tiếp
Tìm các giá trị của m để giới hạn lim x → + ∞ m x 2 + 2 x - x + 2018 là hữu hạn.
A. m = 1
B. m > 0
C. m ∈ - 1 ; 1
D. m ∈ - 2 ; 2
