Cho đa giác đều 30 đỉnh. Chứng minh rằng trong các đỉnh đó , bất kì một bộ gồm 9 đỉnh nào đều chứa 4 đỉnh tạo lên một hình thang cân.

Những câu hỏi liên quan
cho đa giác đều 30 đỉnh chứng minh rằng trong các đỉnh đó bất kì bộ gồm 9 đỉnh nào đều chứa 4 đỉnh tạo nên hình thang cân
Cho đa giác đều gồm 2017 cạnh. Người ta sơn các đỉnh của đa giác bằng 2 màu xanh và đỏ. Chứng minh tồn tại 3 đỉnh được sơn cùng một màu tạo thành một tam giác cân.
cho đa giác đều gồm 1999 cạnh. Người ta sơn các đỉnh của đa giác bằng hai màu xanh và đỏ. Chứng minh ràng tồn tại ba đỉnh được sơn cùng một màu tạo thành một đa giác cân
Ta có đa giác 1999 cạnh nên có 1999 đỉnh. Do đó phải tồn tại 2 đỉnh kề nhau là P và Q đc sơn bởi cùng 1 màu- màu đỏ (Theo nguyên tắc dirichlet)
Vì đa giác đã cho là đa giác đều có số đỉnh lẻ nên phải tồn tại 1 đỉnh nào đó nằm trên đường trung trực của đoạn thẳng PQ. Giả sử đỉnh đó là A
-Nếu A tô màu đỏ thì ta có tam giác APQ là tam giác cân có 3 đỉnh A, P, Q đc tô cùng màu đỏ
-Nếu A tô màu xanh. Lúc đó gọi B và C là các đỉnh khác nhau của đa giác kề vs P và Q
-Nếu cả 2 đỉnh B và C đc tô màu xanh thì tam giác ABC cân và có 3 đỉnh cùng tô màu xanh
-Nếu ngược lại, 1 trong 2 đỉnh B và C đc tô màu đỏ thì tam giác BPQ hoặc tam giác CPQ là tam giác cân có 3 đỉnh đc tô màu đỏ
NGUYÊN LÍ DIRICHLE Bạn đã học chưa P/s hình như nó lớp 9 mà : )
Đúng 0
Bình luận (0)
mình chưa học nhưng để mình tìm hiểu xem sao với lại sao bạn không trả lời mình vậy
Đúng 0
Bình luận (0)
ĐỀ THI GIAO LƯU HSG LỚP 8 CẤP HUYỆN
NĂM HỌC 2014-2015
Cho đa giác đều gồm 1999 cạnh. Người ta sơn các đỉnh của đa giác bằng hai màu xanh
và đỏ. Chứng minh rằng tồn tại ba đỉnh được sơn cùng một màu tạo thành một tam giác cân
Ta có đa giác 1999 cạnh nên có 1999 đỉnh. Do đó phải tồn tại 2 đỉnh kề nhau là P và Q đc sơn bởi cùng 1 màu- màu đỏ (Theo nguyên tắc dirichlet)
Vì đa giác đã cho là đa giác đều có số đỉnh lẻ nên phải tồn tại 1 đỉnh nào đó nằm trên đường trung trực của đoạn thẳng PQ. Giả sử đỉnh đó là A
-Nếu A tô màu đỏ thì ta có tam giác APQ là tam giác cân có 3 đỉnh A, P, Q đc tô cùng màu đỏ
-Nếu A tô màu xanh. Lúc đó gọi B và C là các đỉnh khác nhau của đa giác kề vs P và Q
-Nếu cả 2 đỉnh B và C đc tô màu xanh thì tam giác ABC cân và có 3 đỉnh cùng tô màu xanh
-Nếu ngược lại, 1 trong 2 đỉnh B và C đc tô màu đỏ thì tam giác BPQ hoặc tam giác CPQ là tam giác cân có 3 đỉnh đc tô màu đỏ
Đúng 8
Bình luận (2)
Cho đa giác đều gồm 1999 cạnh . Người ta sơn các đỉnh của đa giác bằng 2 màu xanh và đỏ . chứng minh rằng tồm tại 3 đỉnh được sơn cùng 1 màu tạo thành 1 tam giác cân
Có thể xếp hay không các số 0, 1, 2, ...,9 lên các đỉnh của một đa giác đều 10 đỉnh sao cho hiệu số trên 2 đỉnh kề nhau bất kỳ nhận một trong các giá trị -3, -4, -5, 3, 4 hoặc 5 .
MẤY BẠN GIÚP MÌNH VS.
Cho một tam giác đều 15 cạnh. Chứng minh rằng khi chọn ra 7 điểm bất kỳ trong số 15 điểm trên thì luôn có 3 đỉnh là đỉnh của 1 tam giác cân.
Sửa đề: Đa giác đều 15 cạnh
=>Tạo ra 3 ngũ giác đều trong đó: Ngũ giác 1 có các đỉnh tô màu đỏ, ngũ giác 2 có các đỉnh tô màu xanh, ngũ giác 3 có các đỉnh tô màu vàng. Ta sẽ xem 3 ngũ giác đó như là 3 khu, 7 điểm ta chọn ra 7 điểm trong đó.
=>7 điểm thuộc vào 3 khu khác nhau thì phải có 1 khu có 3 điểm.
=>Luôn có tam giác cân(3 đỉnh bất kì của một ngũ giác đều tạo thành tam giác cân)
Đúng 1
Bình luận (0)
Cho một đa giác đều 2n đỉnh Tìm n biết số hình chữ nhật được tạo ra từ bốn đỉnh trong số 2n đỉnh của đa giác đó là 45 A. n 12 B. n 10 C. n 9 D. n 45
Đọc tiếp
Cho một đa giác đều 2n đỉnh 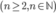 Tìm n biết số hình chữ nhật được tạo ra từ bốn đỉnh trong số 2n đỉnh của đa giác đó là 45
Tìm n biết số hình chữ nhật được tạo ra từ bốn đỉnh trong số 2n đỉnh của đa giác đó là 45
A. n = 12
B. n = 10
C. n = 9
D. n = 45
Đáp án B
Đa giác đều 2n đỉnh có n đường chéo qua tâm. Cứ 2 đường chéo qua tâm tương ứng với 1 hình chữ nhật 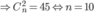
![]()
Đúng 0
Bình luận (0)
tại mỗi đỉnh của 1 đa giác đều 11 cạnh ta ghi 1 số bất kì trong các số:31,32,61,62,91,92,331,332,361,362,961(mỗi số dùng 1 lần).c/m luôn tồn tại 3 đỉnh của đa giác là 3 đỉnh của 1 tam giác cân và tổng các số ghi trên đỉnh tam giác đó là số chia hết 3


















