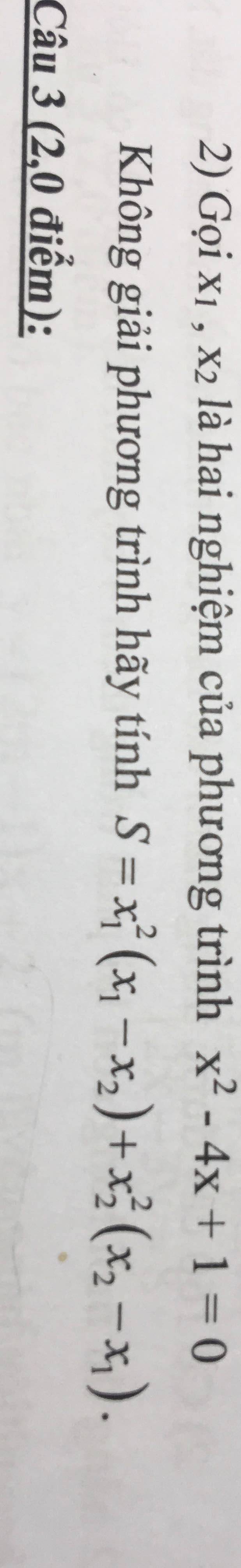Giải giúp mình câu này với ạ

Những câu hỏi liên quan
Giải giúp mình bài này với ạ giải câu c chi tiết xíu giúp mình với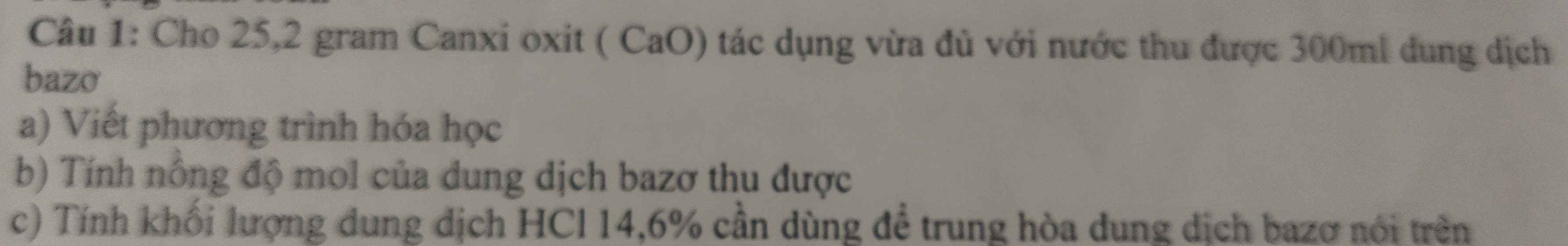
Giúp mình câu này với ạ, đc thì giải chi tiết giúp mình luôn ạ, đbt là câu b, mình hơi chậm hiểu 
Nãy ghi nhầm =="
a)Hđ gđ là nghiệm pt
`x^2=2x+2m+1`
`<=>x^2-2x-2m-1=0`
Thay `m=1` vào pt ta có:
`x^2-2x-2-1=0`
`<=>x^2-2x-3=0`
`a-b+c=0`
`=>x_1=-1,x_2=3`
`=>y_1=1,y_2=9`
`=>(-1,1),(3,9)`
Vậy tọa độ gđ (d) và (P) là `(-1,1)` và `(3,9)`
b)
Hđ gđ là nghiệm pt
`x^2=2x+2m+1`
`<=>x^2-2x-2m-1=0`
PT có 2 nghiệm pb
`<=>Delta'>0`
`<=>1+2m+1>0`
`<=>2m> -2`
`<=>m> 01`
Áp dụng hệ thức vi-ét:`x_1+x_2=2,x_1.x_2=-2m-1`
Theo `(P):y=x^2=>y_1=x_1^2,y_2=x_2^2`
`=>x_1^2+x_2^2=14`
`<=>(x_1+x_2)^2-2x_1.x_2=14`
`<=>4-2(-2m-1)=14`
`<=>4+2(2m+1)=14`
`<=>2(2m+1)=10`
`<=>2m+1=5`
`<=>2m=4`
`<=>m=2(tm)`
Vậy `m=2` thì ....
Đúng 1
Bình luận (0)
mọi người ơi giúp mình câu này với ạ, lời giải chi tiết càng tốt ạ, mình khá rối với câu này -.- cảm ơn mọi người nhiều
\(y'=\dfrac{\left(-2x+2\right)\left(x-3\right)-\left(-x^2+2x+c\right)}{\left(x-3\right)^2}=\dfrac{-x^2+6x-6-c}{\left(x-3\right)^2}\)
\(\Rightarrow\) Cực đại và cực tiểu của hàm là nghiệm của: \(-x^2+6x-6-c=0\) (1)
\(\Delta'=9-\left(6+c\right)>0\Rightarrow c< 3\)
Gọi \(x_1;x_2\) là 2 nghiệm của (1) \(\Rightarrow\left\{{}\begin{matrix}-x_1^2+6x_1-6=c\\-x_2^2+6x_2-6=c\end{matrix}\right.\)
\(\Rightarrow m-M=\dfrac{-x_1^2+2x_1+c}{x_1-3}-\dfrac{-x_2^2+2x_2+c}{x_2-3}=4\)
\(\Leftrightarrow\dfrac{-2x_1^2+8x_1-6}{x_1-3}-\dfrac{-2x_2^2+8x_2-6}{x_2-3}=4\)
\(\Leftrightarrow2\left(1-x_1\right)-2\left(1-x_2\right)=4\)
\(\Leftrightarrow x_2-x_1=2\)
Kết hợp với Viet: \(\left\{{}\begin{matrix}x_2-x_1=2\\x_1+x_2=6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_1=2\\x_2=4\end{matrix}\right.\)
\(\Rightarrow c=2\)
Có 1 giá trị nguyên
Đúng 0
Bình luận (0)
giúp mình cái này với ạ!:< ở câu b ý ạ câu a em giải rồi ạ!
Giải giúp mình câu 4 này với ạ gấp lắm ạ 
a) \(d\left(A;\Delta\right)=\dfrac{\left|4.1-3.3+2\right|}{\sqrt{4^2+\left(-3\right)^2}}=\dfrac{3}{5}\)
b) \(\overrightarrow{AB}=\left(-3;-2\right)\) là VTCP của đường thẳng d
PT tham số của d: \(\left\{{}\begin{matrix}x=1-3t\\y=3-2t\end{matrix}\right.\left(t\in R\right)\)
c) Đường tròn (C) có bán kính \(R=AB=\sqrt{\left(1+2\right)^2+\left(3-1\right)^2}=\sqrt{13}\)
PT đường tròn (C): \(\left(x-1\right)^2+\left(y-3\right)^2=13\)
Đúng 3
Bình luận (0)
Giải giúp mình câu này với ạ

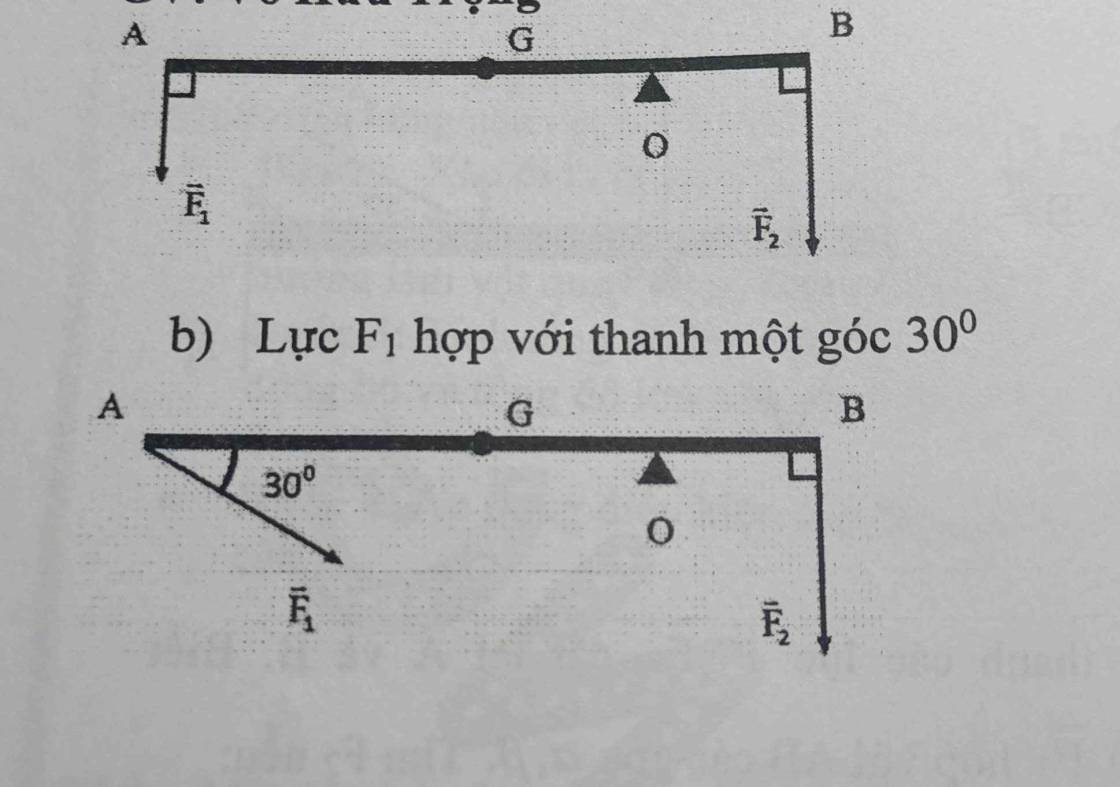
giúp mình giải câu này với ạ
a) AD đk cân bằng momen ta có
`F_1 *OA + P*GO = OB*F_2`
`<=> F_1 *(AB-OB) + mg(AB-OB - AB/2) = OB *F_2`
`<=> F_1 (120 - 30) + 2*10*(120 - 30 -120/2) = 30*50`
`=> F_1 = 10N`
b) AD đk cân bằng momen ta có
`F_1 * sin30^o *OA + P*GO = OB*F_2`
`<=> F_1 *sin30^o *(AB-OB) + mg(AB-OB - AB/2) = OB *F_2`
`<=> F_1*sin30^o * (120 - 30) + 2*10*(120 - 30 -120/2) = 30*50`
`=> F_1 = 20(N)`
Đúng 1
Bình luận (0)
giải giúp mình câu này với ạ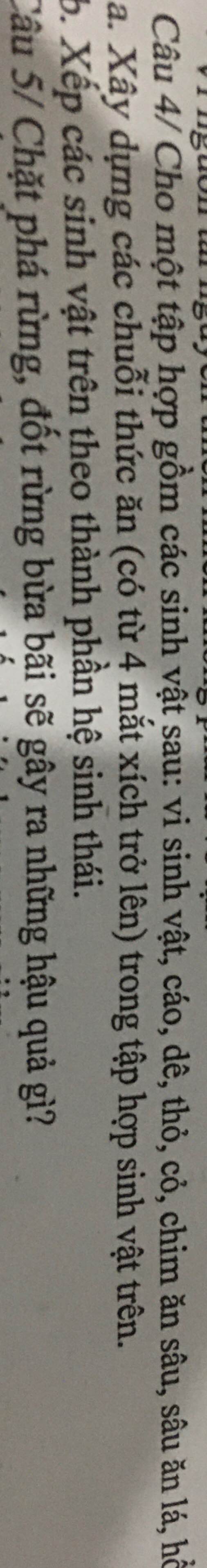
Giải giúp mình câu này với ạ
\(x^2-4x+1=0\)
\(\text{Δ}=\left(-4\right)^2-4\cdot1\cdot1=16-4=12>0\)
=>Phương trình có hai nghiệm phân biệt
\(x_1+x_2=-\left(-4\right)=4;x_1\cdot x_2=1\)
\(S=x_1^2\left(x_1-x_2\right)+x_2^2\left(x_2-x_1\right)\)
\(=x_1^2\left(x_1-x_2\right)-x_2^2\left(x_1-x_2\right)\)
\(=\left(x_1-x_2\right)\left(x_1^2-x_2^2\right)\)
\(=\left(x_1+x_2\right)\left(x_1-x_2\right)^2\)
\(=\left(x_1+x_2\right)\left[\left(x_1+x_2\right)^2-4x_1x_2\right]\)
\(=4\cdot\left[4^2-4\cdot1\right]\)
\(=4\cdot\left(16-4\right)=4\cdot12=48\)
Đúng 1
Bình luận (0)