\(x^2-4x+1=0\)
\(\text{Δ}=\left(-4\right)^2-4\cdot1\cdot1=16-4=12>0\)
=>Phương trình có hai nghiệm phân biệt
\(x_1+x_2=-\left(-4\right)=4;x_1\cdot x_2=1\)
\(S=x_1^2\left(x_1-x_2\right)+x_2^2\left(x_2-x_1\right)\)
\(=x_1^2\left(x_1-x_2\right)-x_2^2\left(x_1-x_2\right)\)
\(=\left(x_1-x_2\right)\left(x_1^2-x_2^2\right)\)
\(=\left(x_1+x_2\right)\left(x_1-x_2\right)^2\)
\(=\left(x_1+x_2\right)\left[\left(x_1+x_2\right)^2-4x_1x_2\right]\)
\(=4\cdot\left[4^2-4\cdot1\right]\)
\(=4\cdot\left(16-4\right)=4\cdot12=48\)




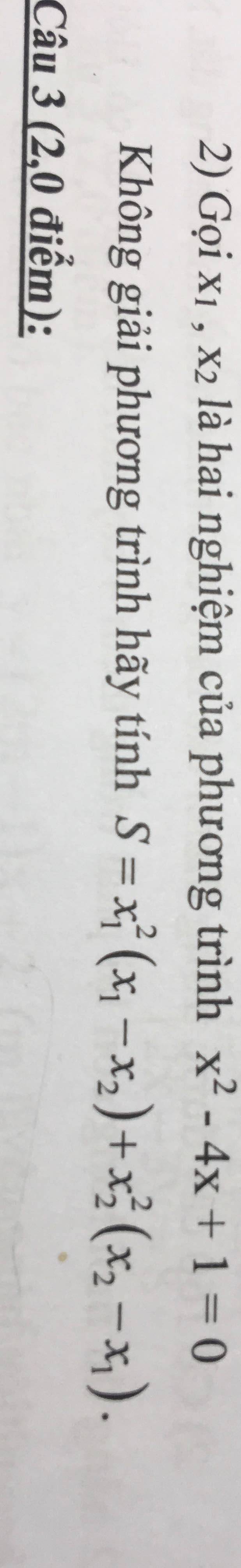

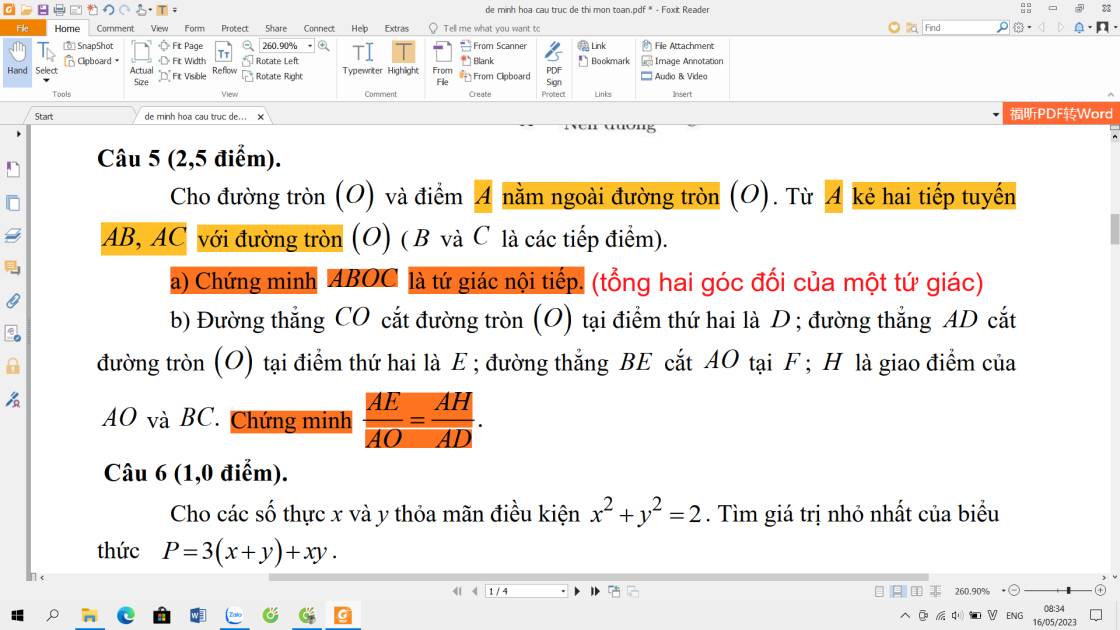 giải giúp mình 2 câu này với ạ
giải giúp mình 2 câu này với ạ










 ai giúp mình giải câu này với ạ, mình cám ơn mn nhiều
ai giúp mình giải câu này với ạ, mình cám ơn mn nhiều
