Cho tam giác ABC có a-b=2,hc=2,A=30o
a)Tính cosB
b)Tính diện tích tam giác ABC
Cho tam giác ABC có BC = 2 cm, góc A=105o , góc C=30o. Tính diện tích tam giác ABC.
Ta có :
góc C = 180o - 105o - 30o = 45o
Kẻ đường cao AH
Gọi BH = x(cm) $\to$ CH = 2 - x(cm)
Trong tam giác AHB vuông tại H và tam giác AHC vuông tại H, ta có :
\(AH=BH.tanB=x.tan45^o=x\\ AH=CH.tanC=\left(2-x\right).tan30^o=\dfrac{\sqrt{3}}{3}\left(2-x\right)\)
Suy ra :
\(x=\dfrac{\sqrt{3}}{3}\left(2-x\right)\Leftrightarrow x=\dfrac{2\sqrt{3}}{3+\sqrt{3}}\)
Suy ra:
\(S_{ABC}=\dfrac{1}{2}AH.BC=\dfrac{1}{2}.\dfrac{2\sqrt{3}}{3+\sqrt{3}}.2\simeq0,732\left(cm^2\right)\)
Tam giác ABC có cạnh a=2√3, b=2, và C=30o . Tính cạnh c, góc A và diện tích tam giác đó
mn giúp ạ
Lời giải:
Theo định lý cos:
\(\cos C=\frac{a^2+b^2-c^2}{2ab}\Leftrightarrow \cos 30^0=\frac{12+4-c^2}{8\sqrt{3}}\)
\(\Rightarrow c^2=4\Rightarrow c=2\)
$c=b=2$ nên tam giác $ABC$ cân tại $A$
$\Rightarrow \widehat{A}=180^0-2.30^0=120^0$
$S_{ABC}=\frac{1}{2}ab\sin C=\frac{1}{2}.2.2\sqrt{3}\sin 30^0=\sqrt{3}$ (đvdt)
Bài 4: Cho tam giác ABC vuông tại A có góc B= 30o, AB=6cm
a. Tính tam giác vuông ABC
b. Vẽ đường cao AH và trung tuyến AM của tam giác ABC. Tính diện tích tam giác AHM
a: Ta có: ΔABC vuông tại A
nên \(\widehat{B}+\widehat{C}=90^0\)
hay \(\widehat{C}=60^0\)
Xét ΔABC vuông tại A có
\(AC=AB\cdot\tan30^0\)
\(=2\sqrt{3}\left(cm\right)\)
\(\Leftrightarrow BC=4\sqrt{3}\left(cm\right)\)
Cho tam giác ABC có AB = 6 cm ; AC = 4,5 cm ; BC = 7,5 cm a) chứng minh tam giác ABC vuông tại A b) Kẻ đường cao AH (H thuộc BC) tính BH, HC, AH và góc B,C của tam giác c) Tính diện tích tam giác ABC d) tìm vị trí điểm M để diện tích tam giác ABC bằng diện tích tam giác MBC
a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
c: \(S_{ABC}=\dfrac{AB\cdot AC}{2}=\dfrac{6\cdot4.5}{2}=3\cdot4.5=13.5\left(cm^2\right)\)
Cho tam giác vuông ABC, góc A = 90o, góc C = 30o và đường phân giác BD (D thuộc cạnh AC).
a) Tính tỉ số AD/CD.
b) Cho biết độ dài AB = 12,5cm. Hãy tính chu vi và diện tích của tam giác ABC.
a) + Δ ABC vuông tại A, có 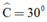
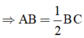
(Trong một tam giác vuông, cạnh đối diện với góc 30o bằng một nửa cạnh huyền)
+ Δ ABC có BD là phân giác của 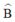
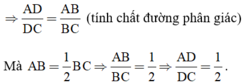
b) AB = 12,5cm ⇒ BC = 2AB = 2.12,5 = 25cm
Áp dụng định lí Py- ta- go vào tam giác ABC ta có:
AB2 + AC2 = BC2 nên AC2 = BC2 - AB2
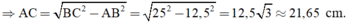
+ Chu vi tam giác ABC là:
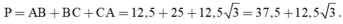
+ Diện tích tam giác ABC là:
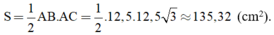
cho tam giác abc vuông tại a: bc=25,ah=12.
a. tính hc?
b. tính diện tích tam giác abc
Cho tam giác ABC góc A=90°AC=4cm Bc=5cm đường cao AH phân giác AD a, tính ac b, chứng minh tam giác ABC đồng giác với tam giác HAC c, AC²=HC.BC ; HB?HC? d, tính DC e, diện tích ABC , diện tích ABC Em cần gấp lắm ạ
a.Áp dụng định lý pitago:
\(AB=\sqrt{5^2-4^2}=\sqrt{9}=3\left(cm\right)\)
b.Xét tam giác ABC và tam giác HAC, có:
\(\widehat{BAC}=\widehat{AHC}=90^o\)
\(\widehat{C}\): chung
Vậy tam giác ABC đồng dạng tam giác HAC ( g.g )
\(\Rightarrow\dfrac{AC}{HC}=\dfrac{BC}{AC}\)
\(\Leftrightarrow AC^2=BC.HC\) ( đfcm )
c.\(\Rightarrow HC=\dfrac{AC^2}{BC}=\dfrac{4^2}{5}=3,2\left(cm\right)\)
\(HB=BC-HC=5-3,2=1,8\left(cm\right)\)
d.Áp dụng t/c đường phân giác \(\widehat{BAC}\) có:
\(\dfrac{AB}{AC}=\dfrac{DB}{DC}\)
\(\Leftrightarrow\dfrac{3}{4}=\dfrac{DB}{DC}\)
\(\Leftrightarrow\dfrac{DC}{4}=\dfrac{DB}{3}=\dfrac{DC+DB}{4+3}=\dfrac{5}{7}\)
\(\Rightarrow DC=\dfrac{5}{7}.4=\dfrac{20}{7}\left(cm\right)\)
e.\(S_{ABC}=\dfrac{1}{2}.AB.AC=\dfrac{1}{2}.3.4=6\left(cm^2\right)\)
Cho tam giác ABC có CosB=1/3 , AC=b đường cao hạ từ đỉnh B bằng tổng hai đường cao còn lại . Tính diện tích của tam giác ABC
cho tam giác ABC. Gọi AA' ;BB' ; CC' là các đường cao
a. Chứng minh tam giác ABC đồng dạng Tam giác AB'C'
b. Chứng minh AB' . BC' . CA' = AB . BC . CA . cosA . cosB .cosC
c. cho góc A =30 độ ; AB= 4cm; AC= 8cm tính diện tích tam giác ABC
cho tam giác ABC vuông tại A, BC=25 cm. đường cao AH=12 cm. a) tính HC b) tính diện tích tam giác ABC
Áp dụng hệ thức lượng ta có:
\(AH^2=BH.CH\)
\(\Rightarrow\)\(BH.CH=144\)
\(BH+CH=BC\)
\(\Rightarrow\)\(BH+CH=25\)
Theo hệ thức Vi-ét thì BH và CH là 2 nghiệm của phương trình:
\(x^2-25x+144=0\)
\(\Leftrightarrow\)\(\left(x-16\right)\left(x-9\right)=0\)
\(\Leftrightarrow\)\(\orbr{\begin{cases}x-16=0\\x-9=0\end{cases}}\)
\(\Leftrightarrow\)\(\orbr{\begin{cases}x=16\\x=9\end{cases}}\)
Vậy \(HC=16\)hoặc \(HC=9\)
p/s: mk k chắc cho lắm, bn tham khảo nhé
mk chưa hok đến vi ét bạn dùng cách khác đc ko ạ
Cách khác:
Ta tính được:
\(BH+CH=25\) \(\Rightarrow\)\(BH=25-CH\) (*)
\(BH.CH=144\) (1)
Thay (*) vào (1) ta được:
\(\left(25-CH\right).CH=144\)
\(\Leftrightarrow\)\(25.CH-CH^2=144\)
\(\Leftrightarrow\)\(CH^2-25.CH+144=0\)
\(\Leftrightarrow\)\(\left(CH-9\right)\left(CH-16\right)=0\)
\(\Leftrightarrow\)\(\orbr{\begin{cases}CH=9\\CH=16\end{cases}}\)