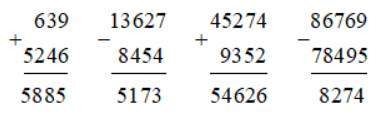(990 - 639) : 9 990 - 639 : 9

Những câu hỏi liên quan
tính
4/9 + 7/63
9 + 2/5
17/18 - 3/9
3 - 14/15
4/9 + 7/63 = 28/63 + 7/63 = 35/63
9 + 2/5 = 45/5 + 2/5 = 47/5
17/18 - 3/9 = 17/18 - 6/18 = 11/18
3 - 14/15 = 75/15 - 14/15 = 61/15
LY: Tự rút gọn (nếu cần)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Tính nhanh
325 x 780 x 5 - 639 :9
5 x 65 x 156 x 5 x 5 - 639 : 9
= 1267500 - 71
= 1267429
Đúng 0
Bình luận (0)
chứng minh rằng
E= \(\frac{9^{11}-9^{10}-9^9}{639}\) là số tự nhiênn
\(E=\frac{9^{11}-9^{10}-9^9}{639}\)
\(E=\frac{9^9\left(9^2-9-1\right)}{639}\)
\(E=\frac{9^2.71}{639}\)
\(E=\frac{9^2.71}{9.71}\)
\(E=9\)
Vậy E là 1 số tự nhiên
Đúng 0
Bình luận (0)
Chứng minh
a/ 81^7-27^9+3^29chia hết cho33
b/ [(9^11-9^10-9^9):639 thuộc N
c/ (36^36-9^2000) chia hết cho 45
a) Có 817 - 279 + 329
= (34)7 - (33)9 + 329
= 328 - 327 + 329
= 327(3 - 1 + 32)
= 327.11 = 326.33 \(⋮33\)
b) 911 - 910 - 99
= 99(92 - 9 - 1)
= 99.71
= 98.639 \(⋮639\)
c) P = 3636 - 92000
Có 3636 = \(\overline{....6}\)
\(9^{2000}=\left(9^2\right)^{1000}=81^{1000}=\overline{.....1}\)
nên P = \(\overline{...6}-\overline{...1}=\overline{...5}\Rightarrow P⋮5\)
dễ thấy P \(⋮9\) mà (5;9) = 1
nên \(P⋮9.5=45\)
Đúng 1
Bình luận (0)
Đặt tính rồi tính.
639 + 5 246 13 627 – 8 454
45 274 + 9 352 86 769 – 78 495
Kết quả bỏ ngoặc biểu thức sau:
A. -161 +413 – 187+ 639 - 200 B. 161 - 413 – 187+ 639 - 200
C. 161 +413 – 187+ 639 + 200 D. 161 +413 + 187+ 639 - 200
CMR :
E = \(\frac{9^{11}-9^{10}-9^9}{639}\) là số tự nhiên
giúp với
Ta có :
\(E=\frac{9^{11}-9^{10}-9^9}{639}\)
\(E=\frac{9^8\left(9^3-9^2-9\right)}{639}\)
\(E=\frac{9^8.639}{639}\)
\(E=9^8\)
Chúc bạn học tốt ~
Đúng 0
Bình luận (0)
Đặt B = 911 - 910 -99
B = 98. ( 93-92-9)
B =98. 639
Thay B vào A, có:
\(A=\frac{9^8.639}{639}=9^8\)
=> A là số tự nhiên ( đ p c m)
Đúng 0
Bình luận (0)
E = \(\frac{9^{11}-9^{10}-9^9}{639}\)
E = \(\frac{27506854719}{639}\)
E = 43046721
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
1 số nhân với 9 thì bằng 990. Vậy số đó là ...?
Gọi số đó là a, ta có:
a x 9 = 990
a = 990 : 9
a = 110
Vậy số đó là 110
!!!
Đúng 0
Bình luận (0)
a)\(\frac{9^{11}-9^{10}-9^9}{639}\)
b)\(\frac{\left(5^4-5^3\right)^3}{125^4}\)
\(\frac{9^{11}-9^{10}-9^9}{639}\)
\(=\frac{9^9\left(9^2-9-1\right)}{639}\)
\(=\frac{9^8\left(9^2-9-1\right)}{71}\)
\(=\frac{9^8.71}{71}\)
\(=9^8\)
Đúng 0
Bình luận (0)
\(\frac{\left(5^4-5^3\right)^3}{125^4}\)
\(\frac{\left[5^3.4\right]^3}{125^4}\)
\(\frac{5^9.4^3}{5^{12}}\)
\(\frac{4^3}{5^3}\)
Đúng 0
Bình luận (0)