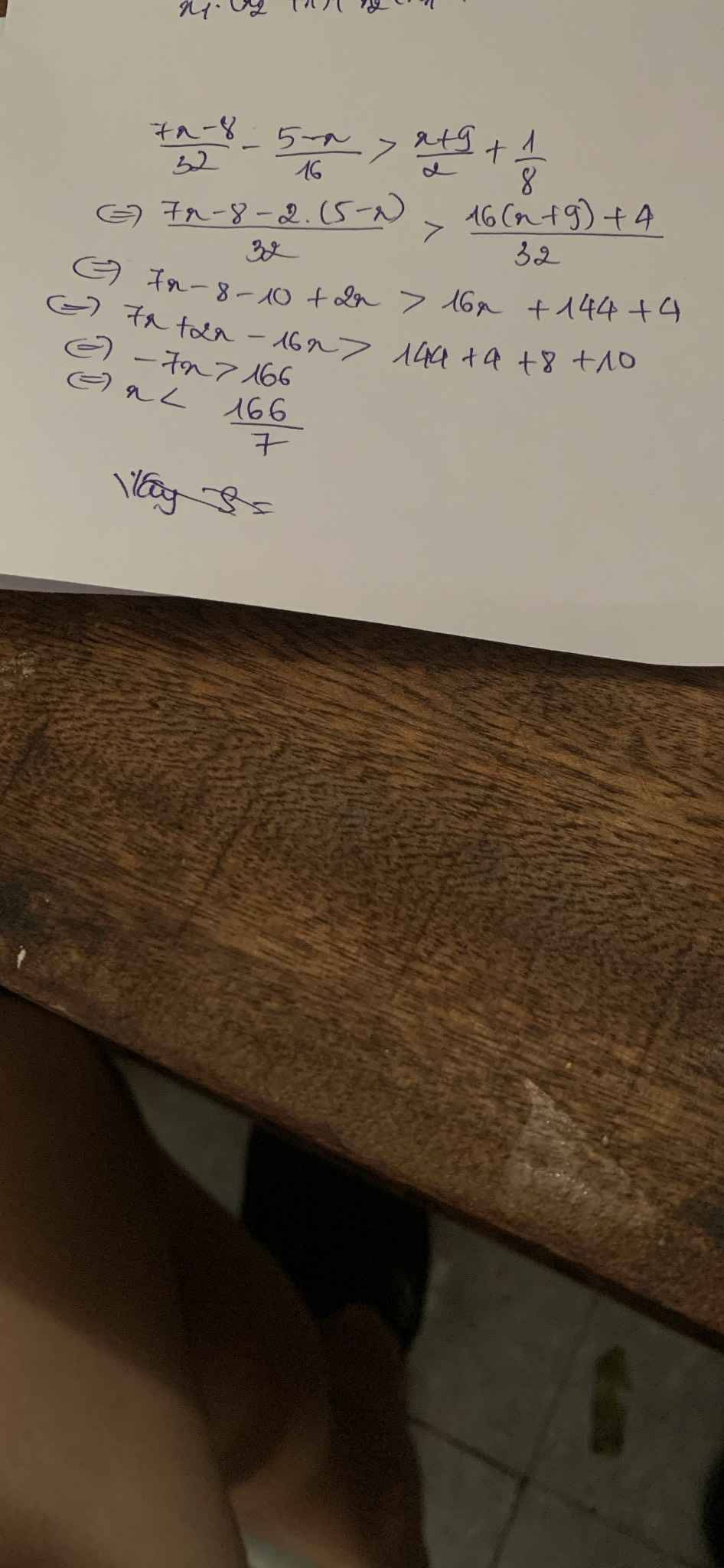lớp mấy

\(6\sqrt{x^2-34x+64}=x^2-34x+48\)

\(\text{đ}at:x^2-34x+48=a\Rightarrow6\sqrt{a+16}=a\Leftrightarrow36a+576=a^2\Leftrightarrow a^2-36a-576=0;\Delta=\left(-36\right)^2-4.\left(-576\right).1=3600\Rightarrow\left\{{}\begin{matrix}a_1=24\\a_2=-96\end{matrix}\right.\)

\(+,a=-96\Rightarrow x^2-34x+48=-96\Leftrightarrow x^2-34x+144=0;\Delta=34^2-4.144=580\Rightarrow\left\{{}\begin{matrix}x_1=-34+2\sqrt{145}\\x_2=-34-2\sqrt{145}\end{matrix}\right.\)

\(+,a=24\Rightarrow x^2-34x+48=24\Leftrightarrow x^2-34x+24=0;\Delta=1156-96=1060\Rightarrow\left\{{}\begin{matrix}x_1=-34+2\sqrt{265}\\x_2=-34-2\sqrt{265}\end{matrix}\right.\)

$a)\frac{2x}{2x^{2}-5x+3}+\frac{13x}{2x^{2}+x+3}=6$ (1)

Nhận thấy x=0 ko phải nghiệm của phương trình

Chia cả tử và mẫu của mỗi phân thức cho x, ta được:

$\frac{2}{2x-5+\frac{3}{x}}+\frac{13}{2x+1+\frac{3}{x}}=6$

Đặt $2x+\frac{3}{x}$=t

=> (1) <=> $\frac{2}{t-5}+\frac{13}{t+1}=6$

<=> $2t^{2}-13t+11=0$

Có a+b+c=2-13+11=0

=> $t_{1}=1$

$t_{2}=\frac{c}{a}=\frac{11}{2}$

* t = 1

=> $2x+\frac{3}{x}=1$

<=> $2x^{2}-x+3=0$ (vô nghiệm)

* t = $\frac{11}{2}$

=> $2x+\frac{3}{x}=\frac{11}{2}$

<=> $4x^{2}-11x+6=0$

=> $x_{1}=\frac{3}{4}$

$x_{2}=2$

Vậy phương trình có tập nghiệm S={$\frac{3}{4};2$}

b, \(x^2+\left(\dfrac{x}{x-1}\right)^2=1\)

\(\Leftrightarrow\left[x^2+\left(\dfrac{x}{x-1}\right)^2+2.x.\dfrac{x}{x-1}\right]-2.\dfrac{x^2}{x-1}-1=0\)

\(\Leftrightarrow\left(x+\dfrac{x}{x-1}\right)^2-2.\dfrac{x^2}{x-1}-1=0\)

\(\Leftrightarrow\left(\dfrac{x\left(x-1\right)+x}{x-1}\right)^2-2.\dfrac{x^2}{x-1}-1=0\)

\(\Leftrightarrow\left(\dfrac{x^2}{x-1}\right)^2-2.\dfrac{x^2}{x-1}-1=0\) (1)

Đặt : \(\dfrac{x^2}{x-1}=t\) (*) thì phương trình (1) trở thành:

\(t^2-2t-1=0\)

Ta có: \(\Delta=8>0\)

\(\Rightarrow t_1=\dfrac{2-\sqrt{8}}{2}=\dfrac{2-2\sqrt{2}}{2}=1-\sqrt{2}\)

\(t_2=\dfrac{2+\sqrt{8}}{2}=\dfrac{2+2\sqrt{2}}{2}=1+\sqrt{2}\)

Thay vào (*) rồi tìm x là xong

=.= hk tốt!!

suy ra x-2canx+1+y-6cany+9+z-8canz+16=0

suy ra [(canx)-1]^2 +[(cany-3)]^2 +[(canz-4)]=0

suy ra x=1,y=9,z=16

 16/căn của(x-3)+9/căn của(y-1)+1225/căn của(z-665)=84-căn của(x-3)-căn của(y-1)-căn của(z-665 
<=>[ 16/căn của(x-3) + căn của(x-3) ] + [ 9/căn của(y-1) + căn của(y-1)] + [1225/căn của(z-665)+căn của(z-665)] = 84 
cô si vế trái 
=> VT >= 2.4 + 2.3 + 2.35 = 84 = VP 
nếu mà là 82 thì pt vô nghiệm

gì đây?????

\(\Leftrightarrow\dfrac{7x-8}{32}-\dfrac{2\left(5-x\right)}{32}>\dfrac{16\left(x+9\right)}{32}+\dfrac{4}{32}\)

\(\Leftrightarrow7x-8-2\left(5-x\right)>16\left(x+9\right)+4\)

\(\Leftrightarrow7x-8-10+2x>16x+148\)

\(\Leftrightarrow-7x>166\)

\(\Rightarrow x< -\dfrac{166}{7}\)