Cho tam giác ABC vuông tại A . Gọi I là trung điểm của BC . Trên tia đối của tia IA lấy điểm o sao cho IB bằng IA
a, Chứng minh tam giác BID bằng tam giác CIA
b, Chứng minh BD vuông góc với AB
Mọi người kẻ hình ra giúp mk nha ^_^
Cho tam giác ABC vuông tại A. Gọi I là trung điểm BC. Trên tia đối của tia IA lấy điểm
D sao cho ID = IA
a) CMR: T.giác BID = T.giác CIA
b) CMR: BD V.góc với AB
c) Qua A kẻ đường thẳng song song với BC cắt đường thẳng BD tại M. Chứng minh T.giác BAM = T.giác ABC
a: Xét ΔBID và ΔCIA có
IB=IC
\(\widehat{BID}=\widehat{CIA}\)
ID=IA
Do đó: ΔBID=ΔCIA
b: Xét tứ giác ABDC có
I là trung điểm của AD
I là trung điểm của BC
Do đó: ABDC là hình bình hành
mà \(\widehat{BAC}=90^0\)
nên ABDC là hình chữ nhật
Suy ra: BD\(\perp\)AB
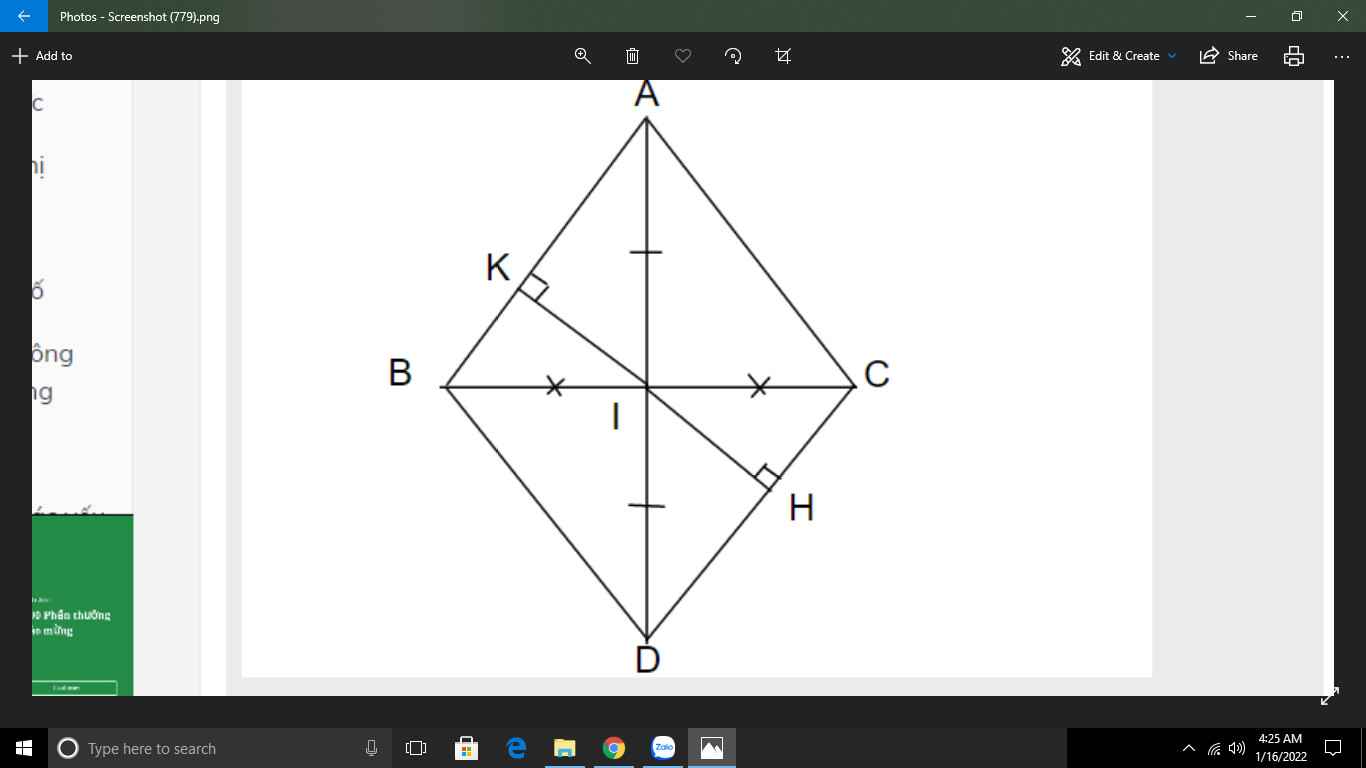
Cho tam giác ABC có AB = AC. Gọi I là trung điểm của BC, trên tia đối của tia IA lấy điểm D sao cho ID = IA
a) Chứng minh tam giác ABI = tam giác ACI
b) Chứng minh AC // BD
c) Kẻ IK vuông góc với AB (K ϵ AB), IH vuông góc với CD (H ϵ CD). Chứng minh IK= IH
\(\text{a)}\text{Xét }\Delta ABI\text{ và }\Delta ACI\text{ có:}\)
\(AB=AC\left(gt\right)\)
\(BI=CI\text{(I trung điểm BC)}\)
\(AI\text{ chung}\)
\(\Rightarrow\Delta ABI=\Delta ACI\left(c.c.c\right)\)
\(\text{b)Xét }\Delta AIC\text{ và }\Delta DIB\text{ có:}\)
\(AI=DI\left(gt\right)\)
\(\widehat{AIC}=\widehat{DIB}\text{(đối đỉnh)}\)
\(IC=IB\)
\(\Rightarrow\Delta AIC=\Delta DIB\left(c.g.c\right)\)
\(\Rightarrow\widehat{DIB}=\widehat{ICA}\text{(2 góc tương ứng)}\)
\(\text{mà chúng so le trong}\)
\(\Rightarrow AC=BD\)
\(\text{c)Xét }\Delta IKB\text{ và }\Delta IHC\text{ có:}\)
\(\widehat{IKB}=\widehat{IHC}=90^0\)
\(IB=IC\)
\(\widehat{KIB}=\widehat{CIH}\text{(đối đỉnh)}\)
\(\Rightarrow\Delta IKB=\Delta IHC\left(ch-gn\right)\)
\(\Rightarrow IK=IH\)
\(\text{Hình có chỗ nào bạn ko thấy rõ thì ib riêng cho mik nghe:3}\)
cho tam giác ABC VUÔNG Tại A . gọi I là trung điểm của bc . trên tia đối của IA lấy điểm D sao chi ID=Ia
a) chứng minh rằng tam giá BID = tam giác CIA
b) CMR BD vuông góc AB
c) qua a kẻ đường song song với BC cắt đường thẳng BD tại M. chứng minh. tam giác BAM= tam giác ABC
d) chứng minh rằng AB là phân giác của góc DAM
Mình vẽ nhầm hình nha, để mình vẽ lại ở dưới cái nào để chữ vẽ lại thì bạn vẽ cái đó
Đây là bài làm
a) Δ BID và Δ CIA có:
ID=IB (gt)
DIB=CIA (đói đỉnh)
IA=ID (gt)
=> Δ BID=Δ CIA (c.g.c)
b) Ta có: AM // BC
=> MAB=CAB (so le trong)
Δ BID=Δ CIA (cmt)
=> BDI=CAI ( 2 góc tương ứng)
và chúng ở vị trí so le trong
=> CA // DM
Ta có: CA // DM (cmt)
=> CAB=MBA=900 (so le trong)
Δ BAM và Δ ABC có:
MAB=CAB (cmt)
BA cạnh chung
CAB=MBA=900 (cmt)
=> Δ BAM=Δ ABC (g.c.g)
c)Δ BAM=Δ ABC
=> BM=AC (2 cạnh tương ứng)
Mà AC=BD ( Δ BID=Δ CIA)
=>BM=BD
MBA=900 (cmt)
mà MBA+ABD=1800 ( kề bù)
900 +ABD=1800
=>ABD=1800-900=900
=>MBA=ABD
Δ ADB=Δ AMB có:
BM=BD (cmt)
MBA=ABD (cmt)
AB cạnh chung
=> Δ ADB=Δ AMB ( g.c.g)
=>MAB=DAB (2 góc tương ứng)
Vậy AB là phân giác góc DAM
@Trần Nghiên Hy mk đang quen cách làm của lớp 8 rồi, chả nhớ j lớp 7 cả
a. Xét tam giác BID và tam giác CID có :
AI=ID ( giả thiết )
BI=CI ( vì I là trung điểm của BC )
góc BID=góc CIA ( đối đỉnh )
Nên tam giác BID= tam giác CIA ( c- g- c)
b.
Bài 1 :
Cho ABC nhọn (AB < AC). Gọi M là trung điểm của BC. Trên tia AM lấy đi ểm N sao cho M là trung điểm của AN.
a/. Ch/m : ΔAMB = ΔNMC
b/. Vẽ CD \bot AB (D\in AB). So sánh góc ABC và góc BCN. Tính góc DCN.
c/. Vẽ AH \bot BC (H \in BC), trên tia đối của tia HA lấy điểm I sao cho HI = HA.
Ch/m : BI = CN.
BÀI 2 :
Vẽ góc nhọn xAy. Trên tia Ax lấy hai điểm B và C (B nằm giữa A và C). Trên tia Ay lấy hai điểm D và E sao cho AD = AB; AE = AC
a) Chứng minh BE = DC
b) Gọi O là giao điểm BE và DC. Chứng minh tam giác OBC bằng tam giác ODE.
c) Vẽ trung điểm M của CE. Chứng minh AM là đường trung trực của CE.
Bài 3
Cho tam giác ABC ( AB< AC ) . Gọi I là trung điểm của AC. Trên tia đối của tia IB lấy điểm D, sao cho IB = ID. Chứng minh :
a) Tam giác AIB bằng tam giác CID.
b) AD = BC v à AD // BC.
Bài 4.
Cho tam giác ABC ( AB< AC ) . Gọi I là trung điểm của AC. Trên tia đối của tia IB lấy điểm D, sao cho IB = ID. Chứng minh :
a) Tam giác AIB bằng tam giác CID.
b) AD = BC v à AD // BC.
Bài 4.
Cho tam giác ABC ( AB< AC ) . Gọi I là trung điểm của AC. Trên tia đối của tia IB lấy điểm D, sao cho IB = ID. Chứng minh :
a) Tam giác AIB bằng tam giác CID.
b) AD = BC v à AD // BC.
BÀI 4
Cho tam giác ABC có góc A =350 . Đường thẳng AH vuông góc với BC tại H. Trên đường vuông góc với BC tại B lấy điểm D không cùng nửa mặt phẳng bờ BC với điểm A sao cho AH = BD.
a) Chứng minh ΔAHB = ΔDBH.
b) Chứng minh AB//HD.
c) Gọi O là giao điểm của AD và BC. Chứng minh O là trung điểm của BH.
d) Tính góc ACB , biết góc BDH= 350 .
Bài 5 :
Cho tam giác ABC cân tại A và có \widehat{A}=50^0 .
Tính \widehat{B} và \widehat{C}
Lấy D thuộc AB, E thuộc AC sao cho AD = AE. Chứng minh : DE // BC.
Bài 6 :
Cho tam giác ABC cân tại A. Lấy D thuộc AC, E thuộc AB sao cho AD = AE.
Chứng minh : DB = EC.
Gọi O là giao điểm của BD và EC. Chứng minh : tam giác OBC và ODE là tam giác cân.
Chứng minh rằng : DE // BC.
Bài 7
Cho tam giác ABC. Tia phân giác của góc C cắt AB tại D. trên tia đối của tia CA lấy điểm E sao cho CE = CB.
Chứng minh : CD // EB.
Tia phân giác của góc E cắt CD tại F. vẽ CK vuông góc EF tại K. chứng minh : CK Tia phân giác của góc ECF.
Bài 8 :
Cho tam giác ABC vuông tại A có \widehat{B}=60^0 . Vẽ Cx vuông góc BC, trên tia Cx lấy điểm E sao cho CE = CA (CE , CA nằm cùng phía đối BC). trên tia đối của tia BC lấy điểm F sao cho BF = BA. Chứng minh :
Tam giác ACE đều.
A, E, F thẳng hàng.
Bài 3:
a: Xét ΔAIB và ΔCID có
IA=IC
góc AIB=góc CID
IB=ID
Do đó: ΔAIB=ΔCID
b: Xét tứ giác ABCD có
I là trung điểm chung của AC và BD
nên ABCD là hình bình hành
Suy ra: AD//BC va AD=BC
Bài 6:
a: Xét ΔADB và ΔAEC có
AD=AE
góc A chung
AB=AC
Do đó: ΔADB=ΔAEC
SUy ra: BD=CE
b: Xét ΔEBC và ΔDCB có
EB=DC
BC chung
EC=BD
Do đó: ΔEBC=ΔDCB
Suy ra: góc OBC=góc OCB
=>ΔOBC cân tại O
=>OB=OC
=>OE=OD
=>ΔOED cân tại O
c: Xét ΔABC có AE/AB=AD/AC
nên ED//BC
cho tam giác ABC vuông tại A.có I là trung điểm của BC.trên tia đối của IA lấy điểm D sao cho ID=IA
a,chứng minh tam giác BID=tam giác CIA
b,chứng minh BD vuông góc AD
c,qua A kẻ đường thẳng song song với BC cắt BD tại M.chứng minh tam giác BAM=tam giác ABC
d,chứng minh AB là tia phan giac của góc DAM
Câu hỏi của Vy Hà Khánh - Toán lớp 7 - Học toán với OnlineMath
Em tham khảo nhé!
Cho tam giác ABC vuông tại A. Gọi I là trung điểm BC. Trên tia đối của tia IA lấy điểm D sao cho ID=IA
a) CMR tam giác BID bằng tam giác CIA
b) CMR : BD vuông góc với AB
c) Qua A kẻ đường thẳng song song với BC cắt đường thẳng BD tại M. C/M tam giác BAM bằng tam giác ABC
d) CMR: AB là tia phân giác cuả góc DAM
Em tham khảo nhé!
Câu hỏi của Vy Hà Khánh - Toán lớp 7 - Học toán với OnlineMath
Cho tam giác BC vuông tại A .Gọi I là trung điểm BC .Trên tia đối cỉa tia IA lấy điểm D sao cho ID =IA
a) CM tam giác BID =tam giác CIA
b) CM BD vuông góc AB
c) Qua A kẻ đường thẳng song song với BC cắt đường thẳng BD tại M .Chứng minh rằng tam giác BAM= tam giác ABC
d) CM : AB là tia phân giác của góc DAM
cho tam giác ABC gọi I là trung điểm của BC, biết rằng AI vuông góc với BC
a). Chứng minh: tam giác ABI = tam giác ACI
b). Chứng minh: tam giác ABC cân tại A
c). Trên tia đối của tia IA lấy điểm D sao cho ID = IA. Chứng minh: AB // CD
a: Xét ΔABI vuông tại I và ΔACI vuông tại I có
AI chung
BI=CI
Do đó: ΔABI=ΔACI
b: Ta có: ΔABI=ΔACI
nên AB=AC
hay ΔABC cân tại A
c: Xét tứ giác ABDC có
I là trung điểm của BC
I là trung điểm của AD
Do đó:ABDC là hình bình hành
Suy ra: AB//CD
1. Cho tam giác ABC vuông tại A. tia phân giác góc B cắt AC tại D. từ A kẻ AE vuông góc BD tại E và cắt BC tại M
A. chứng minh tam giác ABC bằng tam giác MBE
B. chứng minh DM vuông góc với BC
C .Kẻ AH vuông góc với BC tại I. Chứng minh AM là tia phân giác của góc IAC
câu 2: Cho tam giác ABC cân tại A (góc A bé hơn 90 độ). vẽ tia phân giác AD của góc A (D thuộc BC)
A. chứng minh tam giác ABD bằng tam giác ACD
B. Vẽ đường trung tuyến của tam giác ABC cắt cạnh AC tại G. chứng minh G là trọng tâm của tam giác ABC
C. Gọi H là trung điểm của cạnh DC. qua h Vẽ đường thẳng vuông góc với cạnh DC cắt cạnh AC tại E. Chứng minh tam giác DEC cân
D. Chứng minh ba điểm B, G, E thẳng hàng
Câu 3 Cho tam giác ABC vuông tại A. Vẽ trung tuyến AM của tam giác ABC, Kẻ MH vuông góc với AC. Trên tia đối của tia MH đặt điểm K sao cho MK bằng MH
a. chứng minh tam giác MHC bằng tam giác MKB và BK vuông góc với KH
B. Chứng minh AB song song với HK và BK = AH.
C. Vẽ BH cắt AB tại g. Gọi I là trung điểm của AB. Chứng minh ba điểm C, G, I thẳng hàng
câu4 Cho tam giác ABC vuông tại A. gọi M là trung điểm cạnh BC. trên tia đối của tia MA lấy điểm D sao cho MD = MA.
A . chứng minh tam giác MCD bằng tam giác MBD và AC song song với BD
B. Gọi I là trung điểm AM, J là trung điểm BM. AJ cắt BI tại G. Chứng minh tam giác GAB là tam giác cân
Câu 5 cho tam giác ABC vuông tại A (AB bé hơn AC). vẽ BD là tia phân giác của góc ABC (D thuộc AC). trên đoạn BC lấy điểm E sao cho BE bằng BA
a chứng minh tam giác ABD bằng tam giác EBD .Từ đó suy ra góc BED là góc vuông
b. tia ED cắt tia BA tại EF. Chứng minh tam giác BED cân
C. Chứng minh tam giác AFC bằng tam giác ECF
D.Chứng minh: AB + AC >DE+BC
câu 6: Cho tam giác ABC vuông tại A. Vẽ đường phân phân giác BD của tam giác ABC và E là hình chiếu của D trên BC
a. chứng minh tam giác ABD bằng tam giác EBD và AE vuông góc với BD
B. Gọi giao điểm của hai đường thẳng ED và BA là F. Chứng minh tam giác ABC bằng tam giác AFC
C. Qua A vẽ đường thẳng vuông góc với BC cắt CF tại G. Chứng minh ba điểm B, D, G thẳng hàng
câu 7: Cho tam giác ABC cân tại A (góc A bé hơn 90 độ). vẽ AD là phân giác của góc A (D thuộc BC)
A . Chứng minh tam giác ABD bằng tam giác ACD
B. lấy H là trung điểm của AB. Trên tia đối của tia HC lấy điểm K sao cho HK = HC. Chứng minh rằng AK = BC
c. CH cắt AD tại G. Chứng minh (BA+BC)÷6 >GH
Ta có: ΔABC đều, D ∈ AB, DE⊥AB, E ∈ BC
=> ΔBDE có các góc với số đo lần lượt là: 300
; 600
; 900
=> BD=1/2BE
Mà BD=1/3BA => BD=1/2AD => AD=BE => AB-AD=BC-BE (Do AB=BC)
=> BD=CE.
Xét ΔBDE và ΔCEF: ^BDE=^CEF=900
; BD=CE; ^DBE=^ECF=600
=> ΔBDE=ΔCEF (g.c.g) => BE=CF => BC-BE=AC-CF => CE=AF=BD
Xét ΔBDE và ΔAFD: BE=AD; ^DBE=^FAD=600
; BD=AF => ΔBDE=ΔAFD (c.g.c)
=> ^BDE=^AFD=900
=>DF⊥AC (đpcm).
b) Ta có: ΔBDE=ΔCEF=ΔAFD (cmt) => DE=EF=FD (các cạnh tương ứng)
=> Δ DEF đều (đpcm).
c) Δ DEF đều (cmt) => DE=EF=FD. Mà DF=FM=EN=DP => DF+FN=FE+EN=DE+DP <=> DM=FN=EP
Lại có: ^DEF=^DFE=^EDF=600=> ^PDM=^MFN=^NEP=1200
(Kề bù)
=> ΔPDM=ΔMFN=ΔNEP (c.g.c) => PM=MN=NP => ΔMNP là tam giác đều.
d) Gọi AH; BI; CK lần lượt là các trung tuyến của ΔABC, chúng cắt nhau tại O.
=> O là trọng tâm ΔABC (1)
Do ΔABC đều nên AH;BI;BK cũng là phân giác trong của tam giác => ^OAF=^OBD=^OCE=300
Đồng thời là tâm đường tròn ngoại tiếp tam giác => OA=OB=OC
Xét 3 tam giác: ΔOAF; ΔOBD và ΔOCE:
AF=BD=CE
^OAF=^OBD=^OCE => ΔOAF=ΔOBD=ΔOCE (c.g.c)
OA=OB=OC
=> OF=OD=OE => O là giao 3 đường trung trực Δ DEF hay O là trọng tâm Δ DEF (2)
(Do tam giác DEF đề )
/
(Do tam giác DEF đều)
Dễ dàng c/m ^OFD=^OEF=^ODE=300
=> ^OFM=^OEN=^ODP (Kề bù)
Xét 3 tam giác: ΔODP; ΔOEN; ΔOFM:
OD=OE=OF
^ODP=^OEN=^OFM => ΔODP=ΔOEN=ΔOFM (c.g.c)
OD=OE=OF (Tự c/m)
=> OP=ON=OM (Các cạnh tương ứng) => O là giao 3 đường trung trực của ΔMNP
hay O là trọng tâm ΔMNP (3)
Từ (1); (2) và (3) => ΔABC; Δ DEF và ΔMNP có chung trọng tâm (đpcm).