Trong hệ trục tọa độ Oxy, cho A(5;3), B(2;-4). Chứng minh: A, B, O tạo thành tam giác. Tính chu vi tam giác OAB.

Những câu hỏi liên quan
trong hệ trục tọa độ Oxy cho điểm A(2;3).Tọa độ của điểm B sao cho trục Ox là đường trung trực của đoạn thẳng AB
trong hệ trục tọa độ oxy cho A(1;2) B(-1;1) C(5;-1) tìm M sao cho |vectoMA + vectoMB + vectoMC | min
1. Trong hệ trục tọa độ Oxy có A(2;3) B(1;4), C(-1;-5)
tìm tọa độ điểm I trên AB sao cho \(\left|\overrightarrow{IA}+3\overrightarrow{IB}+5\overrightarrow{IC}\right|\) có giá trị nhỏ nhất
\(\overrightarrow{AB}=\left(-1;1\right)\) nên pt AB có dạng:
\(1\left(x-2\right)+1\left(y-3\right)=0\Leftrightarrow x+y-5=0\)
Do I thuộc AB nên tọa độ có dạng: \(I\left(a;5-a\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{IA}=\left(2-a;a-2\right)\\\overrightarrow{IB}=\left(1-a;a-1\right)\\\overrightarrow{IC}=\left(-1-a;a-10\right)\end{matrix}\right.\)
\(\Rightarrow\overrightarrow{IA}+3\overrightarrow{IB}+5\overrightarrow{IC}=\left(-9a;9a-55\right)\)
\(\Rightarrow\left|\overrightarrow{IA}+3\overrightarrow{IB}+5\overrightarrow{IC}\right|=\sqrt{\left(9a\right)^2+\left(55-9a\right)^2}\ge\sqrt{\dfrac{1}{2}\left(9a+55-9a\right)^2}=\dfrac{55}{\sqrt{2}}\)
Dấu "=" xảy ra khi \(9a=55-9a\Rightarrow a=\dfrac{55}{18}\Rightarrow I\left(\dfrac{55}{18};\dfrac{35}{18}\right)\)
Kiểm tra lại tính toán
Đúng 2
Bình luận (0)
trong hệ tọa độ Oxy , cho 2 điểm A( 2;2 ) và B( 1;5 ) . tìm tọa độ điểm M trên trục tung sao cho độ dài MA + MB nhỏ nhất
Trong mặt phẳng với hệ tọa độ Oxy, cho A(4 ; 5 ) , B( 6;7). Viết phương trình đường trung trục của AB
Trung điểm I của AB là: \(I\left(5;6\right)\)
Ta gọi pt đường thẳng AB có dạng: \(y=ax+b\)
\(\rightarrow\left\{{}\begin{matrix}5=a.4+b\\7=a.6+b\end{matrix}\right.\rightarrow\left\{{}\begin{matrix}a=1\\b=1\rightarrow\end{matrix}\right.AB:y=x+1\)
Gọi pt đường trung trực của AB là: \(y=ax+b\left(1\right)\)
Do (d) vuông góc với AB và d đi qua I nên:
\(\rightarrow\left\{{}\begin{matrix}a.1=-1\\6=a.4+b\end{matrix}\right.\)\(\rightarrow\left\{{}\begin{matrix}a=-1\\b=10\end{matrix}\right.\)\(\rightarrow\left(d\right):y=-x+10\)
Trong hệ tọa độ Oxy, cho hai điểm A(2; -3); B (3; 4) Tìm tọa độ điểm M thuộc trục hoành sao cho A, B, M thẳng hàng. A. M (1 ; 0) B. M(4; 0) C.
M
−
5
3
;
−
1
3
.
D.
M
17
7
;
0...
Đọc tiếp
Trong hệ tọa độ Oxy, cho hai điểm A(2; -3); B (3; 4) Tìm tọa độ điểm M thuộc trục hoành sao cho A, B, M thẳng hàng.
A. M (1 ; 0)
B. M(4; 0)
C. M − 5 3 ; − 1 3 .
D. M 17 7 ; 0 .
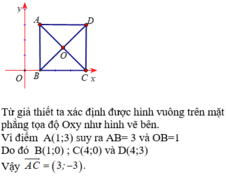
Trong hệ trục tọa độ Oxy, cho hình vuông ABCD tâm I và có A(1;3) . Biết điểm B thuộc trục Ox và
B
C
→
cùng hướng với
i
→
. Tìm tọa độ các vectơ
A
C
→
? A.(1;2) B.(3;4) C.(3;-3) D.(3;0)
Đọc tiếp
Trong hệ trục tọa độ Oxy, cho hình vuông ABCD tâm I và có A(1;3) . Biết điểm B thuộc trục Ox và B C → cùng hướng với i → . Tìm tọa độ các vectơ A C → ?
A.(1;2)
B.(3;4)
C.(3;-3)
D.(3;0)
Trong mặt phẳng với hệ trục tọa độ Oxy, cho 2 điểm A91;2) và B(4;3). Tìm tọa độ điểm M trên trục hoành sao cho góc AMB bằng 45 độ.
Giả sử tọa độ M(x;0). Khi đó \(\overrightarrow{MA}=\left(1-x;2\right);\overrightarrow{MB}=\left(4-x;3\right)\)
Theo giả thiết ta có \(\overrightarrow{MA}.\overrightarrow{MB}=MA.MB.\cos45^0\)
\(\Leftrightarrow\left(1-x\right)\left(4-x\right)+6=\sqrt{\left(1-x\right)^2+4}.\sqrt{\left(4-x\right)^2+9}.\frac{\sqrt{2}}{2}\)
\(\Leftrightarrow x^2-5x+10=\sqrt{x^2-2x+5}.\sqrt{x^2-8x+25}.\frac{\sqrt{2}}{2}\)
\(\Leftrightarrow2\left(x^2-5x+10\right)^2=\left(x^2-5x+10\right)\left(x^2-8x+25\right)\) (do \(x^2-5x+10>0\))
\(\Leftrightarrow x^4-10x^3+44x^2-110x+75=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-5\right)\left(x^2-4x+15\right)=0\)
\(\Leftrightarrow x=1;x=5\)
Vậy ta có 2 điểm cần tìm là M(1;0) hoặc M(5;0)
Đúng 2
Bình luận (0)
Trong hệ trục tọa độ Oxy, cho tam giác ABC có A(1;-5), B(2;1) và C(13;-8). Tính diện tích S của tam giác ABC
Help me!!!
\(S=\dfrac{1}{2}\left|\left(x_B-x_A\right)\left(y_C-y_A\right)-\left(x_C-x_A\right)\left(y_B-y_A\right)\right|\)
\(=\dfrac{1}{2}\left|\left(2-1\right)\left(-8+5\right)-\left(13-1\right)\left(1+5\right)\right|=\dfrac{75}{2}\)
Đúng 0
Bình luận (0)
Trong hệ trục tọa độ Oxy cho A (-3,1). Tìm điểm M thuộc Oy sao cho MA=2
M thuộc Oy nên M(0;y)
\(MA=2\)
=>\(\sqrt{\left(-3-0\right)^2+\left(1-y\right)^2}=2\)
=>(y-1)^2+9=4
=>(y-1)^2=-5(loại)
=>
Đúng 0
Bình luận (0)