CM: X^2+Y^2+X^2*Y^2+1=4*X*Y giải bằng bất đẳng thức cosi

Những câu hỏi liên quan
Cm bất đẳng thức sau vs x, y, z>_0
4(x^2+y^2+z^2)>_(x+y)^2+(y+z)^2+(z+x)^2
Biến đổi tương đương:
\(\Leftrightarrow4x^2+4y^2+4z^2\ge2x^2+2y^2+2z^2+2xy+2yz+2zx\)
\(\Leftrightarrow2x^2+2y^2+2z^2-2xy-2yz-2zx\ge0\)
\(\Leftrightarrow\left(x-y\right)^2+\left(y-z\right)^2+\left(z-x\right)^2\ge0\) (luôn đúng)
Dấu "=" xảy ra khi \(x=y=z\)
Đúng 0
Bình luận (0)
A no thơ quay nhưng lại không hay:P(Another way)
\(BĐT\Leftrightarrow x^2+y^2+z^2\ge xy+yz+zx\) (biến đổi tương đương thôi)
\(\Leftrightarrow\frac{3}{4}\left(x-y\right)^2+\frac{1}{4}\left(x+y-2z\right)^2\ge0\) (true)
Đẳng thức xảy ra khi x =y = z
P/s: cách này làm màu thôi :D
Đúng 0
Bình luận (0)
Thực ra mấy dạng bậc 2 kiểu này theo em thì dùng công thức \(at^2+bt+c=a\left(t+\frac{b}{2a}\right)^2+\frac{4ac-b^2}{4a}\) (bằng cách đưa về đa thức biến t)
Chi tiết như sau:(sai chỗ nào bl cho em biết cái nha:D)
BĐT \(\Leftrightarrow x^2+y^2+z^2\ge xy+yz+zx\)
\(\Leftrightarrow x^2-x\left(y+z\right)+y^2+z^2-yz\ge0\)
\(\Leftrightarrow\left(x-\frac{y+z}{2}\right)^2+\frac{4\left(y^2+z^2-yz\right)-\left(y+z\right)^2}{4}\ge0\)
\(\Leftrightarrow\frac{1}{4}\left(2x-y-z\right)^2+\frac{3}{4}\left(y-z\right)^2\ge0\)
Đúng 0
Bình luận (0)
Dùng phương pháp bất đẳng thức để giải phương trình sau (x^2+1)(y^2+4)(z^2+9)=48xyz(x;y;z>0)
Em học lớp 6 vào chtt nha tick cho em với
Đúng 0
Bình luận (0)
Chứng mình bất đẳng thức
1/\(\frac{1}{4}\left(\frac{x}{y}+\frac{y}{z}\right)\ge\frac{x}{y+z}\)
2/\(\frac{1}{x}+\frac{1}{y}\ge\frac{4}{x+y}\)
Mình mới làm quen với bất đẳng thức, các bạn giải chi tiết hộ mình nha. À mà giải theo Cauchy ý nha !
2)\(\frac{x+y}{xy}\ge\frac{4}{x+y}\Leftrightarrow\left(x+y\right)^2\ge4xy\)
theo yêu cầu của bạn thì đến đâ mk làm theo cách này
ÁP Dụng cô si ta có:\(x+y\ge2\sqrt{xy}\)\(\Rightarrow\left(x+y\right)^2\ge4xy\)(luôn đúng)\(\Rightarrowđpcm\)
cách 2
\(\left(x+y\right)^2\ge4xy\Leftrightarrow x^2+2xy+y^2\ge4xy\)
\(\Leftrightarrow x^2-2xy+y^2\ge0\Leftrightarrow\left(x-y\right)^2\ge0\)(luôn đúng)
\(\Rightarrowđpcm\)
Đúng 0
Bình luận (0)
chứng minh bất đẳng thức x^2*(1+y^2)+y^2*(1+z^2)+z^2*(x+x^2)> hoặc bằng 6xyz
x2+y2z2>=2lxl.lyl.lzl nên VT>=6lxl.lyl.lzl>=6xyz
Đúng 0
Bình luận (0)
chứng minh bất đẳng thức x^2*(1+y^2)+y^2*(1+z^2)+z^2*(x+x^2)> hoặc bằng 6xyz
Với x,y,z dương. Không sử dụng bất đẳng thức Cosi. C/m biểu thức sau
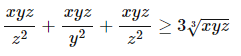
Cm bất đẳng thức sau vs x, y, z>_0.
3(x^2+y^2+z^2)>_(x+y+z)^2
Biến đổi tương đương:
\(3x^2+3y^2+3z^2\ge x^2+y^2+z^2+2xy+2yz+2zx\)
\(\Leftrightarrow2x^2+2y^2+2z^2-2xy-2yz-2zx\ge0\)
\(\Leftrightarrow\left(x-y\right)^2+\left(y-z\right)^2+\left(z-x\right)^2\ge0\) (luôn đúng)
Dấu "=" xảy ra khi \(x=y=z\)
Đúng 0
Bình luận (0)
Chứng minh đẳng thức, bất đẳng thức: \(x^4+y^4+\left(x+y\right)^4=2.\left(x^2+xy+y^2\right)^2\)
Lời giải:
Ta có:
$x^4+y^4+(x+y)^4=(x^4+y^4+2x^2y^2)-2x^2y^2+[(x+y)^2]^2$
$=(x^2+y^2)^2-2x^2y^2+(x^2+2xy+y^2)^2$
$=(x^2+y^2)^2-2x^2y^2+(x^2+y^2)^2+(2xy)^2+4xy(x^2+y^2)$
$=2(x^2+y^2)^2+2x^2y^2+4xy(x^2+y^2)$
$=2[(x^2+y^2)^2+2xy(x^2+y^2)+(xy)^2]$
$=2(x^2+y^2+xy)^2$
Ta có đpcm.
Giải giup giùm em em cần gấp ạ nghĩ mãi mà vẫn không ra
a)CM: 3(a^2+b^2+c^2)>=(a+b+c)^2 với a,b,c bất kỳ
b) Cho x>0,y>0,z>0 và x+y+z=1.CM:(x+1/x)^2+(y+1/y)^2+(z+1/z)^2>=100/3
Xác định giá trị nhỏ nhất của các biểu thức:
a)A=4x^2+9/x với x thay đổi, x>0
b) B= x^2+2y^2+3x-y+6 với x,y thay đổi
CM bất đẳng thức sau: a^2b^2+b^2c^2+c^2a^2>= abc(a+b+c) (a,b,c bất kỳ)

















