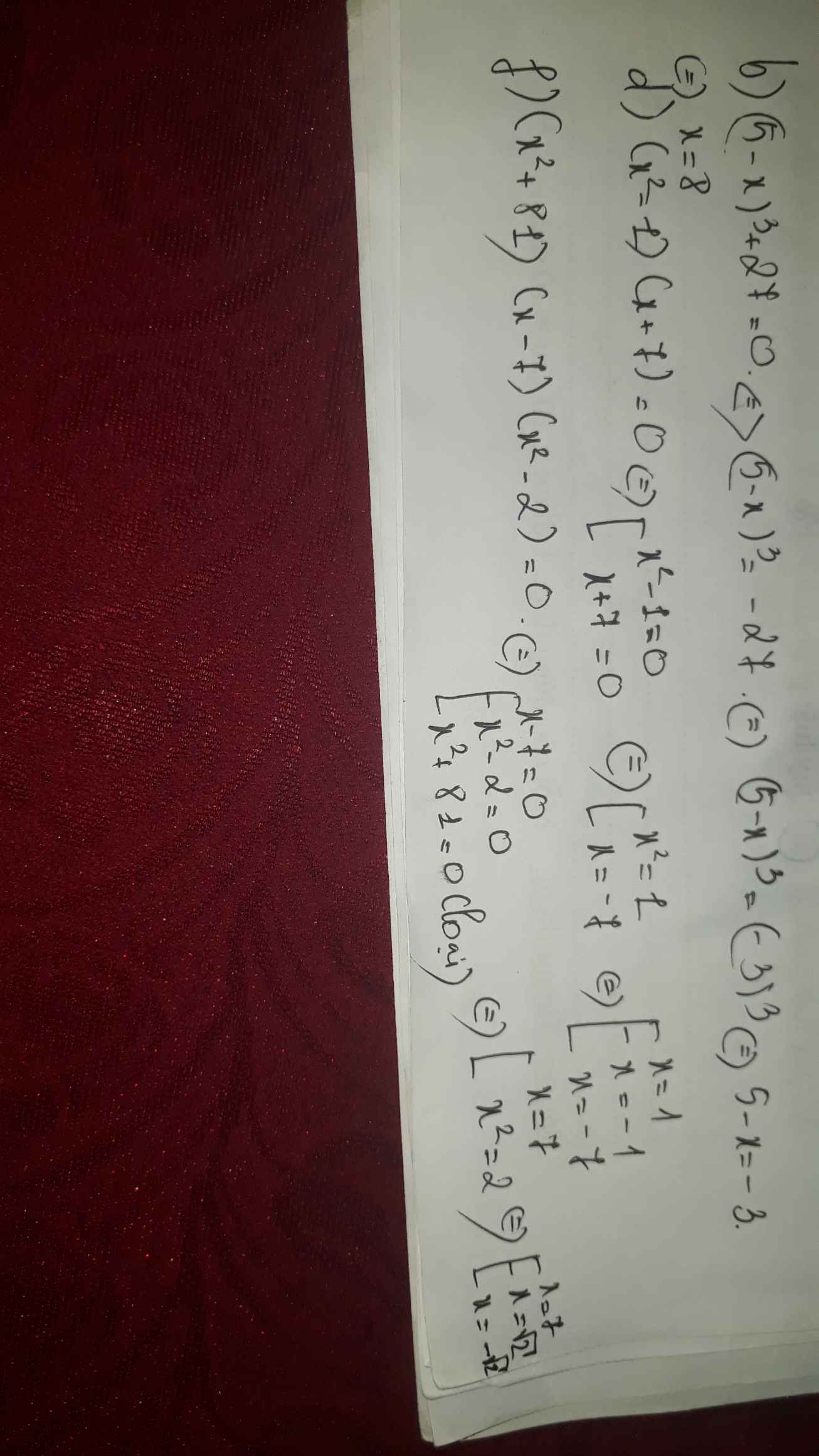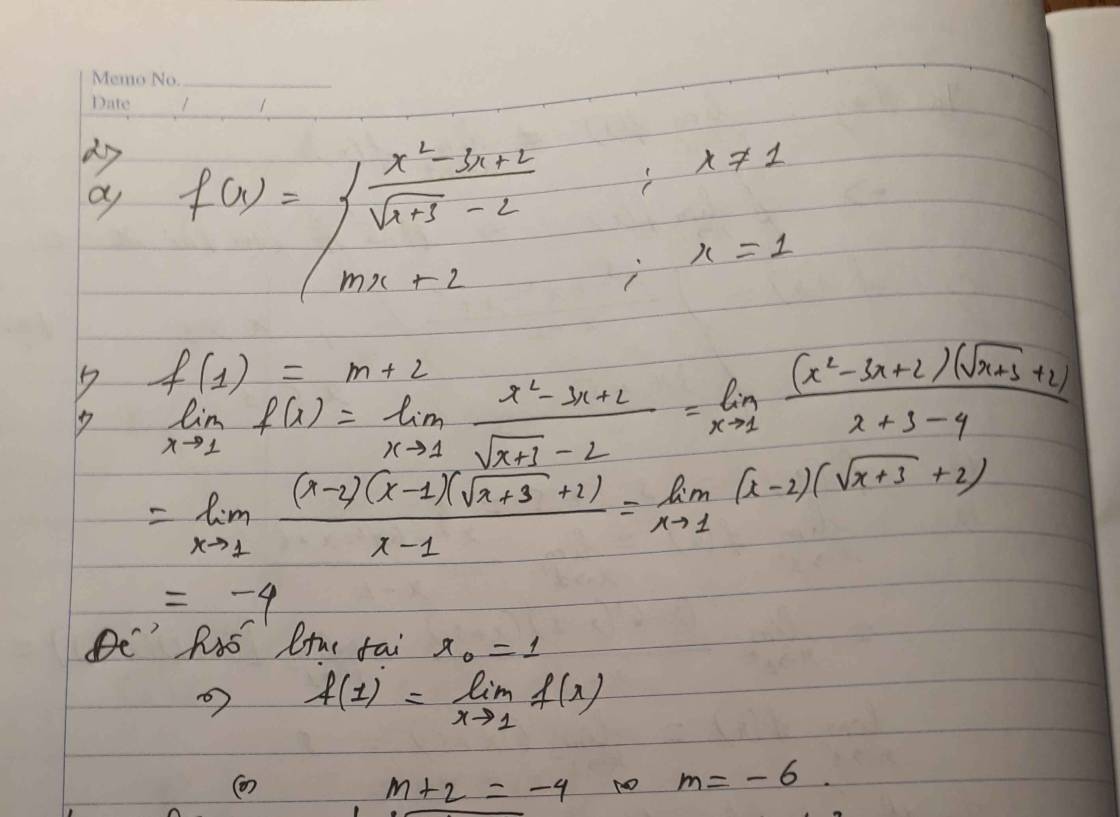\(\left(x^2+1\right).\left(x^3+27\right)=0\)

Những câu hỏi liên quan
\(Bài\) \(2:\) \(Tìm\) \(x:\)
b) \(\left(5-x\right)^3+27=0\)
d) \(\left(x^2-1\right).\left(x+7\right)=0\)
f) \(\left(x^2+81\right).\left(x-7\right).\left(x^2-2\right)=0\)
b) Ta có: \(\left(5-x\right)^3+27=0\)
\(\Leftrightarrow\left(5-x\right)^3=-27\)
\(\Leftrightarrow5-x=-3\)
hay x=8
d) Ta có: \(\left(x^2-1\right)\left(x+7\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+1\right)\left(x+7\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-1\\x=-7\end{matrix}\right.\)
f) Ta có: \(\left(x^2+81\right)\left(x-7\right)\left(x^2-2\right)=0\)
\(\Leftrightarrow\left(x-7\right)\left(x+\sqrt{2}\right)\left(x-\sqrt{2}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=7\\x=\sqrt{2}\\x=-\sqrt{2}\end{matrix}\right.\)
Đúng 1
Bình luận (1)
Tìm x biết :
a ) left(x+3right)left(x^2-3x+9right)-xleft(x-2right)left(x+2right)27
b ) 2x^2+7x+3 0
c ) left(x+3right)left(x^2-3x+9right)-xleft(x-2right)left(x+2right)27
d ) 2x^2+11x+90
e ) xleft(x+2right)-x^2-80
f ) left(x-3right)left(x^2+3x+9right)-xleft(x-2right)left(x+2right)27
Đọc tiếp
Tìm x biết :
a ) \(\left(x+3\right)\left(x^2-3x+9\right)-x\left(x-2\right)\left(x+2\right)=27\)
b ) \(2x^2+7x+3\) = 0
c ) \(\left(x+3\right)\left(x^2-3x+9\right)-x\left(x-2\right)\left(x+2\right)=27\)
d ) \(2x^2+11x+9=0\)
e ) \(x\left(x+2\right)-x^2-8=0\)
f ) \(\left(x-3\right)\left(x^2+3x+9\right)-x\left(x-2\right)\left(x+2\right)=27\)
a) \(\left(x+3\right)\left(x^2-3x+9\right)-x\left(x-2\right)\left(x+2\right)=27\)
\(\Rightarrow x^3+3^3-x\left(x^2-4\right)=27\)
\(\Rightarrow x^3+27-x^3+4x=27\)
\(\Rightarrow27+4x=27\)
\(\Rightarrow4x=0\)
\(\Rightarrow x=0\)
Đúng 0
Bình luận (0)
b) \(2x^2+7x+3=0\)
\(\Rightarrow2x^2+x+6x+3=0\)
\(\Rightarrow x\left(2x+1\right)+3\left(2x+1\right)=0\)
\(\Rightarrow\left(2x+1\right)\left(x+3\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}2x+1=0\\x+3=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}2x=-1\\x=-3\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-\dfrac{1}{2}\\x=-3\end{matrix}\right.\)
Đúng 0
Bình luận (0)
c) Trùng đề bài a
d) \(2x^2+11x+9=0\)
\(\Rightarrow2x^2+2x+9x+9=0\)
\(\Rightarrow2x\left(x+1\right)+9\left(x+1\right)=0\)
\(\Rightarrow\left(x+1\right)\left(2x+9\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x+1=0\\2x+9=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-1\\2x=-9\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-1\\x=-\dfrac{9}{2}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
1/ Xét tính liên tục của hàm số tại một điểm:a) fleft(xright)left{{}begin{matrix}dfrac{x^2-4}{x^2+x-2};xne22x+1;x2end{matrix}right. tại x_02b) fleft(xright)left{{}begin{matrix}left(x+3right)^3-27;x0x^3+27;xle0end{matrix}right. tại x_00c) fleft(xright)left{{}begin{matrix}dfrac{x^3-6x^2-x+6}{x-1};x13x+5;xle1end{matrix}right. tại x_01d) fleft(xright)left{{}begin{matrix}dfrac{sqrt{3x+10}-x-4}{x+2};xne-2-dfrac{1}{4};x-2end{matrix}right. tại x_0-22/ Tìm m để hàm số sau liên tục tại điểm đã chỉ ra:a) ...
Đọc tiếp
1/ Xét tính liên tục của hàm số tại một điểm:
a) \(f\left(x\right)=\left\{{}\begin{matrix}\dfrac{x^2-4}{x^2+x-2};x\ne2\\2x+1;x=2\end{matrix}\right.\) tại \(x_0=2\)
b) \(f\left(x\right)=\left\{{}\begin{matrix}\left(x+3\right)^3-27;x>0\\x^3+27;x\le0\end{matrix}\right.\) tại \(x_0=0\)
c) \(f\left(x\right)=\left\{{}\begin{matrix}\dfrac{x^3-6x^2-x+6}{x-1};x>1\\3x+5;x\le1\end{matrix}\right.\) tại \(x_0=1\)
d) \(f\left(x\right)=\left\{{}\begin{matrix}\dfrac{\sqrt{3x+10}-x-4}{x+2};x\ne-2\\-\dfrac{1}{4};x=-2\end{matrix}\right.\) tại \(x_0=-2\)
2/ Tìm \(m\) để hàm số sau liên tục tại điểm đã chỉ ra:
a) \(f\left(x\right)=\left\{{}\begin{matrix}\dfrac{x^2-3x+2}{\sqrt{x+3}-2};x\ne1\\mx+2;x=1\end{matrix}\right.\) tại \(x_0=1\)
b) \(f\left(x\right)=\left\{{}\begin{matrix}\dfrac{\sqrt[3]{2x^2=9}-3}{2x-6};x\ne3\\m;x=3\end{matrix}\right.\) tại \(x_0=3\)
\(\left(\dfrac{-2}{3}\right)^2.x=\left(\dfrac{-2}{3}\right)^5\)
\(\left(x-\dfrac{1}{2}\right)^3=\dfrac{1}{27}\)
\(\left(\dfrac{2}{3}x-1\right)\left(\dfrac{3}{4}x+\dfrac{1}{2}\right)=0\)
\(\dfrac{4}{9}:x=3\dfrac{1}{3}:2,25\)
\(1\dfrac{1}{3}:0,8=\dfrac{2}{3}:0,1x\)
a: \(x=\left(-\dfrac{2}{3}\right)^5:\left(-\dfrac{2}{3}\right)^2=\left(-\dfrac{2}{3}\right)^3=-\dfrac{8}{27}\)
b: =>x-1/2=1/3
=>x=5/6
c: =>2/3x-1=0 hoặc 3/4x+1/2=0
=>x=3/2 hoặc x=-1/2:3/4=-1/2*4/3=-4/6=-2/3
d =>4/9:x=10/3:9/4=10/3*4/9=40/27
=>x=4/9:40/27=4/9*27/40=108/360=3/10
Đúng 0
Bình luận (0)
Tìm x biết:
\(a.\left(x+1\right)\left(x^2-x+1\right)-x\left(x^2-5\right)=71\)
\(b.\left(2x-3\right)^3-8x\left(x-1\right)^2+4x\left(4x+1\right)+27=0\)
Bài 1:a)left|x-2right|+left|1-dfrac{x}{2}right|0 b)left(x-dfrac{1}{3}right)^3dfrac{-8}{27}c)dfrac{x^2}{6}dfrac{24}{25} c)dfrac{x-1}{x+5}dfrac{6}{7}Giúp mik làm bài này với ạ mik đang cần gấp tối nay mik phải nộp rồi mong mn giúp đỡ mik. Mik cảm ơn mn
Đọc tiếp
Bài 1:
a)\(\left|x-2\right|\)+\(\left|1-\dfrac{x}{2}\right|\)=0 b)\(\left(x-\dfrac{1}{3}\right)^3\)=\(\dfrac{-8}{27}\)
c)\(\dfrac{x^2}{6}\)=\(\dfrac{24}{25}\) c)\(\dfrac{x-1}{x+5}\)=\(\dfrac{6}{7}\)
Giúp mik làm bài này với ạ mik đang cần gấp tối nay mik phải nộp rồi mong mn giúp đỡ mik. Mik cảm ơn mn
Giải pt:
a, \(\dfrac{1}{27}.\left(x-3\right)^2-\dfrac{1}{125}.\left(x-5\right)^3=0\)
b, \(125x^3-\left(2x+1\right)^3-\left(3x-1\right)^3=0\)
c, \(\left(x-3\right)^3+\left(x+1\right)^3=8.\left(x-1\right)^3\)
a: \(\Leftrightarrow\left(\dfrac{1}{3}x-1\right)^3=\left(\dfrac{1}{5}x-1\right)^3\)
=>1/3x-1=1/5x-1
=>2/15x=0
hay x=0
b: Đặt 2x+1=a; 3x-1=b
Theo đề, ta có \(\left(a+b\right)^3-a^3-b^3=0\)
=>3ab(a+b)=0
=>5x(2x+1)(3x-1)=0
hay \(x\in\left\{0;-\dfrac{1}{2};\dfrac{1}{3}\right\}\)
c: Đặt x-3=a; x+1=b
Theo đề, ta có: \(\left(a+b\right)^3=a^3+b^3\)
=>3ab(a+b)=0
=>(x-3)(x+1)(2x-2)=0
hay \(x\in\left\{3;-1;1\right\}\)
Đúng 0
Bình luận (0)
1.Tìm x:
left(x-1right)^3+left(2x+1right)^3+left(x+2right)^33left(x-1right).left(2x+1right).left(x+2right)
2. Cho a+b+c0 . C/m: a^3+b^3+c^33abc
3. Tìm x:
a, left(x+1right)^3+left(2x-3right)^3+left(2-3xright)^30
b, left(2x+1right)^3+left(x+2right)^327left(x+1right)^3
Đọc tiếp
1.Tìm x:
\(\left(x-1\right)^3+\left(2x+1\right)^3+\left(x+2\right)^3=3\left(x-1\right).\left(2x+1\right).\left(x+2\right)\)
2. Cho \(a+b+c=0\) . C/m: \(a^3+b^3+c^3=3abc\)
3. Tìm x:
a, \(\left(x+1\right)^3+\left(2x-3\right)^3+\left(2-3x\right)^3=0\)
b, \(\left(2x+1\right)^3+\left(x+2\right)^3=27\left(x+1\right)^3\)
2. \(a+b+c=0\)
\(\Leftrightarrow\)\(\left(a+b+c\right)^3=0\)
\(\Leftrightarrow a^3+b^3+c^3+3a^2b+3ab^2+3a^{2c}+3ac^2+3b^2c+3bc^2+6abc\)
\(\Leftrightarrow a^3+b^3+c^3+\left(3a^2b+3ab^2+3abc\right)+\left(3a^2c+3ac^2+3abc\right)+\left(3b^2c+3bc^2+3abc\right)-3abc\)
\(\Leftrightarrow a^3+b^3+c^3+3ab\left(a+b+c\right)+3ac\left(a+c+b\right)+3bc\left(b+c+a\right)-3abc\)
Ta có: \(a+b+c=0\)
\(a^3+b^3+c^3+3ab.0+3ac.0+3bc.0=3abc\)
\(\Leftrightarrow a^3+b^3+c^3=3abc\)
Đúng 0
Bình luận (3)
Bài 2
\(a+b+c=0\Rightarrow a=-b-c\)
\(VT=a^3+b^3+c^3=\left(-b-c\right)^3+b^3+c^3\)
\(=\left(-b\right)^3-3\left(-b\right)^2c+3\left(-b\right)c^2-c^3+b^3+c^3\)
\(=\left(-b\right)^3-3b^2c-3bc^2-c^3+b^3+c^3\)
\(=-3b^2c-3bc^2=3bc\left(-b-c\right)=3abc=VP\)
Đúng 0
Bình luận (2)
bài 2
ta có a+b+c=0
=>a+b=-c
=>c=-(a+b)
thay -(a+b)=c vào 2 vế ta đc
a3+b3-(a+b)3=3ab[-a-b)]
=>a3+b3-(a3+3a2b+3ab2+b3)=-3a2b-3ab2
=>a3+b3-a3-3a2b-3ab2-b2=-3ab(a-b)
=>(a3-a3)+(b3-b3)+(-3a2b-3ab2)=-3ab(a-b)
=>0+0-3ab(a-b)=-3ab(a-b)(đpcm)
Đúng 0
Bình luận (6)
Giải phương trìnha. frac{1}{27}cdotleft(x-3right)^3-frac{1}{125}cdotleft(x-5right)^30b.125x^3-left(2x+1right)^3-left(3x-1right)^30c.left(x-3right)^3+left(x+1right)^38cdotleft(x-1right)^3d.left(x^2-3x+2right)cdotleft(x^2+15x+56right)+80e.left(2x^2-3x+1right)cdotleft(2x^2+5x+1right)-9x^20f.left(x+6right)^4+left(x+8right)^4272
Đọc tiếp
Giải phương trình
a. \(\frac{1}{27}\cdot\left(x-3\right)^3-\frac{1}{125}\cdot\left(x-5\right)^3=0\)
b.\(125x^3-\left(2x+1\right)^3-\left(3x-1\right)^3=0\)
c.\(\left(x-3\right)^3+\left(x+1\right)^3=8\cdot\left(x-1\right)^3\)
d.\(\left(x^2-3x+2\right)\cdot\left(x^2+15x+56\right)+8=0\)
e.\(\left(2x^2-3x+1\right)\cdot\left(2x^2+5x+1\right)-9x^2=0\)
f.\(\left(x+6\right)^4+\left(x+8\right)^4=272\)
Tìm x
a, \(9x^2-49=0\) b, \(\left(x+3\right)\left(x^2-3x+9\right)-x\left(x-1\right)-27=0\)
c, (x-1)(x+2)-x-2=0 d, \(x\left(3x+2\right)+\left(x+1\right)^2-\left(2x-5\right)\left(2x+5\right)=0\)
e, (4x+1)(x-2)-(2x-3)(2x+1)=7