Cho 3 điểm A,B,C có tọa độ là A(-1,-2) B(3,2) C(4,-1) Tìm O để tam giác OAB đều

Những câu hỏi liên quan
Trong mặt phẳng tọa độ Oxy, cho tam giác OAB với A(1; 3) và B (4; 2). Tìm tọa độ điểm E là chân đường phân giác trong góc O của tam giác OAB A.
E
5
2
;
5
2
.
B.
E
3
2
;
−...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho tam giác OAB với A(1; 3) và B (4; 2). Tìm tọa độ điểm E là chân đường phân giác trong góc O của tam giác OAB
A. E = 5 2 ; 5 2 .
B. E = 3 2 ; − 1 2 .
C. E = − 2 + 3 2 ; 4 + 2 .
D. E = − 2 + 3 2 ; 4 − 2 .
Theo tính chất đường phân giác của tam giác ta có E A E B = O A O B = 2 2 .
Vì E nằm giữa hai điểm A, B nên E A → = − 2 2 E B → . *
Gọi E(x; y). Ta có E A → = 1 − x ; 3 − y E B → = 4 − x ; 2 − y .
Từ (*), suy ra 1 − x = − 2 2 4 − x 3 − y = − 2 2 2 − y ⇔ x = − 2 + 3 2 y = 4 − 2 .
Chọn D.
Đúng 0
Bình luận (0)
Câu 1: Cho tam giác ABC có A(3,2); B(4,1) và C(1,5).a/ Tìm tọa độ trọng tâm G của tam giác ABC.b/ Tìm tọa độ điểm D để ABCD là hình bình hànhc/ Tìm tọa độ sao cho Câu 2: Cho ngũ giác ABCDE. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DE. I, J là trung điểm của MP, NQ. Chứng minh rằng:
Đọc tiếp
Câu 1: Cho tam giác ABC có A(3,2); B(4,1) và C(1,5).
a/ Tìm tọa độ trọng tâm G của tam giác ABC.
b/ Tìm tọa độ điểm D để ABCD là hình bình hành
c/ Tìm tọa độ ![]() sao cho
sao cho ![]()
Câu 2: Cho ngũ giác ABCDE. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DE. I, J là trung điểm của MP, NQ. Chứng minh rằng: 
1.
a, Trọng Tâm G: \(\left\{{}\begin{matrix}x_G=\dfrac{x_A+x_B+x_C}{3}=\dfrac{8}{3}\\y_G=\dfrac{y_A+y_B+y_C}{3}=\dfrac{8}{3}\end{matrix}\right.\)
\(\Rightarrow G=\left(\dfrac{8}{3};\dfrac{8}{3}\right)\)
b, \(ABCD\) là hình bình hành \(\Leftrightarrow\vec{AB}=\vec{DC}\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_B-x_A=x_C-x_D\\y_B-y_A=y_C-y_D\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_D=0\\y_D=6\end{matrix}\right.\)
\(\Rightarrow D=\left(0;6\right)\)
c, \(\vec{AM}=3\vec{BC}\Leftrightarrow\left\{{}\begin{matrix}x_M=x_A+3\left(x_C-x_B\right)=-6\\y_M=y_A+3\left(y_C-y_B\right)=14\end{matrix}\right.\)
\(\Rightarrow M=\left(-6;14\right)\)
Đúng 1
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, cho các điểm A(1; 3), B(2; 4), C(-3; 2).
a) Chứng minh rằng A, B, C là ba đỉnh của một tam giác.
b) Tìm tọa độ trung điểm M của đoạn thẳng AB.
c) Tìm tọa độ trọng tâm G của tam giác ABC.
d) Tìm điểm D(x; y) để O(0; 0) là trọng tâm của tam giác ABD.
a)
Ta có: \(\overrightarrow {AB} = \left( {2 - 1;4 - 3} \right) = \left( {1;1} \right),\;\overrightarrow {AC} = \left( { - 3 - 1;2 - 3} \right) = \left( { - 4; - 1} \right)\)
Hai vectơ này không cùng phương (vì \(\frac{1}{{ - 4}} \ne \frac{1}{{ - 1}}\)).
Do đó các điểm A, B, C không cùng nằm trên một đường thẳng.
Vậy A, B, C là ba đỉnh của một tam giác.
b) Trung điểm M của đoạn thẳng AB có tọa độ là \(\left( {\frac{{1 + 2}}{2};\frac{{3 + 4}}{2}} \right) = \left( {\frac{3}{2};\frac{7}{2}} \right)\)
c) Trọng tâm G của tam giác ABC có tọa độ là \(\left( {\frac{{1 + 2 + \left( { - 3} \right)}}{3};\frac{{3 + 4 + 2}}{3}} \right) = \left( {0;3} \right)\)
d) Để O(0; 0) là trọng tâm của tam giác ABD thì \(\left( {0;0} \right) = \left( {\frac{{{x_A} + {x_B} + {x_D}}}{3};\frac{{{y_A} + {y_B} + {y_D}}}{3}} \right)\)
\( \Leftrightarrow \left( {0;0} \right) = \left( {\frac{{1 + 2 + x}}{3};\frac{{3 + 4 + y}}{3}} \right)\)
\(\begin{array}{l} \Leftrightarrow \left( {0;0} \right) = \left( {1 + 2 + x;3 + 4 + y} \right)\\ \Leftrightarrow \left( {0;0} \right) = \left( {x + 3;y + 7} \right)\\ \Leftrightarrow \left\{ \begin{array}{l}0 = x + 3\\0 = y + 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - 3\\y = - 7\end{array} \right.\end{array}\)
Vậy tọa độ điểm D là (-3; -7).
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, xét đường thẳng (d): y = mx + 4 với m≠0.
1. Gọi A là giao điểm của đường thẳng (d) và trục Oy. TÌm tọa độ điểm A.
2. Tìm tất cả các giá trị của m để đường thẳng (d) cắt trục Ox tại điểm B sao cho tam giác OAB là tam giác cân.
Cho hàm số \(y=\frac{3x+4}{3x+3}\) có đồ thị (C). Tìm các giá trị tham số m để đường thẳng d : y = x + m cắt đồ thị (C) tại hai điểm phân biệt A và B sao cho tam giác OAB đều ( với O là gốc tọa độ)
Phương trình hoành độ giao điểm \(3x^2+2mx+3m-4=0\left(1\right)\) với x. Đường thẳng d cắt đồ thị (C) tại hai điểm phân biệt khi và chỉ khi phương trình (1) có 2 nghiệm phân biệt khác -1
\(\Leftrightarrow\begin{cases}9m^2-36m+48>0\\0.m-1\ne0\end{cases}\) (đúng với mọi m)
Gọi \(x_1;x_2\) là các nghiệm của phương trình (1), ta có : \(\begin{cases}x_1+x_2=-m\\x_1x_2=\frac{3m-4}{3}\end{cases}\) (*)
Giả sử \(A\left(x_1;x_1+m\right);B\left(x_2;x_2+m\right)\)
Khi đó ta có \(OA=\sqrt{x^2_1+\left(x_1+m\right)^2};OA=\sqrt{x^2_2+\left(x_2+m\right)^2}\)
Kết hợp (*) ta được \(OA=OB=\sqrt{x_1^2+x_2^2}\)
Suy ra tam giác OAB cân tại O
Ta có \(AB=\sqrt{2\left(x_1-x_2\right)^2}\). Tam giác OAB đều \(\Leftrightarrow OA^2=AB^2\Leftrightarrow x_1^2+x_2^2=2\left(x_1-x_2\right)^2\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-6x_1x_2=0\)
\(\Leftrightarrow m^2-6m+8=0\Leftrightarrow m=2\) hoặc m=4
Đúng 0
Bình luận (0)
a) Vẽ đồ thị các hàm số sau trên cùng một mặt phẳng tọa độ:y 2x (1); y 0,5x (2); y -x + 6 (3)b) Gọi các giao điểm của đường thẳng có phương trình (3) với hai đường thẳng có phương trình (1) và (2) theo thứ tự là A và B. Tìm tọa độ của hai điểm A và B.c) Tính các góc của tam giác OAB.Hướng dẫn câu c)Tính OA, OB rồi chứng tỏ tam giác OAB là tam giác cân.
T
í
n
h
AOB
^
,
AOx
^...
Đọc tiếp
a) Vẽ đồ thị các hàm số sau trên cùng một mặt phẳng tọa độ:
y = 2x (1); y = 0,5x (2); y = -x + 6 (3)
b) Gọi các giao điểm của đường thẳng có phương trình (3) với hai đường thẳng có phương trình (1) và (2) theo thứ tự là A và B. Tìm tọa độ của hai điểm A và B.
c) Tính các góc của tam giác OAB.
Hướng dẫn câu c)
Tính OA, OB rồi chứng tỏ tam giác OAB là tam giác cân.
T í n h AOB ^ , AOx ^ − BOx ^
a) – Vẽ đồ thị y = 2x (1):
Cho x= 0 ⇒ y= 0 ta được O (0, 0)
Cho x= 2 ⇒ y = 4 ta được điểm (2; 4)
- Vẽ đồ thị y = 0,5x (2):
Cho x= 0 ⇒ y = 0 ta được O (0; 0)
Cho x = 4 ⇒ y = 2 ta được điểm (4; 2)
- Vẽ đồ thị y = -x + 6 (3):
Cho x = 0 ⇒ y = 6 được điểm (0; 6)
Cho y = 0 ⇒ x = 6 được điểm (6; 0)
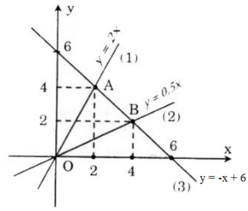
b) Theo đề bài A, B theo thứ tự là giao điểm của đường thẳng (3) với các đường thẳng (1) và (2), nên ta có:
Hoành độ giao điểm của A là nghiệm của phương trình:
- x + 6 = 2x ⇒ x = 2
=> y = 4 => A(2; 4)
Hoành độ giao điểm của B là nghiệm của phương trình:
- x + 6 = 0,5x ⇒ x = 4
⇒ y = 2 ⇒ B(4; 2)
c) Ta có:

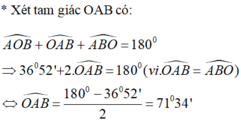
Đúng 0
Bình luận (0)
Trên mặt phẳng Oxy, cho hai điểm A(1; 3), B(4; 2).
a) Tìm tọa độ điểm D nằm trên trục Ox sao cho DA = DB;
b) Tính chu vi tam giác OAB.
c) Chứng tỏ OA vuông góc với AB và từ đó tính diện tích tam giác OAB.
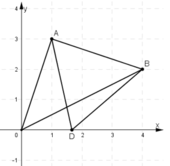
a) D nằm trên trục Ox nên D có tọa độ D(x ; 0)
Khi đó :
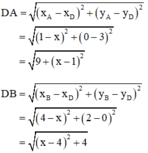
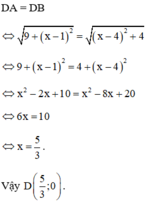
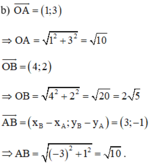
Vậy chu vi tam giác OAB là P = AO + BO + AB = √10 + 2√5 + √10 = 2√5 + 2√10
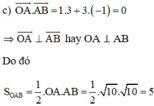
Đúng 0
Bình luận (0)
Cho ba điểm A (0,6) B(-3,2) C(5,-1)
A ) chứng minh rằng A , B ,C lập thành một tam giác
B ) Tìm tọa độ điểm M ,N , P lần lượt là trung điểm của AB , BC và CA
C ) Tìm tọa độ điểm D sao cho A là trọng tâm tam giác BCD
D ) Tìm tọa độ điểm E sao cho tứ giác ABEC là hình bình hành
Câu 1: Cho tam giác ABC có A(3,2); B(4,1) và C(1,5).
a/ tìm tọa độ u vecto 3ab vecto + 2bc vecto
b/ Tìm tọa độ điểm D để ABCD là hình bình hành
mai em thi rồi giúp em với ạ
Đọc tiếp
\(\left\{{}\begin{matrix}\overrightarrow{AB}=\left(1;-1\right)\\\overrightarrow{BC}=\left(-3;4\right)\end{matrix}\right.\)
\(\Rightarrow\overrightarrow{u}=3\overrightarrow{AB}+2\overrightarrow{BC}=\left(-3;5\right)\)
Gọi \(D\left(x;y\right)\Rightarrow\overrightarrow{DC}=\left(1-x;5-y\right)\)
Để ABCD là hbh \(\Leftrightarrow\overrightarrow{AB}=\overrightarrow{DC}\)
\(\Leftrightarrow\left\{{}\begin{matrix}1-x=1\\5-y=-1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=0\\y=6\end{matrix}\right.\)
\(\Rightarrow D\left(0;6\right)\)
Đúng 1
Bình luận (0)














