Các câu hỏi tương tự
Bài 1: Cho hàm số yx2 có đồ thị (P) và hàm số y4x+m có đồ thị (dm) Tìm tất cả các giá trị của m sao cho (dm) và (P) cắt nhau tại hai điểm phân biệt, trong đó trung độ của một trong hai giao điểm đó bằng 1 Bài 2: Trong mặt phẳng Oxy cho parapol (P): yx2 Trên (P) lấy điểm A có hoành độ xA -2. Tìm tọa độ điểm M trên trục Ox sao cho |MA-MB| đạt giá trị lớn nhất, biết B(1;1) Bài 3: Tìm a và b để đường thẳng (d): y(a-2)x+b có hệ số góc bằng 4 và đi qua điểm M(1;-3) Bài 4:Cho hàm số y2x-5 có đồ thị là...
Đọc tiếp
Bài 1: Cho hàm số y=x2 có đồ thị (P) và hàm số y=4x+m có đồ thị (dm) Tìm tất cả các giá trị của m sao cho (dm) và (P) cắt nhau tại hai điểm phân biệt, trong đó trung độ của một trong hai giao điểm đó bằng 1 Bài 2: Trong mặt phẳng Oxy cho parapol (P): y=x2 Trên (P) lấy điểm A có hoành độ xA =-2. Tìm tọa độ điểm M trên trục Ox sao cho |MA-MB| đạt giá trị lớn nhất, biết B(1;1) Bài 3: Tìm a và b để đường thẳng (d): y=(a-2)x+b có hệ số góc bằng 4 và đi qua điểm M(1;-3) Bài 4:Cho hàm số y=2x-5 có đồ thị là đường thẳng (d) a.Gọi A,B lần lượt là giao điểm của (d) với các trục tọa độ Ox,Oy. Tính tọa độ các điểm A,B và vẽ đường thẳng (d) trong mặt phẳng tọa độ Oxy b.Tính diện tích tam giác AOB HELP!!
Bài 1: Cho hàm số yx2 có đồ thị (P) và hàm số y4x+m có đồ thị (dm) Tìm tất cả các giá trị của m sao cho (dm) và (P) cắt nhau tại hai điểm phân biệt, trong đó trung độ của một trong hai giao điểm đó bằng 1 Bài 2: Trong mặt phẳng Oxy cho parapol (P): yx2 Trên (P) lấy điểm A có hoành độ xA -2. Tìm tọa độ điểm M trên trục Ox sao cho |MA-MB| đạt giá trị lớn nhất, biết B(1;1) Bài 3: Tìm a và b để đường thẳng (d): y(a-2)x+b có hệ số góc bằng 4 và đi qua điểm M(1;-3) Bài 4:Cho hàm số y2x-5 có đồ thị là...
Đọc tiếp
Bài 1: Cho hàm số y=x2 có đồ thị (P) và hàm số y=4x+m có đồ thị (dm) Tìm tất cả các giá trị của m sao cho (dm) và (P) cắt nhau tại hai điểm phân biệt, trong đó trung độ của một trong hai giao điểm đó bằng 1 Bài 2: Trong mặt phẳng Oxy cho parapol (P): y=x2 Trên (P) lấy điểm A có hoành độ xA =-2. Tìm tọa độ điểm M trên trục Ox sao cho |MA-MB| đạt giá trị lớn nhất, biết B(1;1) Bài 3: Tìm a và b để đường thẳng (d): y=(a-2)x+b có hệ số góc bằng 4 và đi qua điểm M(1;-3) Bài 4:Cho hàm số y=2x-5 có đồ thị là đường thẳng (d) a.Gọi A,B lần lượt là giao điểm của (d) với các trục tọa độ Ox,Oy. Tính tọa độ các điểm A,B và vẽ đường thẳng (d) trong mặt phẳng tọa độ Oxy b.Tính diện tích tam giác AOB HELP!!
Trong mặt phẳng tọa độ Oxy cho các đường thẳng (d) : y=mx−2m−1, m là số thực
1. Chứng minh với mọi số thực m thì các đường thẳng (d) luôn đi qua một điểm cố định
2. Gọi A và B lần lượt là giao điểm của (d) với trục Ox và trục Oy. Tìm m để diện tích tam giác OAB bằng 2
Trong mặt phẳng tọa độ Oxy, cho đường thẳng (d): y = (2m-7n)x +3m+5n đi qua điểm M (1; 1) và cắt hai trục Ox, Oy lần lượt tại A, B sao cho tam giác OAB cân. Gọi C, D lần lượt là các điểm đối xứng của A và B qua O. Tính chu vi và diện tích của tứ giác ABCD.
trong mặt phẳng tọa độ Oxy cho điểm A(-2; 2) và đường thẳng (d): y -2x - 2a. chứng minh A thuộc (d)b. tìm các giá trị của a để Parapol: y ax2 đi qua Ac. tìm đường thẳng đi qua A và vuông góc với đường thẳng (d)d. gọi A và B là giao điểm của (P) với đường thẳng tìm được trong câu c, và C là giao điểm của đường thẳng (d) với trục Oy. tìm tọa độ các điểm B, C và tính diện tích tam giác ABC
Đọc tiếp
trong mặt phẳng tọa độ Oxy cho điểm A(-2; 2) và đường thẳng (d): y = -2x - 2
a. chứng minh A thuộc (d)
b. tìm các giá trị của a để Parapol: y = ax2 đi qua A
c. tìm đường thẳng đi qua A và vuông góc với đường thẳng (d)
d. gọi A và B là giao điểm của (P) với đường thẳng tìm được trong câu c, và C là giao điểm của đường thẳng (d) với trục Oy. tìm tọa độ các điểm B, C và tính diện tích tam giác ABC
Trong mặt phẳng tọa độ Oxy cho các đường thẳng (d) : \(y=mx-2m-1\) , m là số thực
1. Chứng minh với mọi số thực m thì các đường thẳng (d) luôn đi qua một điểm cố định
2. Gọi A và B lần lượt là giao điểm của (d) với trục Ox và trục Oy. Tìm m để diện tích tam giác OAB bằng 2
cho hàm số y(m+3)x+2 (d) . tìm m đểa, đường thẳng (d) cắt Ox và Oy lần lượt tại A và Bsao cho tam giác OAB cânb, diện tích tam giác OAB bằng 1c, khoảng cách từ gốc tọa độ đến đường thẳng (d) đạt giá trị lớn nhấtd, khoảng cách từ gốc tọa độ đến đường thẳng (d) bằng 2e, đường thẳng (d) cắt trục Ox tại điểm có hoành độ bằng 2f, đường thẳng (d) cắt trục Ox tại điểm có hoành độ lớn hơn 2
Đọc tiếp
cho hàm số y=(m+3)x+2 (d) . tìm m để
a, đường thẳng (d) cắt Ox và Oy lần lượt tại A và Bsao cho tam giác OAB cân
b, diện tích tam giác OAB bằng 1
c, khoảng cách từ gốc tọa độ đến đường thẳng (d) đạt giá trị lớn nhất
d, khoảng cách từ gốc tọa độ đến đường thẳng (d) bằng 2
e, đường thẳng (d) cắt trục Ox tại điểm có hoành độ bằng 2
f, đường thẳng (d) cắt trục Ox tại điểm có hoành độ lớn hơn 2
Trong mặt phẳng tọa độ Oxy cho đường thẳng (d) : y = ( k - 1 )x + n và hai điểm A(0;2),B(-1;0)
cho n = 2 . Tìm k để đường thẳng (d) cắt trục ox tại điểm C sao cho diện tích tam giác OAC gấp 2 lần diện tích tam giác OABa) Vẽ đồ thị của các hàm số y x và y 2x trên cùng một mặt phẳng tọa độ Oxy (hình 5).b) Đường thẳng song song với trục Ox và cắt trục Oy tại các điểm có tung độ y 4 lần lượt cắt các đường thẳng y 2x, y x tại hai điểm A và B.Tìm tọa độ các điểm A, B, tính chu vi, diện tích của tam giác OAB theo đơn vị đo trên các trục tọa độ là xentimetHình 5
Đọc tiếp
a) Vẽ đồ thị của các hàm số y = x và y = 2x trên cùng một mặt phẳng tọa độ Oxy (hình 5).
b) Đường thẳng song song với trục Ox và cắt trục Oy tại các điểm có tung độ y = 4 lần lượt cắt các đường thẳng y = 2x, y = x tại hai điểm A và B.
Tìm tọa độ các điểm A, B, tính chu vi, diện tích của tam giác OAB theo đơn vị đo trên các trục tọa độ là xentimet
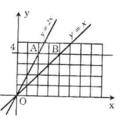
Hình 5









