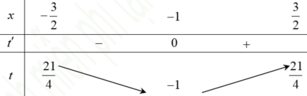
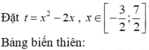phương trình2sin5x/2 .sinx/2 -mcosx +1=0 có đúng 7 nghiệm thuộc(-pi/2;2pi). tìm cá giá trị của m

Những câu hỏi liên quan
cho phương trình cos3x-cos2x+mcosx-1=0
tìm m để phương trình có 7 nghiệm thuộc \(\left(\frac{-\pi}{2};\frac{\pi}{2}\right)\)
\(\Leftrightarrow4cos^3x-3cosx-\left(2cos^2x-1\right)+m.cosx-1=0\)
\(\Leftrightarrow4cos^3x-2cos^2x+\left(m-3\right)cosx=0\)
\(\Leftrightarrow cosx\left(4cos^2x-2cosx+m-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=0\left(1\right)\\4cos^2x-2cosx+m-3=0\left(2\right)\end{matrix}\right.\)
Xét (1) \(\Rightarrow x=\frac{\pi}{2}+k\pi\) không có nghiệm nào trên khoảng đã cho
\(\Rightarrow\) (2) phải có 7 nghiệm trên khoảng đã cho
Mà (2) là pt bậc 2 nên có tối đa 2 nghiệm cosx, ứng với mỗi giá trị cosx cũng có tối đa 2 nghiệm x thuộc khoảng đã cho
\(\Rightarrow\) (2) có tối đa 4 nghiệm
Không tồn tại m thỏa mãn yêu cầu
Đúng 0
Bình luận (0)
Cho hàm số y f(x) có đồ thị như hình vẽ bên. Tìm số giá trị nguyên của m để phương trình
f
(
x
2
-
2
x
)
m
có đúng 4 nghiệm thực phân biệt thuộc đoạn
[
-
3
2...
Đọc tiếp
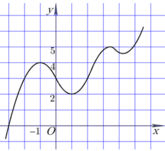
Cho hàm số y = f(x) có đồ thị như hình vẽ bên. Tìm số giá trị nguyên của m để phương trình
f
(
x
2
-
2
x
)
=
m
có đúng 4 nghiệm thực phân biệt thuộc đoạn
[
-
3
2
;
7
2
]
.
A. 1
B. 4
C. 2
D. 3
Cho ba số a,b,c khác 0 thỏa mãn a/7 + b/5 + c/3 =0
Chứng minh rằng phương trình ax4 +bx2 + c = 0 có ít nhất 1 nghiệm thuộc (0;1)
giả sử pt \(ax^2+bx+c=0\left(a,b,c\ne0\right)\) có 2 nghiệm phân biệt trong đó có đúng 1 nghiệm dương x1 thì phương trình bậc hai \(ct^2+bt+a=0\) cũng có hai nghiệm phân biệt trong đó có \(t_1>0\) thoả mãn \(x_1+t_1\ge2\)
CÁI BÀI NÀY CÂU HỎI LÀ LÀM GÌ VẬY ĐỌC KO HỈU LẮM
Đúng 0
Bình luận (0)
phantuananh mk cũng bị cái câu hỏi làm cho @@ ùi
Đúng 0
Bình luận (0)
x1 là nghiệm pt
=> \(ax1^2+bx1+c=0\)
<=> \(a+b\cdot\frac{1}{x1}+c\cdot\left(\frac{1}{x1}\right)^2=0\Leftrightarrow ct1^2+bt1+a=0\) ( t1 = 1/x1)
Xet \(x1+t1=x1+\frac{1}{x1}\ge2\) ( BĐT cô - si , x1 > 0 )
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Tìm các giá trị của m để phương trình sau có đúng 2 nghiệm phân biệt :
\(x^3-m\left(x+1\right)+1=0\).
1) tìm m để phương trình 2sinx+mcosx1-m có nghiệm x thuộc left[-frac{pi}{2};frac{pi}{2}right]
2) tìm nghiệm của phương trình : sinx^24x+3.sin4x.cos4x-4.cos^24x0 khoảng left(0;frac{pi}{2}right)
3) tìm tất cả các nghiệm của phương trình cos5x.cosx cos4x.cos2x+ 3cos^2x+1 thuộc khoảng left(-pi;piright)
4) tìm tất cả các nghiệm trong khoảng (frac{2pi}{5};frac{6pi}{7}) của phương trình: sqrt{3}sin7x-cos7xsqrt{2}
Đọc tiếp
1) tìm m để phương trình 2sinx+mcosx=1-m có nghiệm x thuộc \(\left[-\frac{\pi}{2};\frac{\pi}{2}\right]\)
2) tìm nghiệm của phương trình : \(sinx^24x+3.sin4x.cos4x-4.cos^24x=0\) khoảng \(\left(0;\frac{\pi}{2}\right)\)
3) tìm tất cả các nghiệm của phương trình cos5x.cosx= cos4x.cos2x+ \(3cos^2x+1\) thuộc khoảng \(\left(-\pi;\pi\right)\)
4) tìm tất cả các nghiệm trong khoảng (\(\frac{2\pi}{5};\frac{6\pi}{7}\)) của phương trình: \(\sqrt{3}sin7x-cos7x=\sqrt{2}\)
Trong [0;π], phương trình sinx = 1-cos2x có tập nghiệm là gì ?
\(\Leftrightarrow sinx=sin^2x\Leftrightarrow\left[{}\begin{matrix}sinx=0\\sinx=1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k\pi\\x=\frac{\pi}{2}+k2\pi\end{matrix}\right.\) \(\Rightarrow x=\left\{0;\pi;\frac{\pi}{2}\right\}\)
cho phương trình \(cos^2\left(x\right)\) +mcosx-m+1=0. Tìm m để phương trình
a, Vô nghiệm trong khoảng(\(\frac{\pi}{2}\) , \(\frac{3\pi}{2}\) )
b,có 7 nghiệm thuộc khoảng (0, 5π)
Câu 1 :Chứng minh phương trình 11x^2+5=y^2 có vô số nghiệm nguyên có dạng y=11z-4; z thuộc Z
Câu 2 : Chưng minh phương trình: 7x^2+2= y^2 có vô số nghiệm nguyên.
Câu 3 : Tìm các số nguyên thoả mãn: 8x^2y^2 +x^2+y^2=10xy
MÌNH ĐANG CẦN GẤP GIẢI GIÚP MÌNH NHA !