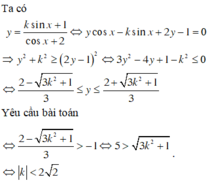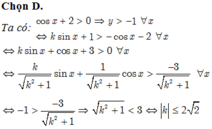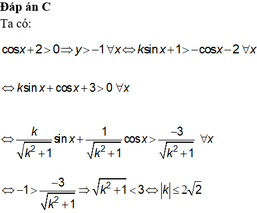Tìm k để giá trị nhỏ nhất của hàm số y=\(\frac{ksinx+1}{cosx+2}\)lớn hơn -1

Những câu hỏi liên quan
Cho hàm số y = \(\frac{ksinx+1}{cosx+2}\) . Tìm k để giá trị nhỏ nhất của hàm số nhỏ hơn -1
Lời giải:
Ta có:
\(y=\frac{k\sin x+1}{\cos x+2}\Rightarrow y\cos x+2y=k\sin x+1\)
\(\Leftrightarrow 2y-1=k\sin x-y\cos x\)
Theo BĐT Bunhiacopxky:
\((2y-1)^2=(k\sin x-y\cos x)^2\leq (k^2+y^2)(\sin ^2x+\cos ^2x)=k^2+y^2\)
\(\Leftrightarrow 4y^2-4y+1\leq k^2+y^2\)
\(\Leftrightarrow 3y^2-4y+1\leq k^2\)
\(\Leftrightarrow 3(y-\frac{2}{3})^2\leq k^2+\frac{1}{3}\)
\(\Leftrightarrow \frac{2}{3}-\sqrt{\frac{3k^2+1}{9}}\leq y\leq \frac{2}{3}+\sqrt{\frac{3k^2+1}{9}}\)
\(\Rightarrow y_{\min}=\frac{2}{3}-\sqrt{\frac{3k^2+1}{9}}\)
Để \(y_{\min}< -1\Leftrightarrow \sqrt{\frac{3k^2+1}{9}}>\frac{5}{3}\Leftrightarrow k^2>8\Leftrightarrow \left[\begin{matrix} k>2\sqrt{2}\\ k<-2\sqrt{2}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Tìm k để giá trị nhỏ nhất của hàm số
y
ksinx
+
1
cosx
+
2
lớn hơn -1. A.
k
2
B.
k
2
3
C. ...
Đọc tiếp
Tìm k để giá trị nhỏ nhất của hàm số y = ksinx + 1 cosx + 2 lớn hơn -1.
A. k < 2
B. k < 2 3
C. k < 3
D. k < 2 2
Tìm k để giá trị nhỏ nhất của hàm số y f(x)
k
sin
x
+
1
cos
x
+
2
lớn hơn -1? A.
k
2
B.
k
2
3
C. ...
Đọc tiếp
Tìm k để giá trị nhỏ nhất của hàm số
y = f(x) = k sin x + 1 cos x + 2 lớn hơn -1?
A. k < 2
B. k < 2 3
C. k < 3
D. k < 2 2
Chọn D
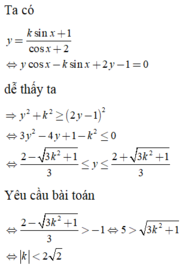
· Bổ trợ kiến thức: Để cho bài toán được dễ hiểu hơn các em có thể nghĩ hướng giải một cách đơn giản như sau, đầu tiên là các em dùng kiến thức về min, max của hàm số để tìm các GTLN và GTNN của hàm số ( kể cả có tham số hay không có tham số ), sau đó giải quyết min > –1 vậy là hoàn thành xong bài toán.
Bước khó khăn của bài toán trên là bước tìm min của 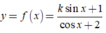
do gặp phải tham số k nhưng nếu dùng các kĩ thuật sơ cấp để xử lí và dễ tìm thấy được 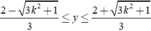 ,
,
khi đó ta chỉ cần tìm k sao cho min y > –1 vậy là ta chọn được đáp án đúng.
Đúng 0
Bình luận (0)
Tìm k để giá trị nhỏ nhất của hàm số
y
k
sin
x
+
1
cos
x
+
2
lớn hơn A.
k
2
B.
k
2
3
C. ...
Đọc tiếp
Tìm k để giá trị nhỏ nhất của hàm số y = k sin x + 1 cos x + 2 lớn hơn
A. k < 2
B. k < 2 3
C. k < 3
D. k < 2 2
Tìm k để GTNN của hàm số
y
k
sin
x
+
1
cos
x
+
2
lớn hơn -1?
Đọc tiếp
Tìm k để GTNN của hàm số y = k sin x + 1 cos x + 2 lớn hơn -1?
![]()
![]()
![]()
![]()
Tìm k để GTNN của hàm số
y
k
sin
x
+
1
cos
x
+
2
lớn hơn -1? A.
|
k
|
≤
2
B.
|
k
|
≤
2
3
C. ...
Đọc tiếp
Tìm k để GTNN của hàm số y = k sin x + 1 cos x + 2 lớn hơn -1?
A. | k | ≤ 2
B. | k | ≤ 2 3
C. | k | ≤ 2 2
D. | k | ≤ 3
1/ tìm TXĐ chủa hàm số y = căn 1 - cosx /2 + sinx.
2/ tìm tập giá trị của hàm số y = 2-cos2x.
3/ Tìm giá trị lớn nhất và nhỏ nhất của các hàm số sau :
a) y=1 + 2sinx b)y=1 - 2cos^2x
4/ Tìm giá trị nhỏ nhất của hàm số y=tan^2x - 2tanx +3.
1. Không dịch được đề
2.
\(-1\le cos2x\le1\Rightarrow1\le y\le3\)
3.
a. \(-2\le2sinx\le2\Rightarrow-1\le y\le3\)
\(y_{min}=-1\) khi \(sinx=-1\Rightarrow x=-\dfrac{\pi}{2}+k2\pi\)
\(y_{max}=3\) khi \(sinx=1\Rightarrow x=\dfrac{\pi}{2}+k2\pi\)
b.
\(0\le cos^2x\le1\Rightarrow-1\le y\le2\)
\(y_{min}=-1\) khi \(cos^2x=1\Rightarrow x=k\pi\)
\(y_{max}=2\) khi \(cosx=0\Rightarrow x=\dfrac{\pi}{2}+k\pi\)
4.
\(y=\left(tanx-1\right)^2+2\ge2\)
\(y_{min}=2\) khi \(tanx=1\Rightarrow x=\dfrac{\pi}{4}+k\pi\)
Đúng 0
Bình luận (0)
tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số
\(y=\dfrac{sinx+3cosx+1}{sinx-cosx+2}\)
\(ĐK:sinx-cosx\ne-2\)
\(< =>2y-1=sinx\left(1-y\right)+cosx\left(y+3\right)\)
Theo Bunhiacopxki:
\(\left[sinx\left(1-y\right)+cosx\left(y+3\right)\right]^2\)\(\le\left(sin^2x+cos^2x\right)\left[\left(1-y\right)^2+\left(y+3\right)^2\right]\)
\(< =>\left(2y-1\right)^2\le2y^2+4y+10\)
\(< =>2y^2-8y-9\le0\)
=> Bấm máy tìm Max, Min của y
(Sry máy tính của t bị ngáo không bấm ra)
Đúng 2
Bình luận (0)
\(\Rightarrow y.sinx-y.cosx+2y=sinx+3cosx+1\)
\(\Rightarrow\left(y-1\right)sinx-\left(y+3\right)cosx=1-2y\)
Theo điều kiện có nghiệm của pt lượng giác bậc nhất
\(\Rightarrow\left(y-1\right)^2+\left(y+3\right)^2\ge\left(1-2y\right)^2\)
\(\Leftrightarrow2y^2-8y-9\le0\)
\(\Rightarrow\dfrac{4-\sqrt{34}}{2}\le y\le\dfrac{4+\sqrt{34}}{2}\)
\(y_{max}=\dfrac{4+\sqrt{34}}{2}\) ; \(y_{min}=\dfrac{4-\sqrt{34}}{2}\)
Đúng 1
Bình luận (0)
\(y=\dfrac{sinx+3cosx+1}{sinx-cosx+2}\)
\(\Leftrightarrow y.sinx-y.cosx+2y=sinx+3cosx+1\)
\(\Leftrightarrow\left(y-1\right)sinx-\left(y+3\right).cosx=1-2y\)
Phương trình có nghiệm khi \(\left(y-1\right)^2+\left(y+3\right)^2\ge\left(1-2y\right)^2\)
\(\Leftrightarrow y^2-2y+1+y^2+6y+9\ge4y^2-4y+1\)
\(\Leftrightarrow2y^2-8y-9\le0\)
\(\Leftrightarrow\dfrac{4-\sqrt{34}}{2}\le y\le\dfrac{4+\sqrt{34}}{2}\)
Đúng 1
Bình luận (0)
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số sau:
y=sinx - cosx -sin2x + 1
y=2( sinx + cosx )+4 sinx.cosx - 2