Mọi người ơi giúp mik với ai làm đc mik tick cho, làm đc hả nào thì mik tick cho nha

Những câu hỏi liên quan
Mọi người ơi giúp mik với ai làm đc mik tick , làm đc câu nào mik tick cho
a, Áp dụng t/c dtsbn:
\(\dfrac{a}{b}=\dfrac{c}{d}=\dfrac{a+c}{b+d}\)
b, Áp dụng t/c dtsbn:
\(\dfrac{a}{b}=\dfrac{c}{d}=\dfrac{2021a}{2021b}=\dfrac{2021a-c}{2021b-d}\)
c, Ta có \(\dfrac{a}{b}=\dfrac{c}{d}\Rightarrow\left(\dfrac{a}{b}\right)^2=\left(\dfrac{c}{d}\right)^2\)
Áp dụng t/c dtsbn:
\(\left(\dfrac{a}{b}\right)^2=\left(\dfrac{c}{d}\right)^2=\dfrac{a^2}{b^2}=\dfrac{c^2}{d^2}=\dfrac{a^2+c^2}{b^2+d^2}\)
Đúng 1
Bình luận (2)

mọi người ơi giúp mik với ai làm đc bài nào thì làm. làm xong mik tick cho
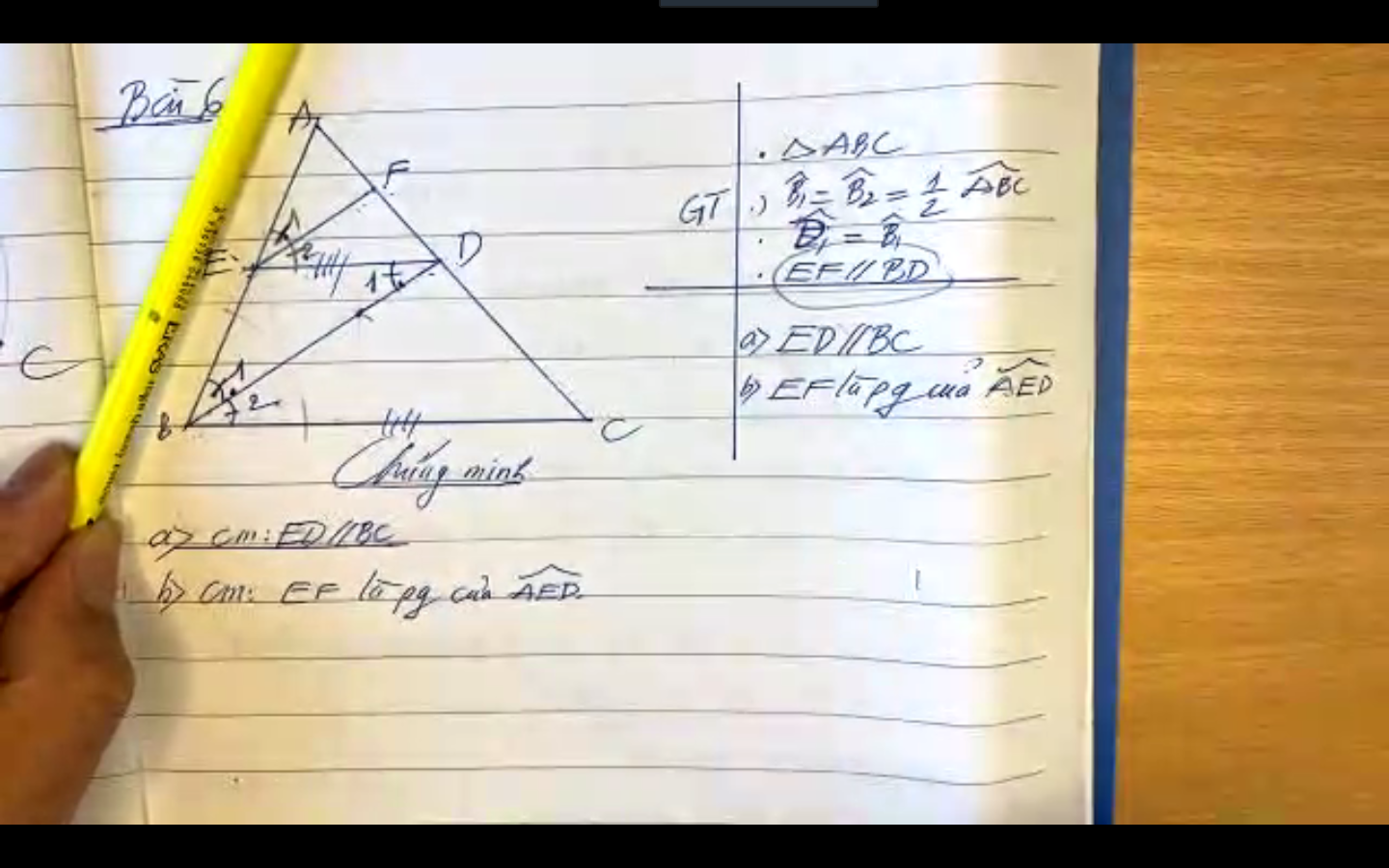
mọi người ơi , giúp mik phần b với ai làm đc thì mik tick cho
Mọi người ơi giúp mik những bài mik khoảnh tròn với ai làm đc bài nào mik tick cho.
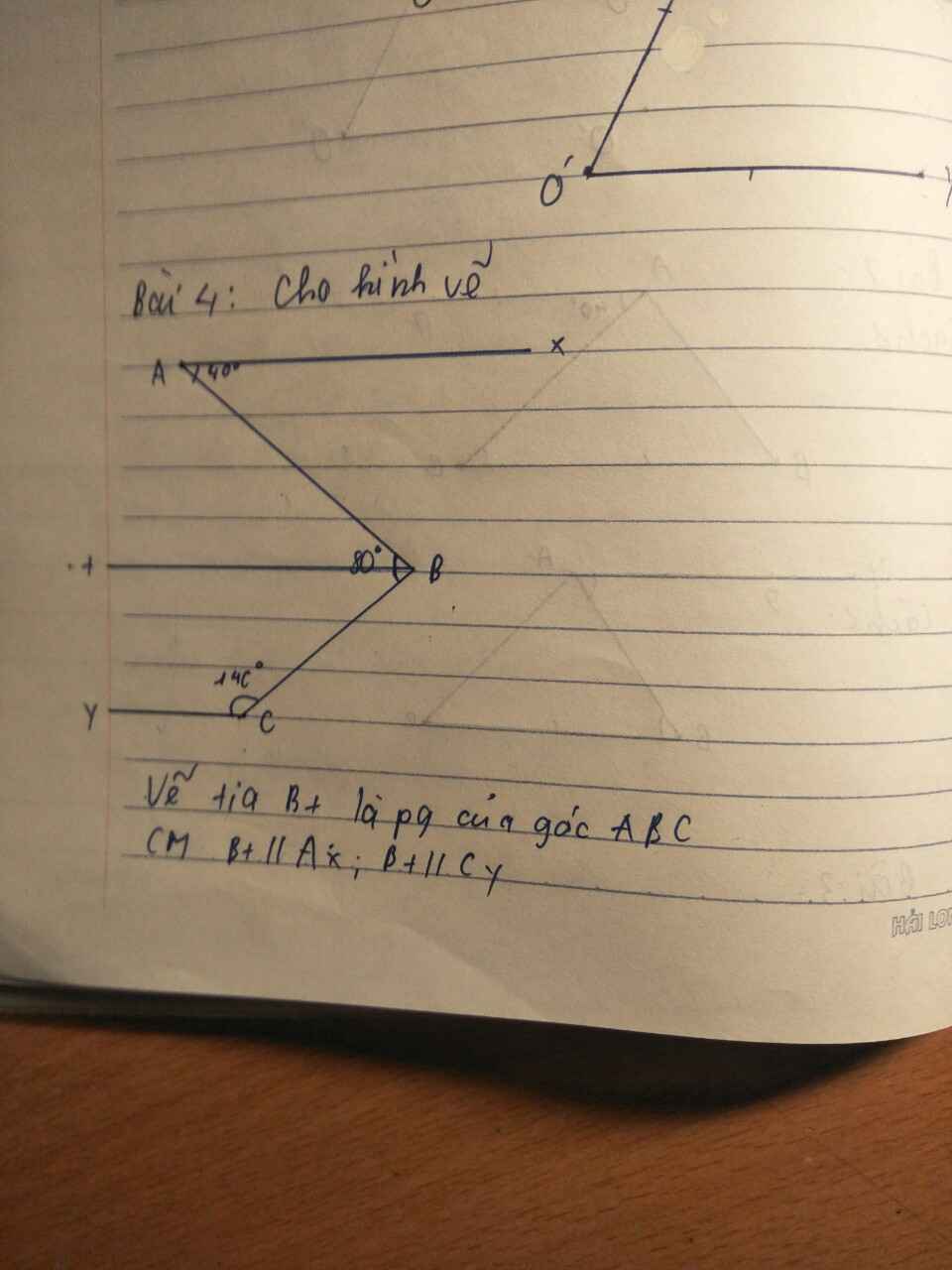
mọi người ơi giúp mik với , ai làm đc mik tick cho
Ta có: Bt là tia p/g của \(\widehat{ABC}\)
\(\Rightarrow\widehat{ABt}=\widehat{CBt}=\dfrac{\widehat{ABC}}{2}=80^0:2=40^0\)
Ta lại có: \(\widehat{BAx}=\widehat{ABt}=40^0\) (so le trong)
⇒Bt//Ax
Kẻ Ca là tia đối của Cy
Lại có: \(\widehat{BCa}\) kề bù với \(\widehat{BCy}\)
\(\Rightarrow\widehat{BCa}+\widehat{BCy}=180^0\)
\(\Rightarrow\widehat{BCa}+40^0=180^0\)
\(\Rightarrow\widehat{BCa}=140^0\)
Mà \(\widehat{CBt}=\widehat{BCa}=40^0\) và 2 góc này so le trong
Ca//Bt hay Cy//Bt
Đúng 1
Bình luận (3)
Mọi người ơi giúp mik với mik đang cần gấp ai làm đc mik tick cho
Cho A = 1 + 2 + 2\(^2\) + 2\(^3\) + ... + 2\(^{101}\)
So sánh A với 5 . 2\(^{100}\)
mọi người ơi giúp mik với ai làm đc mik tick cho nha
\(A=1+2+2^2+...+2^{101}\)
\(2A=2+2^2+...+2^{102}\)
\(2A=\left(2+2^2+...+2^{102}\right)-\left(1+2+2^2+...+2^{101}\right)\)
\(A=2^{102}-1\)
\(B=5.2^{100}>2^{102}\)
Mà \(2^{102}>2^{102}-1\)
Nên B>A
Đúng 1
Bình luận (0)

mọi người ơi giúp mik với ai làm đc bài nào thì giúp mik nha
Chứng minh rằng: nếu \(\dfrac{a}{b}=\dfrac{c}{d}\) thì \(\dfrac{a+b}{a}=\dfrac{c+d}{c}\)
mọi người ơi giúp mik với, ai làm đc mik tick cho
Ta có: \(\dfrac{a}{b}=\dfrac{c}{d}\Leftrightarrow\dfrac{b}{a}=\dfrac{d}{c}\)
\(\Leftrightarrow1+\dfrac{b}{a}=1+\dfrac{d}{c}\)
\(\Leftrightarrow\dfrac{a+b}{a}=\dfrac{c+d}{c}\)
Đúng 2
Bình luận (0)
\(\dfrac{a}{b}=\dfrac{c}{d}\Leftrightarrow\dfrac{a}{c}=\dfrac{b}{d}\)
Áp dụng t/c dtsbn:
\(\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{a+b}{c+d}\Leftrightarrow\dfrac{a+b}{a}=\dfrac{c+d}{c}\)
Đúng 2
Bình luận (0)







