Bài 7:

a: Xét ΔDEF có \(EF^2=DE^2+DF^2\)

nên ΔDEF vuông tại D

b: \(DK=\dfrac{DE\cdot DF}{EF}=4.8\left(cm\right)\)

FK=6.4(cm)

Bài IV:

1: Xét tứ giác MAOB có

\(\widehat{MAO}+\widehat{MBO}=90^0+90^0=180^0\)

=>MAOB là tứ giác nội tiếp

=>M,A,O,B cùng thuộc một đường tròn

2: Xét (O) có

MA,MB là các tiếp tuyến
Do đó: MA=MB

=>M nằm trên đường trung trực của AB(1)

Ta có: OA=OB

=>O nằm trên đường trung trực của AB(2)

Từ (1) và (2) suy ra MO là đường trung trực của BA

=>MO\(\perp\)AB tại H và H là trung điểm của AB

Xét ΔMAO vuông tại A có AH là đường cao

nên \(MH\cdot MO=MA^2\left(3\right)\)

Xét (O) có

ΔACD nội tiếp

AD là đường kính

Do đó: ΔACD vuông tại C

=>AC\(\perp\)CD tại C

=>AC\(\perp\)DM tại C

Xét ΔADM vuông tại A có AC là đường cao

nên \(MC\cdot MD=MA^2\left(4\right)\)

Từ (3) và (4) suy ra \(MA^2=MH\cdot MO=MC\cdot MD\)

3: Ta có: \(\widehat{MAI}+\widehat{OAI}=\widehat{OAM}=90^0\)

\(\widehat{HAI}+\widehat{OIA}=90^0\)(ΔAHI vuông tại H)

mà \(\widehat{OAI}=\widehat{OIA}\)

nên \(\widehat{MAI}=\widehat{HAI}\)

=>AI là phân giác của góc HAM

Xét ΔAHM có AI là phân giác

nên \(\dfrac{HI}{IM}=\dfrac{AH}{AM}\left(5\right)\)

Xét ΔOHA vuông tại H và ΔOAM vuông tại A có 

\(\widehat{HOA}\) chung

Do đó: ΔOHA đồng dạng với ΔOAM

=>\(\dfrac{OH}{OA}=\dfrac{HA}{AM}\)

=>\(\dfrac{OH}{OI}=\dfrac{AH}{AM}\left(6\right)\)

Từ (5) và (6) suy ra \(\dfrac{OH}{OI}=\dfrac{IH}{IM}\)

=>\(HO\cdot IM=IO\cdot IH\)

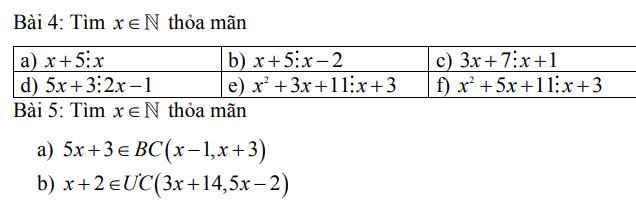
Bài 4:

\(a,\Rightarrow5⋮x\Rightarrow x\inƯ\left(5\right)=\left\{1;5\right\}\\ b,\Rightarrow x-2+7⋮x-2\\ \Rightarrow x-2\inƯ\left(7\right)=\left\{1;7\right\}\\ \Rightarrow x\in\left\{3;9\right\}\\ c,\Rightarrow3\left(x+1\right)+4⋮x+1\\ \Rightarrow x+1\inƯ\left(4\right)=\left\{1;2;4\right\}\\ \Rightarrow x\in\left\{0;1;3\right\}\\ d,\Rightarrow10x+6⋮2x-1\\ \Rightarrow5\left(2x-1\right)+11⋮2x-1\\ \Rightarrow2x-1\inƯ\left(11\right)=\left\{1;11\right\}\\ \Rightarrow x\in\left\{1;6\right\}\\ e,\Rightarrow x\left(x+3\right)+11⋮x+3\\ \Rightarrow x+3\inƯ\left(11\right)=\left\{1;11\right\}\\ \Rightarrow x=8\left(x\in N\right)\\ f,\Rightarrow x\left(x+3\right)+2\left(x+3\right)+5⋮x+3\\ \Rightarrow x+3\inƯ\left(5\right)=\left\{1;5\right\}\\ \Rightarrow x=2\left(x\in N\right)\)

6:

\(2^{225}=\left(2^3\right)^{75}=8^{75}\)

\(3^{150}=\left(3^2\right)^{75}=9^{75}\)

mà 8<9

nên \(2^{225}< 3^{150}\)

4: \(\left|5x+3\right|>=0\forall x\)

=>\(-\left|5x+3\right|< =0\forall x\)

=>\(-\left|5x+3\right|+5< =5\forall x\)

Dấu = xảy ra khi 5x+3=0

=>x=-3/5

1:

\(\left(2x+1\right)^4>=0\)

=>\(\left(2x+1\right)^4+2>=2\)

=>\(M=\dfrac{3}{\left(2x+1\right)^4+2}< =\dfrac{3}{2}\)

Dấu = xảy ra khi 2x+1=0

=>x=-1/2

lần đổ 1

\(\left(mC+m'C'\right).\left(38-20\right)=mC.\left(60-38\right)\)

\(\Leftrightarrow\left(mC+m'C'\right)18=mC.22\)

\(\Leftrightarrow2mC=9m'C'\)

lần 2 \(\left(2mC+m'C'\right)\left(t_x-38\right)=mC.\left(60-t_x\right)\)

\(11m'C'\left(t_x-38\right)=\dfrac{9}{2}.m'C'\left(60-t_x\right)\)

\(\Rightarrow t_x=...\)

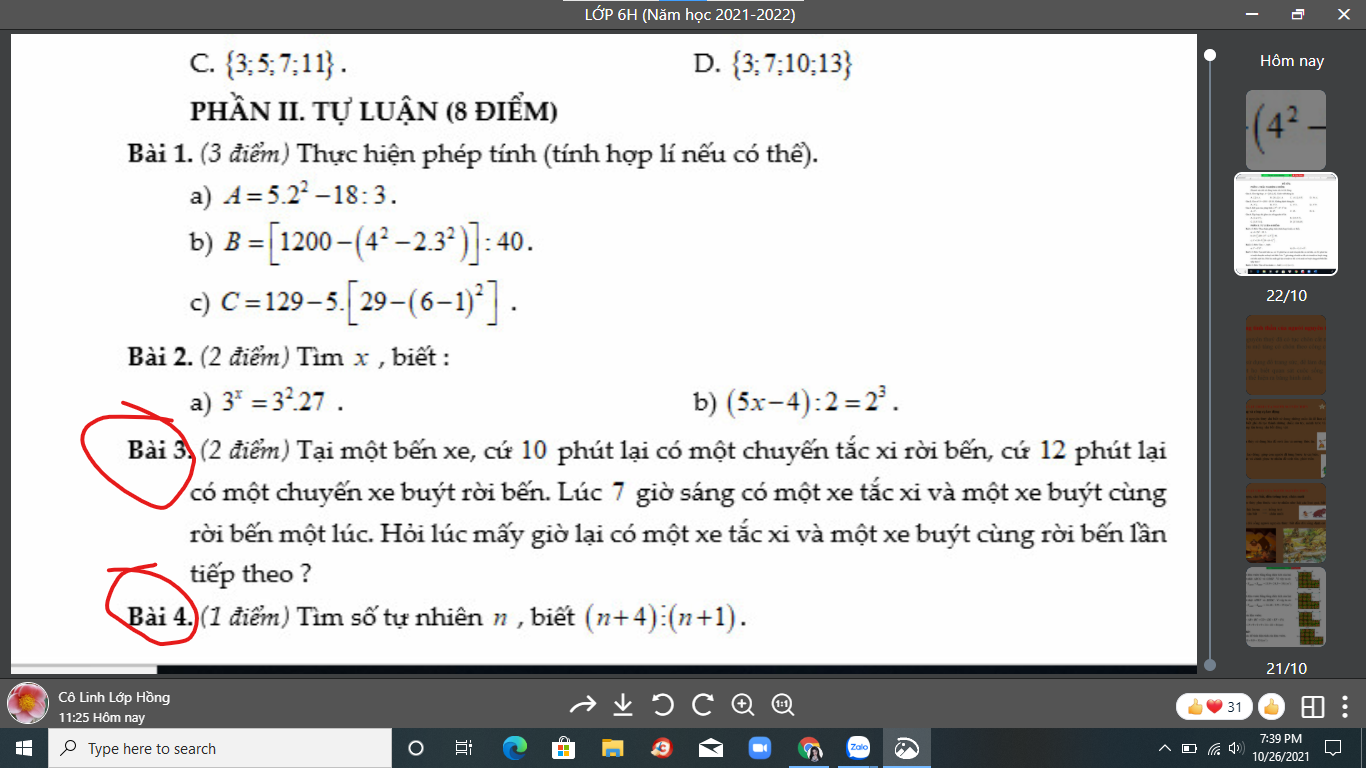
Bài 4:

\(\Leftrightarrow n+1\in\left\{1;3\right\}\)

hay \(n\in\left\{0;2\right\}\)

\(\left(n+4\right)⋮\left(n+1\right)\Rightarrow\left(n+1\right)+3⋮\left(n+1\right)\)

\(\Rightarrow\left(n+1\right)\inƯ\left(3\right)=\left\{-3;-1;1;3\right\}\)

Mà \(n\in N\)

\(\Rightarrow n\in\left\{0;2\right\}\)

Bài 4

\(n+4⋮n+1\)

\(n+1+3⋮n+1\)

\(\Rightarrow3⋮n+1\)

\(\Rightarrow n+1\inƯ\left(3\right)\)

\(Ư\left(3\right)=\left\{1;3\right\}\)

\(\Rightarrow n\in\left\{0;2\right\}\)