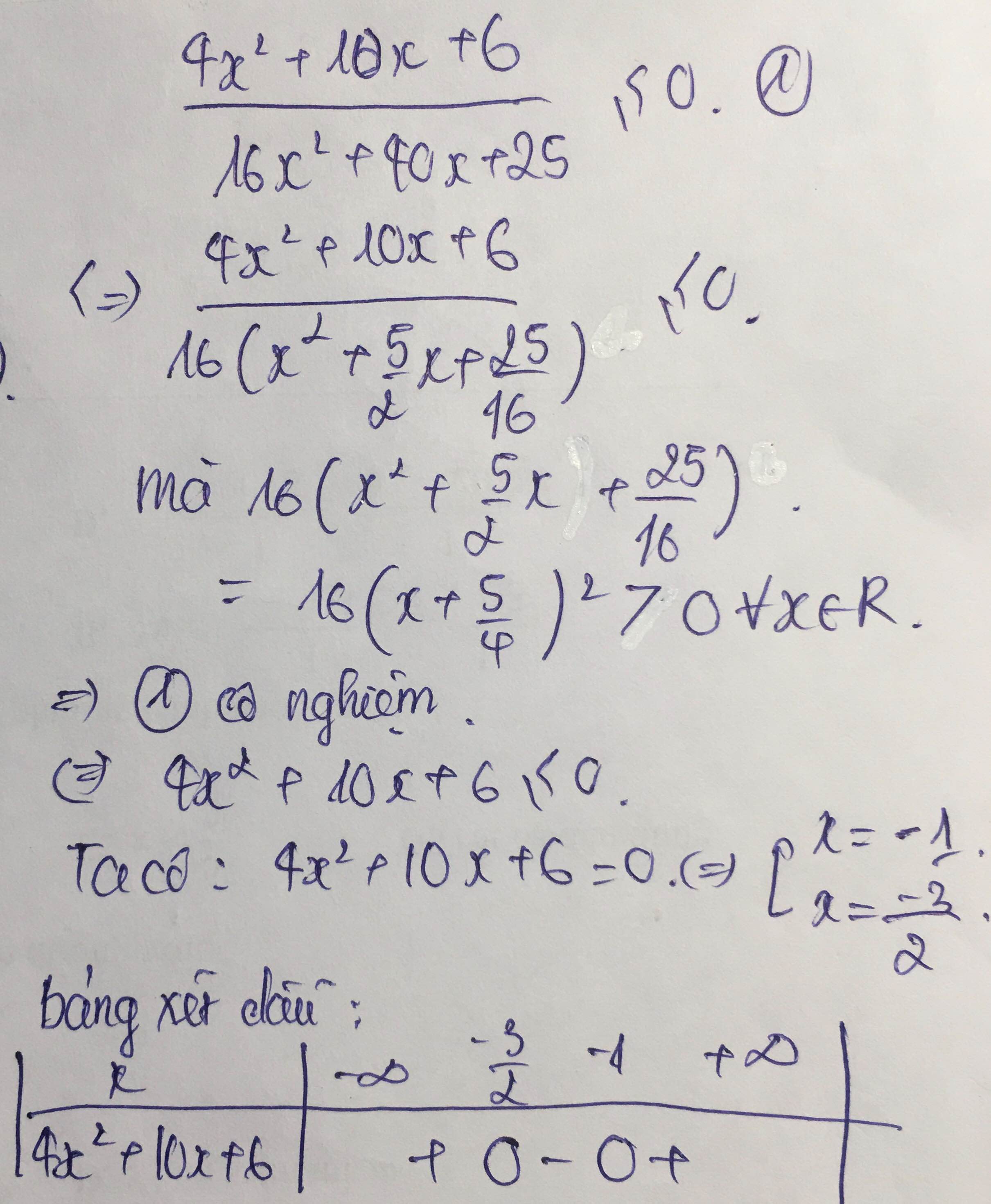a) 9-64x^2=0

=>  64x^2  = 8

=>  \(x^2=\frac{8}{64}=\frac{1}{8}\)

=> \(x=\frac{1}{\sqrt{8}}\)

 b )   25x^2  -  3  =  0

=>  25x^2  =  3 

=>  \(x^2=\frac{3}{25}\)    

=>  \(x=\frac{\sqrt{3}}{5}\)           

C)  7  -  16x^2  =0

=>  16x^2   =  7

=>  \(x^2=\frac{7}{16}\)       

=>   \(x=\frac{\sqrt{7}}{4}\)    

d)  4x^2  -  (x-4)^2 = 0

=>  4x^2  - x^2 + 8x - 16 =0

=>  3x^2 + 8x -16  =  0 

=> ( 3x^2 + 12x ) - ( 4x  +16 ) =  0 

=>  3x( x + 4 ) - 4( x + 4 ) =  0 

=>( x + 4 )( 3x - 4 ) =  0 

=>   \(\orbr{\begin{cases}x+4=0\\3x-4=0\end{cases}}\)    

=>  \(\orbr{\begin{cases}x=-4\\x=\frac{4}{3}\end{cases}}\)         

e)  ( 3x + 4 )^2 - ( 2x - 5 )^2 = 0

=>  ( 3x + 4 + 2x - 5 )( 3x + 4 - 2x + 5 )  = 0

=>   ( 5x -1 ) ( x + 9 )  = 0 

=>  \(\orbr{\begin{cases}5x-1=0\\x+9=0\end{cases}}\)     

=> \(\orbr{\begin{cases}x=\frac{1}{5}\\x=-9\end{cases}}\)            

Trả lời:

a, \(9-64x^2=0\)

\(\Leftrightarrow\left(3-8x\right)\left(3+8x\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}3-8x=0\\3+8x=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=\frac{3}{8}\\x=-\frac{3}{8}\end{cases}}}\)

Vậy x = 3/8; x = - 3/8 là nghiệm của pt.

b, \(25x^2-3=0\)

\(\Leftrightarrow\left(5x-\sqrt{3}\right)\left(5x+\sqrt{3}\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}5x-\sqrt{3}=0\\5x+\sqrt{3}=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=\frac{\sqrt{3}}{5}\\x=-\frac{\sqrt{3}}{5}\end{cases}}}\)

Vậy \(x=\pm\frac{\sqrt{3}}{5}\)

c, \(7-16x^2=0\)

\(\Leftrightarrow\left(\sqrt{7}-4x\right)\left(\sqrt{7}+4x\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}\sqrt{7}-4x=0\\\sqrt{7}+4x=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=\frac{\sqrt{7}}{4}\\x=-\frac{\sqrt{7}}{4}\end{cases}}}\)

Vậy \(x=\pm\frac{\sqrt{7}}{4}\)

d, \(4x^2-\left(x-4\right)^2=0\)

\(\Leftrightarrow\left(2x-x+4\right)\left(2x+x-4\right)=0\)

\(\Leftrightarrow\left(x+4\right)\left(3x-4\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}x+4=0\\3x-4=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-4\\x=\frac{4}{3}\end{cases}}}\)

Vậy x = - 4; x = 4/3 là nghiệm của pt.

e, \(\left(3x+4\right)^2-\left(2x-5\right)^2=0\)

\(\Leftrightarrow\left(3x+4-2x+5\right)\left(3x+4+2x-5\right)=0\)

\(\Leftrightarrow\left(x+9\right)\left(5x-1\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}x+9=0\\5x-1=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-9\\x=\frac{1}{5}\end{cases}}}\)

Vậy x = - 9; x = 1/5 là nghiệm của pt.

\(\Leftrightarrow\frac{\left(x+a\right)\left(3a^2x^2+a^2+8ax+x^2+3\right)\left(3a^6x^6+27a^6x^4+33a^6x2+a^6+72a^5x^5+24a^5x^3+72a^{5x}+27a^4x^6+459a^4x^4+441a^4x^2+33a^4+240a^3x^5+800a^3x^3+240a^3x+33a^2x^6+441a^2x^4+459x^2a^2+27a^2+75ax^5+240ax^3+72ax+x^6+33x^4+27x^2+3\right)}{\left(a^2+3\right)\left(a^6+33a^4+27a^{2+3}\right)\left(x^{2+3}\right)\left(x^6+33x^4+27x^2+3\right)}=0\)

mấy nhân tử sau ko cần chú ý đâu :)) chỉ cần chú ý đến x+a=0 <=>x=-a thôi :)) 

bài này đúng 100% nhé chỉ sợ gõ sai thôi, ko tin có thể dùng máy tính kiểm tra 

1. x³ + 8 = (x + 2 )(x² - x + 1)

2. 27 - 8y³ = ( 3 - 2y ) ( 9 + 6y + 4y² )

3. y⁶ + 1 = (y²)³ + 1 = ( y² + 1) ( y⁴ - y² +1 )

4.64x³ - \(\dfrac{1}{8}\)y³ = ( 4x - \(\dfrac{1}{2}\)y ) ( 16x² + 2xy + \(\dfrac{1}{4}\)y²)

5. 125x⁶ - 27y⁹ = (5x²)³ - (3y³)³

= ( 5x² - 3y³)(25x⁴ +15x²y³ + 9y⁶)

16x^4 - 40x^2y^3 + 25y^6

= ( 4x^2 - 5y^3 )^2 > hoặc = 0 với mọi giá trị của biến

Vậy ( 4x^2 - 5y^3 )^2 không âm

\(x^6-6x^4-64x^3+12x^2-8=0\)

\(\Leftrightarrow\left(x^2-4x-2\right)\left(x^4+4x^3+12x^2-8x+4\right)=0\)

\(\Leftrightarrow\left(x^2-4x-2\right)\left[\left(x^4+4x^3+4x^2\right)+\left(8x^2-8x+\frac{8}{4}\right)+2\right]=0\)

\(\Leftrightarrow\left(x^2-4x-2\right)\left[\left(x^2+2x\right)^2+8\left(x-\frac{1}{2}\right)^2+2\right]=0\)

\(\Leftrightarrow x^2-4x-2=0\)

\(\Leftrightarrow x=2\pm\sqrt{6}\)

a) \(\sqrt{x^2}=7\)

\(\Leftrightarrow\left|x\right|=7\)

\(\Leftrightarrow\orbr{\begin{cases}x=7\\x=-7\end{cases}}\)

b) \(\sqrt{\left(x-2020\right)^2}=10\)

\(\Leftrightarrow\left|x-2020\right|=10\)

\(\Leftrightarrow\orbr{\begin{cases}x-2020=10\\x-2020=-10\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=2030\\x=2010\end{cases}}\)

c) đk: \(x\ge2\)

 \(\sqrt{4}-\left(x-2\right)+3\sqrt{16x-32}=8\)

\(\Leftrightarrow2-x+2+12\sqrt{x-2}=8\)

\(\Leftrightarrow12\sqrt{x-2}=x+4\)

\(\Leftrightarrow144\left(x-2\right)=\left(x+4\right)^2\)

\(\Leftrightarrow x^2-136x+304=0\)

\(\Leftrightarrow\orbr{\begin{cases}x_1=133,726...\\x_2=2,273...\end{cases}}\)

d) đk: \(x\ge-1\)

 \(\sqrt{25x+25}-2\sqrt{64x+64}=7\)

\(\Leftrightarrow5\sqrt{x+1}-16\sqrt{x+1}=7\)

\(\Leftrightarrow-11\sqrt{x+1}=7\)

Mà \(-11\sqrt{x+1}\le0< 7\left(\forall x\right)\)

=> pt vô nghiệm