Câu a em tự học thành tài nhé

b. 

+) Giao điểm giữa (d) và Ox là: A( a; 0) 

=> 0 = \(\frac{3}{4}\)a - 3  => a = 4 

=> A (4; 0) => OA = |4 | = 4 

+  Giao điểm giữa (d) và Oy là: B( 0; b) 

=> b = \(\frac{3}{4}\).0 - 3  => b = -3 

=> B (0; -3) => OB = | - 3| = 3

Xét tam giác OAB vuông tại O => S (OAB) = \(\frac{1}{2}.OA.OB=\frac{1}{2}.3.4=6\left(đ.v.d.t\right)\)

c. Kẻ OH vuông AB => OH là khoảng cách từ O đến (d) 

=> \(\frac{1}{OH^2}=\frac{1}{OA^2}+\frac{1}{OB^2}=\frac{1}{3^2}+\frac{1}{4^2}=\frac{25}{144}\)

=> OH = 2,4 

Vậy khoảng cách từ O đến (d) là 2,4 

a) Ta có: \(y=2x+1\)

\(+)a=2>0;b=1\) 

Đồ thị hàm số cắt: \(Ox\left(-\dfrac{1}{2};0\right);Oy\left(0;1\right)\)

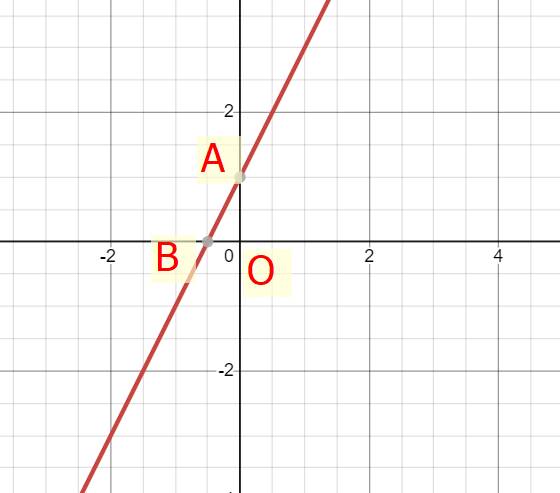
b) Gọi giao điểm của hàm số với trục Ox là B, với trục Oy là A 

Xét tam giác OAB vuông tại O ta có: \(\left\{{}\begin{matrix}OA=1\\OB=\dfrac{1}{2}\end{matrix}\right.\)

\(\Rightarrow S_{OAB}=\dfrac{1}{2}\cdot1\cdot\dfrac{1}{2}=\dfrac{1}{4}\left(đvdt\right)\)  

c) Gọi khoảng cách từ O đến (d) là đường cao OH của tam giác OAB ta có: 

\(\dfrac{1}{OH^2}=\dfrac{1}{OA^2}+\dfrac{1}{OB^2}\)

\(\Rightarrow OH^2=\dfrac{OA^2OB^2}{OA^2+OB^2}=\dfrac{1^2\cdot\left(\dfrac{1}{2}\right)^2}{1^2+\left(\dfrac{1}{2}\right)^2}=\dfrac{1}{5}\)

\(\Rightarrow OH=\sqrt{\dfrac{1}{5}}=\dfrac{\sqrt{5}}{5}\)

Gợi ý :

a) y = 2 => x = 2 hoặc -2 ( do có thể < 0 hay > 0 )

b) S(OAB) = 1 => |x| = 1 => x = 1 hoặc -1

c) Gọi khoảng cách từ O tới (d) là OH

OH bé hơn hoặc bằng khoảng cách 2 của O tới điểm cố định trên Oy

=> max = 2 khi d song^2 Ox => x = 0 => đúng mọi m

d)  Thay vào biểu thức hệ thức lượng => khoảng cách từ O tới điểm mà d cắt trên Ox là 0 => d trùng Oy

e) thay x vào có kết quả

f) cắt tại điểm > 2 => biểu thức biểu diễn x > 2 ( -2/(m+3)   )

a, Hình vẽ

b, Gọi \(A=\left(d\right)\cap Ox;B=\left(d\right)\cap Oy\) ta cần tính \(S_{OAB}\)

\(x=0\Rightarrow y=-3\Rightarrow B\left(0;-3\right)\in\left(d\right)\Rightarrow OB=3\)

\(x=4\Rightarrow y=0\Rightarrow A\left(4;0\right)\in\left(d\right)\Rightarrow OA=4\)

\(S_{\Delta OAB}=\frac{1}{2}.OA.OB=\frac{1}{2}.4.3=6\)

c, Gọi H là chân đường vuông góc kẻ từ O đến \(\left(d\right)\)

Ta có \(\frac{1}{OH^2}=\frac{1}{OA^2}+\frac{1}{OB^2}=\frac{1}{16}+\frac{1}{9}=\frac{25}{144}\Rightarrow OH=\frac{12}{5}\)

HELP ♥