Question

cho đường thẳng (d):y=2x+1
a) vẽ đường thẳng (d)
b)tính diện tích tam giác được tạo thành giữa đường thẳng (d) và hai trục tọa độ
c) tính khoảng cách từ gốc O đến đường thẳng (d)

Answer 1

a) Ta có: \(y=2x+1\)

\(+)a=2>0;b=1\) 

Đồ thị hàm số cắt: \(Ox\left(-\dfrac{1}{2};0\right);Oy\left(0;1\right)\)

 

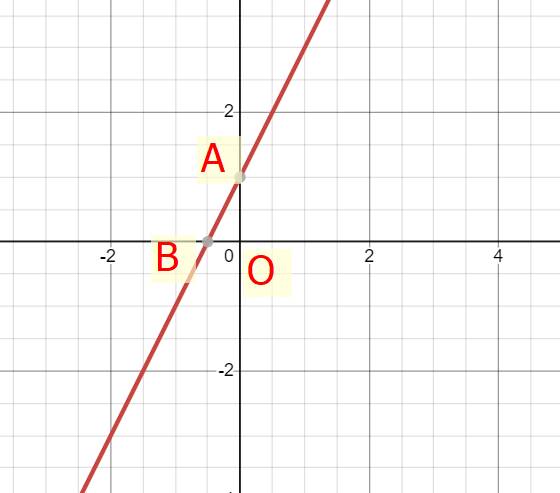
b) Gọi giao điểm của hàm số với trục Ox là B, với trục Oy là A 

Xét tam giác OAB vuông tại O ta có: \(\left\{{}\begin{matrix}OA=1\\OB=\dfrac{1}{2}\end{matrix}\right.\)

\(\Rightarrow S_{OAB}=\dfrac{1}{2}\cdot1\cdot\dfrac{1}{2}=\dfrac{1}{4}\left(đvdt\right)\)  

c) Gọi khoảng cách từ O đến (d) là đường cao OH của tam giác OAB ta có: 

\(\dfrac{1}{OH^2}=\dfrac{1}{OA^2}+\dfrac{1}{OB^2}\)

\(\Rightarrow OH^2=\dfrac{OA^2OB^2}{OA^2+OB^2}=\dfrac{1^2\cdot\left(\dfrac{1}{2}\right)^2}{1^2+\left(\dfrac{1}{2}\right)^2}=\dfrac{1}{5}\)

\(\Rightarrow OH=\sqrt{\dfrac{1}{5}}=\dfrac{\sqrt{5}}{5}\)