a:
Vẽ đồ thị y=2-x
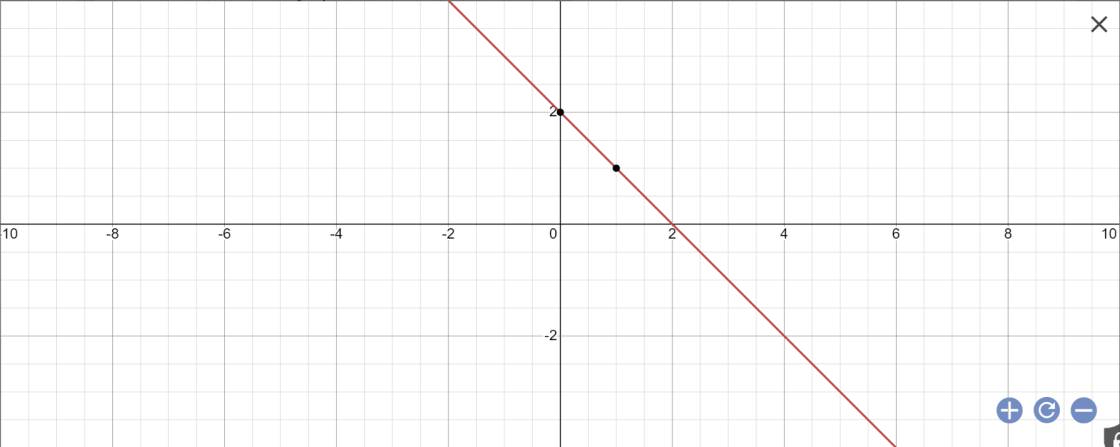
y=2-x
=>y+x-2=0
=>x+y-2=0
Khoảng cách từ O đến đường thẳng x+y-2=0 là:
\(d\left(O;x+y-2=0\right)=\dfrac{\left|0\cdot1+0\cdot1-2\right|}{\sqrt{1^2+1^2}}\)
\(=\dfrac{2}{\sqrt{1+1}}=\dfrac{2}{\sqrt{2}}=\sqrt{2}\)
b:
Vẽ đồ thị y=2x+1
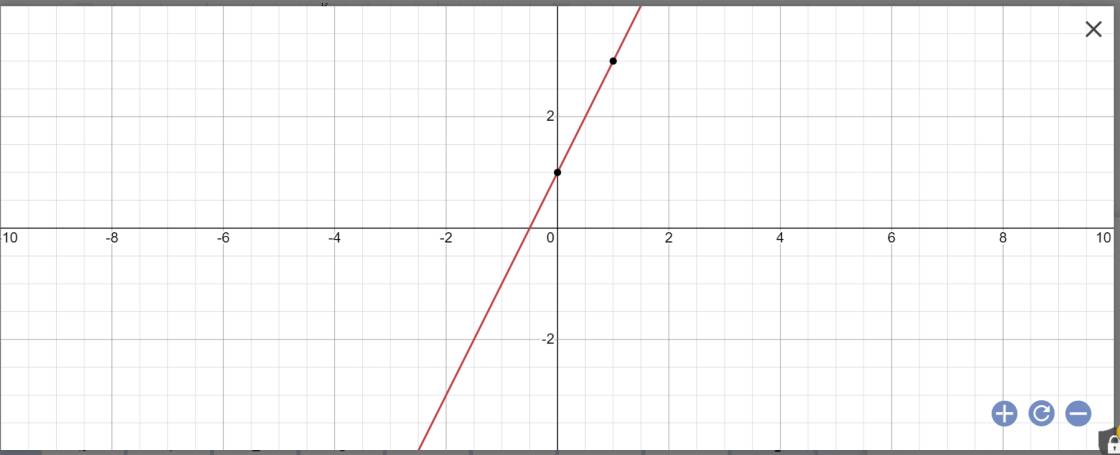
y=2x+1
=>2x-y+1=0
Khoảng cách từ O(0;0) đến đường thẳng y=2x+1 là:
\(\dfrac{\left|0\cdot2+0\cdot\left(-1\right)+1\right|}{\sqrt{2^2+\left(-1\right)^2}}=\dfrac{1}{\sqrt{4+1}}=\dfrac{\sqrt{5}}{5}\)
c:
Vẽ đồ thị \(y=\dfrac{x-2}{2}\)
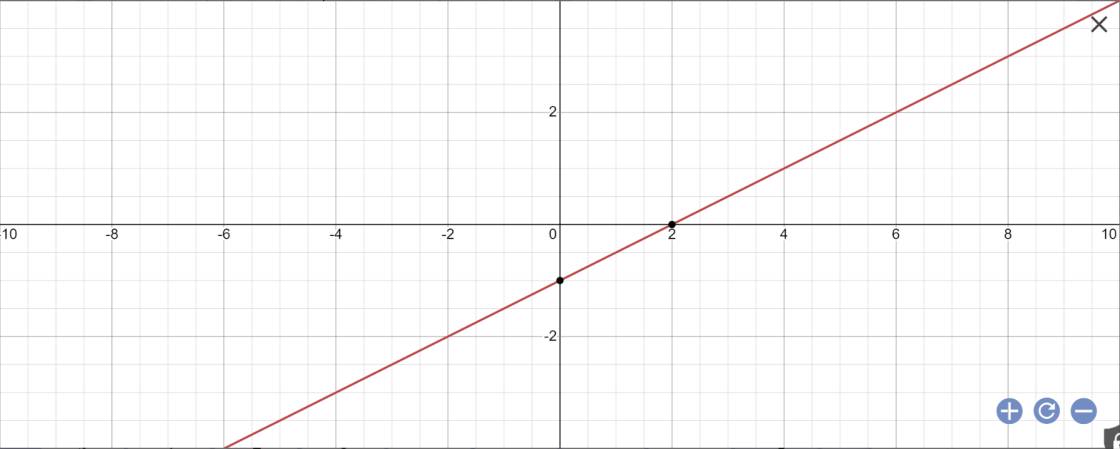
\(y=\dfrac{x-2}{2}\)
=>x-2=2y
=>x-2y-2=0
Khoảng cách từ O(0;0) đến đường thẳng \(y=\dfrac{x-2}{2}\) là:
\(\dfrac{\left|0\cdot1+0\cdot\left(-2\right)-2\right|}{\sqrt{1^2+\left(-2\right)^2}}=\dfrac{\left|-2\right|}{\sqrt{1+4}}=\dfrac{2}{\sqrt{5}}\)
d:
Vẽ đồ thị y=-2x
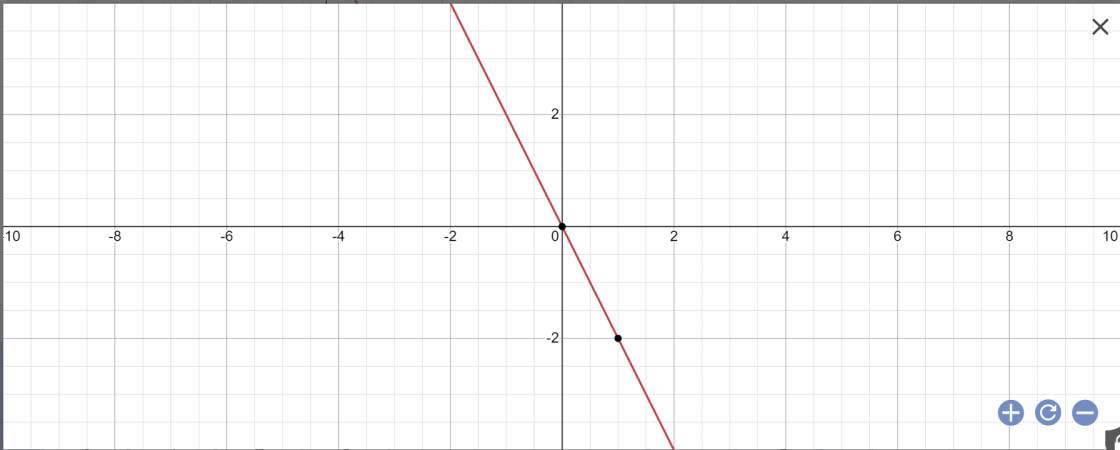
y=-2x
=>-2x+y=0
Khoảng cách từ O(0;0) đến đường thẳng y=-2x là:
\(\dfrac{\left|0\cdot\left(-2\right)+0\cdot1+0\right|}{\sqrt{\left(-2\right)^2+1^2}}=\dfrac{0}{\sqrt{\left(-2\right)^2+1^2}}=0\)






