Question

Cho đường thẳng d và hai điểm A, B có khoảng cách đến đường thẳng d theo thứ tự là 20cm và 6cm. Gọi C là trung điểm của AB. Tính khoảng cách từ C đến đường thẳng d.

Answer 1

Trường hợp A và B nằm trên hai nửa mặt phẳng đối bờ chứa đường thẳng d

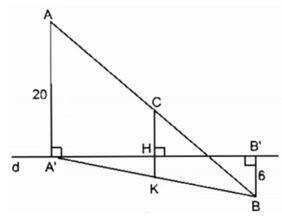
Kẻ CH ⊥ d cắt A'B tại K

⇒ CH // AA' // BB'

Trong ∆ AA'B ta có: AC = CB

Mà CK // AA' nên A'K = KB và CK là đường trung bình của tam giác AA'B

⇒CK= AA'/2 (tính chất đường trung bình của tam giác)

CK = 20/2 = 10(cm)

Trong  ∆ A'BB' có A'K = KB và KH // BB'

Nên KH là đường trung bình của  ∆ A'BB'

⇒ KH = BB'/2 (tính chất đường trung bình của tam giác)

⇒ KH = 6/2 =3 (cm)

CH = CK – KH = 10 – 3 = 7(cm)