Nửa khoảng \([a;b)\) là tập hợp tất cả giá trị cuẩ m để hệ bất phương trình \(-1\le\frac{x^2+5x+m}{2x^2-3x+2}< 7\) nghiệm đúng với tất cả giá trị x.
Tìm a và b
Những câu hỏi liên quan
Nêu định nghĩa đoạn [a; b], khoảng (a; b), nửa khoảng [a; b), (a; b], (-∞; b], [a; +∞). Viết tập hợp R các số dưới dạng một khoảng.
- Đoạn: [a; b] = {x ∈ R | a ≤ x ≤ b}
- Khoảng: (a; b) = {x ∈ R | a < x < b}
- Nửa khoảng:
[a; b) = {x ∈ R | a ≤ x < b}
(a; b] = {x ∈ R | a < x ≤ b}
(-∞; b] = {x ∈ R | x ≤ b}
[a; +∞) = {x ∈ R | x ≥ a}
- Tập hợp R = (-∞; +∞)
Đúng 0
Bình luận (0)
Bài 12: Một ôtô chạy trên đoạn đường thẳng từ A đến B phải mất khoảng thời gian t. Tốc
độ của ôtô trong nửa đầu của khoảng thời gian này là 60km/h. Trong nửa khoảng thời gian
cuối là 40km/h. Tính tốc độ trung bình trên cả đoạn AB.
Vận tốc trung bình của ô tô là:
Ta có: \(v_{tb}=\dfrac{s_1+s_2}{t_1+t_2}=\dfrac{\dfrac{v_1t}{2}+\dfrac{v_2t}{2}}{t}=\dfrac{v_1+v_2}{2}=\dfrac{60+40}{2}=50\left(km/h\right)\)
Đúng 3
Bình luận (0)
Trong nửa thời gian đầu: S1=v1.t1=60.t/2=30t
Trong nửa thời gian cuối: S2=v2.t2=40.t/2=20t
Mà ta có: vtb=\(\dfrac{S}{t}=\dfrac{S_1+S_2}{t_1+t_2}=\dfrac{30t+20t}{t}=50\)
Đúng 1
Bình luận (0)
Cho đường thẳng b. Gọi a và a’ là hai đường thẳng song song với đường thẳng b và cùng cách đường thẳng b một khoảng bằng h (h.94), (I) và (II) là các nửa mặt phẳng bờ b. Gọi M, M’ là các điểm cách đường thẳng b một khoảng bằng h, trong đó M thuộc nửa mặt phẳng (I), M’ thuộc nửa mặt phẳng (II). Chứng minh rằng M ∈ a, M’ ∈ a’.
Đọc tiếp
Cho đường thẳng b. Gọi a và a’ là hai đường thẳng song song với đường thẳng b và cùng cách đường thẳng b một khoảng bằng h (h.94), (I) và (II) là các nửa mặt phẳng bờ b. Gọi M, M’ là các điểm cách đường thẳng b một khoảng bằng h, trong đó M thuộc nửa mặt phẳng (I), M’ thuộc nửa mặt phẳng (II). Chứng minh rằng M ∈ a, M’ ∈ a’.
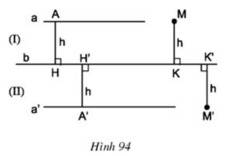
Góc AHH’ = góc HH’A’ (= 90o). Mà 2 góc đó là 2 góc so le trong
⇒ a // b
Và a // a’
⇒ a’ // b
- Tứ giác AMKH có AH = MK (= h) và AH // MK (cùng ⊥ b)
⇒ Tứ giác AMKH là hình bình hành ⇒ AM // HK
Mà a // b ⇒ a // HK
Do đó AM trùng với a hay M ∈ a
- Chứng minh tương tự: M’ ∈ a’
Đúng 0
Bình luận (0)
Một ôtô chạy trên đoạn đường thẳng từ A đến B phải mất khoảng thời gian t. Trong nửa đầu của khoảng thời gian này ô tô có tốc độ là 60km/h. Trong nửa khoảng thời gian cuối ô tô có tốc độ là 40km/h. Tính tốc độ trung bình trên cả đoạn AB. A.
v
t
b
20
k
m
/
h
B.
v...
Đọc tiếp
Một ôtô chạy trên đoạn đường thẳng từ A đến B phải mất khoảng thời gian t. Trong nửa đầu của khoảng thời gian này ô tô có tốc độ là 60km/h. Trong nửa khoảng thời gian cuối ô tô có tốc độ là 40km/h. Tính tốc độ trung bình trên cả đoạn AB.
A. v t b = 20 k m / h
B. v t b = 30 k m / h
C. v t b = 40 k m / h
D. v t b = 50 k m / h
Một ô tô chạy trên đoạn đường thẳng từ A đến B phải mất khoảng thời gian t. Tốc độ của ô tô trong nửa đầu của khoảng thời gian này là 60km/h. Trong nửa khoảng thời gian cuối là 40km/h. Tính tốc độ trung bình trên cả đoạn đường AB.
I will help :))
\(S1=v1.t1=60.\frac{1}{2}t=30t\) ( km )
\(S2=v2.t2=40.\frac{1}{2}t=20t\left(km\right)\)
\(AB=S1+S2=30t+20t=50t\)
\(Vtb=\frac{S}{t}=\frac{50t}{t}=50\left(\frac{km}{h}\right)\)
:))
Đúng 1
Bình luận (0)
Vận tốc trung bình của ô tô trên cả quãng đường là :
(60 + 40) : 2 = 50 (km/giờ)
Vậy Vận tốc trung bình của ô tô trên cả quãng đường là : 50 km/giờ
Đúng 0
Bình luận (7)
Một ôtô chạy trên đoạn đường thẳng từ A đến B phải mất khoảng thời gian t. Trong nửa đầu của khoảng thời gian này ô tô có tốc độ là 60km/h. Trong nửa khoảng thời gian cuối ô tô có tốc độ là 40km/h. Tính tốc độ trung bình trên cả đoạn AB
Một ôtô chạy trên đoạn đường thẳng từ A đến B phải mất khoảng thời gian t. Trong nửa đầu của khoảng thời gian này ô tô có tốc độ là 60km/h. Trong nửa khoảng thời gian cuối ô tô có tốc độ là 40km/h. Tính tốc độ trung bình trên cả đoạn AB.
Giải:
Trong nửa thời gian đầu: S 1 = v 1 . t 1 = 60. t 2 = 30 t
Trong nửa thời gian cuối: S 2 = v 2 . t 2 = 40. t 2 = 20 t
Mà ta có: v t b = S t = S 1 + S 2 t 1 + t 2 = 30 t + 20 t t = 50 k m / h
Đúng 0
Bình luận (0)
Cho hai nửa khoảng A=( -2;0] và B=[0;2). Tìm AvB,. AnB , A\B
\(A\cup B=\left(-2;2\right)\)
\(A\cap B=\left\{0\right\}\)
\(A\B=\left(-2;0\right)\)
Đúng 1
Bình luận (0)
Cho tập hợp A = { x \(\in R\) | x \(\le-12\) } được viết dưới dạng đoạn, khoảng, nửa khoảng là:
A. A = ( \(-\infty\) ; -12 ] B. A = {.... ; -10; -11; -12 } C. A = (\(-\infty\) ; -12 ) D. A = [ -12; \(+\infty\) ]
ai giảng lại cho em về Nửa khoảng:[a,b)={
