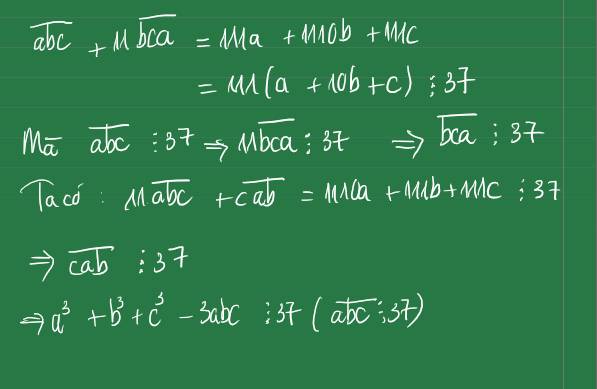Ta có abc chia hết cho 27 thì abc0 chia hết cho 27. 
-> a000 + bc0 chia hết cho 27 
-> 1000.a +bc0 chia hết cho 27 
-> 999.a + a + bc0 chia hết cho 27 
-> 37 x 27 x a + bca chia hết cho 27 
Do 37 x 27 x a chia hết cho 27 nên bca chia hết cho 27.

chứng minh:bca⋮37

bca=b.100+c.10+a

bca=b.100+c.10+a.1

bca=(b+c+a).(100+10+1)

bca=(b+c+a).111

bca=(b+c+a).3.37

⇒bca⋮37

a) 327, * = 2

b) 279, * = 9

327 hay  357 hay 387 đều chia hết cho 3.

270 hay 279 đều chia hết cho 9.

a) *∈{2;5;8}

b)*∈{0;9}

vì abc chia hết cho 27, mà \(27=3^3\)=> abc phải chia hết cho 3

để abc chia hết cho 3 <=> a+b+c \(⋮\)3

do abc chia hết cho 3 phụ thuộc vào tổng các chữ số

=> \(abc⋮3\Rightarrow bca⋮3\)hay bca chia hết cho 27

abc chia hết cho 27 

\(\Rightarrow\)( 100a + 10b + c ) chia hết cho 27

\(\Rightarrow\)10 . ( 100a + 10b + c ) chia hết cho 27

\(\Rightarrow\)1000a + 100b + 10c chia hết cho 27

\(\Rightarrow\)999a + ( 100b + 10c + a ) chia hết cho 27

Mà 999a chia hết cho 27 \(\Rightarrow\)bca chia hết cho 27 .

Giả sử \(\overline{abc}\)chia hết cho 27 thì trước hết \(\overline{abc}\)phải chia hết cho 9 \(\Rightarrow\)a + b + c chia hết cho 9 

\(\Rightarrow\overline{bca}\)cũng chia hết cho 9 \(\Rightarrow\overline{bca}=9m\left(m\in N\right)\)

Theo bài ra ta có :

 \(\Leftrightarrow\left(100a+10b+c\right)-\left(100b+10c+a\right)=9\left(3k-m\right)\)

\(\Leftrightarrow99a-90b-9c=9\left(3k-m\right)\)

\(\Leftrightarrow11a-10b-c+m=3k\)

\(\Leftrightarrow21a-10\left(a+b+c\right)+9c+m=3k\)

Vế phải chia hết cho 3 mà các số : \(21a;10\left(a+b+c\right)\)và \(9c\)đều chia hết cho 3 

\(\Rightarrow m\)cũng chia hết cho 3

\(\Rightarrow m=3n\left(n\in N\right)\)

\(\Rightarrow\overline{bca}=9m=27n\)

\(\Rightarrow\overline{bca}\)chia hết cho 27 ( đpcm ) 

a, Ta có:

\(\overline{ab}+\overline{ba}=10a+b+10b+a=11\left(a+b\right)\)

=> ab + ba chia hết cho 11(đpcm)

b, Ta có:
\(\overline{ab}-\overline{ba}=10a+b-10b-a=9\left(a-b\right)\)

=> ab - ba chia hết cho 9 (a > b)(đpcm)

Chúc bạn học tốt!!!

c) Câu hỏi của Mai Trung Kiên - Toán lớp 6 - Học toán với OnlineMath

tham khảo nhé bạn

\(\overline{ab}+\overline{ba}=10a+b+10b+a=11.a+11.b=11\left(a+b\right)⋮11\rightarrowđpcm\)\(\overline{ab}-\overline{ba}=10a+b-10b-a=9a-9b=9\left(a-b\right)⋮9\rightarrowđpcm\)

\(\overline{abc}⋮27\Rightarrow\overline{abc}⋮3^3\Rightarrow\overline{abc}⋮3\)

\(\Rightarrow a+b+c⋮3\Rightarrow b+c+a⋮3\)

\(\Rightarrow\overline{bca}⋮3\rightarrowđpcm\)

a, ab + ba= ( 10a +b )+ (10b+a ) = 11a + 11b= 11(a+b) chia hết cho 11

Vậy ab+ba chia hết cho 11

b, ab - ba = (10a + 10b ) + ( 10b + a ) = 9a+9b= 9 (a+b) chia hết cho 9

Vậy ab - ba chia hết cho9