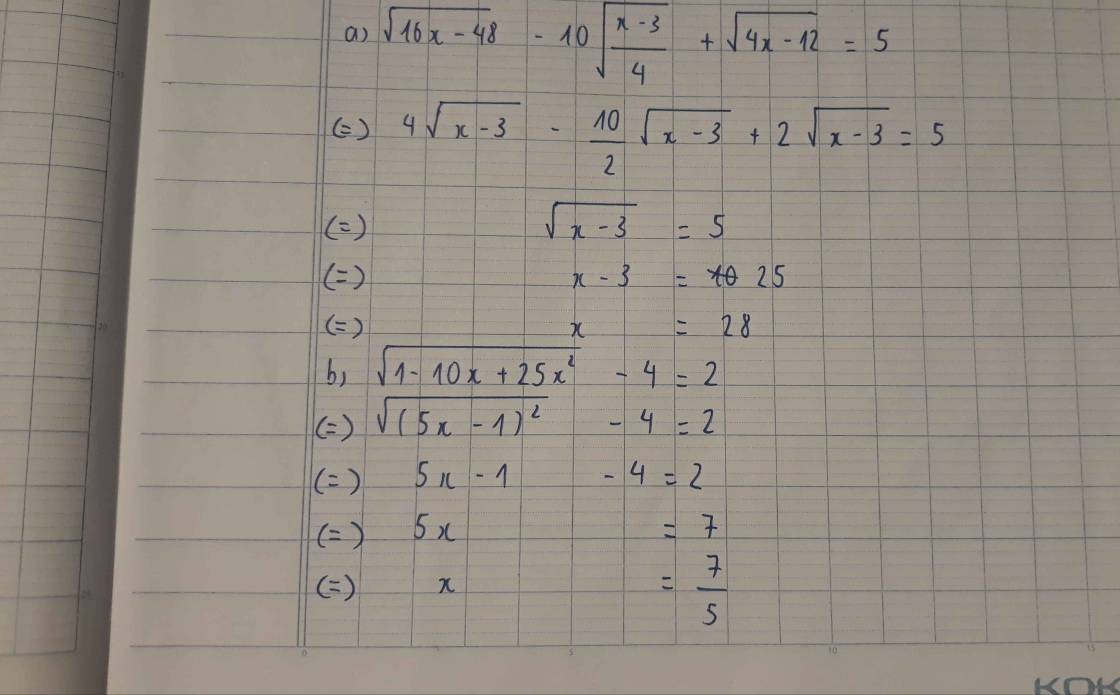ĐKXĐ: x >= 2

Pt <=> 3sqrt(x - 2) = 6

<=> sqrt(x - 2) = 2

<=> x - 2 = 4

<=> x = 6 (thỏa ĐKXĐ)

\(\Leftrightarrow\left(x+1\right)\sqrt{3x+1}-5\sqrt{2x-1}+\sqrt{2x-1}\cdot\sqrt{3x+1}-5\left(x+1\right)=0\)

\(\Leftrightarrow\left(x+1\right)\left(\sqrt{3x+1}-5\right)+\sqrt{2x-1}\cdot\left(\sqrt{3x+1}-5\right)=0\)

\(\Leftrightarrow\left(x+1+\sqrt{2x-1}\right)\left(\sqrt{3x+1}-5\right)=0\)

\(\Leftrightarrow\hept{\begin{cases}\left(x+1+\sqrt{2x-1}\right)=0\\\sqrt{3x+1}-5=0\end{cases}}\Leftrightarrow\hept{\begin{cases}vônghiệm\\x=8\end{cases}}\)

Đk : \(x\ge\frac{1}{2}\)

Đặt \(\sqrt{2x-1}=a;\sqrt{3x+1}=b\)\(a\ge0;b>0\)  thì x+1 = b²-a²-1

PT<=> (b^2-a^2-1)b -5a + ab = 5(b^2-a^2-1)

    <=> (b^2-a^2-1)(b-5)+a(b-5)=0

    <=> (b^2-a^2-1+a)(b-5)=0

    <=>\(\orbr{\begin{cases}b^2-a^2-1+a=0\\b-5=0\end{cases}}\)

* b^2-a^2-1+a= 0 <=>x+2 -1 + \(\sqrt{2x-1}\)=0<=> x+1+\(\sqrt{2x-1}\)=0

Mặt khác : x\(\ge\)1/2 >0 ; \(\sqrt{2x-1}\ge0\) nên x+1+\(\sqrt{2x-1}>0\)=> pt vô no

*b-5 = 0 <=> b=5 <=> x= 8 tm

Vậy pt có no duy nhất là x=8

mk làm dài nên làm theo bn kia

Điều kiện x>=-2; y>=0; x>=y-3

Ta xét PT thứ nhất 

Đặt √(x+2) = a; √y = b (a,b>=0)

Thì PT thành a(a² - b² + 1) - b = 0

<=> a³ - ab² + a - b = 0

<=> a(a - b)(a + b) + (a -b) =0

<=> (a - b)(a² + ab + 1)=0

Đễ thấy a² + ab + 1 >0

Nên a =b 

Thế vào ta được y = x + 2

Thay cái này vào PT còn lại là xong

\(\hept{\begin{cases}\sqrt{x+2}\left(x-y+3\right)=\sqrt{y}\left(1\right)\\x^2+\left(x+3\right)\left(2x-y+5\right)=x+16\left(2\right)\end{cases}}\)
DKXD :x>=-2; y>=0
Đặt\(\hept{\begin{cases}\sqrt{x+2=a}\\x-y+3=b\end{cases}\left(a\ge0\right)}\)
Pt 1 có dạng \(ab=\sqrt{a^2-b+1}\Leftrightarrow a^2b^2=a^2-b+1\Leftrightarrow a^2\left(b-1\right)\left(b+1\right)+b-1=0\)
\(\Leftrightarrow\left(b-1\right)\left(a^2b+a^2+1\right)=0\)
+> b-1=0\(\Rightarrow b=1\Leftrightarrow x-y+3=1\)
\(\)Khi đó pt (2) \(\Leftrightarrow x^2+\left(x+3\right)\left(x+2+1\right)=x+16\Leftrightarrow x^2+\left(x+3\right)^2=x+16\)
\(\Leftrightarrow x^2+x^2+6x+9=x+16\Leftrightarrow2x^2+5x-7=0\)
Có : 2+5-7=0
Nên pt trên có 2 no \(x_1=1\left(tm\right);x_2=-\frac{7}{2}\left(ktm\right)\)
\(\Rightarrow1-y+3=1\Leftrightarrow y=3\left(tm\right)\)
+>\(a^2b+a^2+1=0\Leftrightarrow\left(x+2\right)\left(x+3-y\right)+x+3=0\)(3)
Đặt \(x+3=m\). Pt(3) có dạng \(\left(m-1\right)\left(m-y\right)+m=0\Leftrightarrow m^2-m-my+y+m=0\Leftrightarrow m^2=y\left(m-1\right)\)
Nếu \(m-1=0\Leftrightarrow x+3-1=0\Leftrightarrow x=-2\left(tm\right)\Rightarrow y=0\left(tm\right)\)
Nhưng k tm pt 2
\(\Rightarrow m-1\ne0\Rightarrow y=\frac{m^2}{m-1}=\frac{\left(x+3\right)^2}{x+2}\)
Thay vào pt (2) ta được \(x^2+\left(x+3\right)\left(2x+5-\frac{\left(x+3\right)^2}{x+2}\right)=x+16\)
ĐẾn đây tự nhân chéo chuển vế ta được \(2x^3+7x^2-8x-29=0\)

Cảm ơn bạn nhưng mình lỡ k cho bb kia rồi

Xin lỗi nhìu nha 

\(\sqrt[3]{5+x}-x=5\)

\(\Leftrightarrow\sqrt[3]{5+x}=5+x\)

\(\Leftrightarrow5+x=125+75x+15x^2+x^3\)

\(\Leftrightarrow125+75x+15x^2+x^3-5-x=0\)

\(\Leftrightarrow120+74x+15x^2+x^3=0\)

\(\Leftrightarrow\left(x+4\right)\left(x+5\right)\left(x+6\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-4\\x=-5\\x=-6\end{matrix}\right.\)

b.

ĐKXĐ: \(x\ge-1\)

\(\sqrt{\left(x+1\right)\left(x+35\right)}-14\sqrt{x+35}+84-6\sqrt{x+1}=0\)

\(\Leftrightarrow\sqrt{x+1}\left(\sqrt{x+35}-14\right)-6\left(\sqrt{x+35}-14\right)=0\)

\(\Leftrightarrow\left(\sqrt{x+1}-6\right)\left(\sqrt{x+35}-14\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x+1}=6\\\sqrt{x+35}=14\end{matrix}\right.\)

\(\Leftrightarrow...\)

a. ĐKXĐ: \(-1\le x\le1\)

Đặt \(\left\{{}\begin{matrix}\sqrt{x+1}=a\ge0\\\sqrt{1-x}=b\ge0\end{matrix}\right.\)

\(\Rightarrow a+2a^2=-b^2+b+3ab\)

\(\Leftrightarrow\left(2a^2-3ab+b^2\right)+a-b=0\)

\(\Leftrightarrow\left(a-b\right)\left(2a-b\right)+a-b=0\)

\(\Leftrightarrow\left(a-b\right)\left(2a-b+1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}a=b\\2a+1=b\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x+1}=\sqrt{1-x}\\2\sqrt{x+1}+1=\sqrt{1-x}\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\\4x+5+4\sqrt{x+1}=1-x\left(1\right)\end{matrix}\right.\)

(1) \(\Leftrightarrow4\sqrt{x+1}=-4-5x\) \(\left(x\le-\dfrac{4}{5}\right)\)

\(\Leftrightarrow16\left(x+1\right)=25x^2+40x+16\)

\(\Leftrightarrow25x^2+24x=0\Rightarrow\left[{}\begin{matrix}x=0\left(loại\right)\\x=-\dfrac{24}{25}\end{matrix}\right.\)

c.

ĐKXĐ: \(x\ge-\dfrac{3}{2}\)

\(\Leftrightarrow x\sqrt{2x+3}-\sqrt{2x+3}+3-3x+3\sqrt{x+5}-\sqrt{\left(2x+3\right)\left(x+5\right)}=0\)

\(\Leftrightarrow\sqrt{2x+3}\left(x-1\right)-3\left(x-1\right)-\sqrt{x+5}\left(\sqrt{2x+3}-3\right)=0\)

\(\Leftrightarrow\left(x-1\right)\left(\sqrt{2x+3}-3\right)-\sqrt{x+5}\left(\sqrt{2x+3}-3\right)=0\)

\(\Leftrightarrow\left(x-1-\sqrt{x+5}\right)\left(\sqrt{2x+3}-3\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x-1-\sqrt{x+5}=0\\\sqrt{2x+3}-3=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x+5-\sqrt{x+5}-6=0\\\sqrt{2x+3}=3\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x+5}=-2\left(loại\right)\\\sqrt{x+5}=3\\\sqrt{2x+3}=3\end{matrix}\right.\)

\(\Leftrightarrow...\)

\(\Leftrightarrow x^2+4=2x+3\)

=>x^2-2x+1=0

=>(x-1)^2=0

=>x=1

\(VT=\sqrt{\left(\sqrt{x+2}-1\right)^2+3}+\sqrt{\left(\sqrt{x+2}-3\right)^2}>\sqrt{3}>1\) pt vô nghiệm