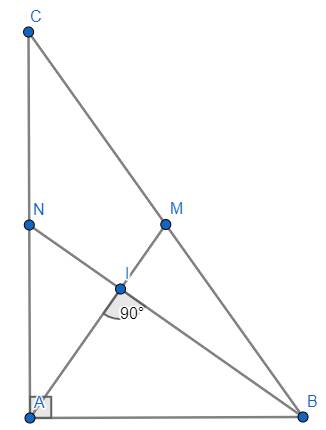
Cho ΔABC vuông tại A (AB<AC) đường cao AH đường trung tuyến AM. Đường tròn (H;HA) cắt AC tại E và cắt tia đối BA tại D. Gọi O là tâm đường tròn ngoại tiếp tứ giác BECD. Chứng minh AHOM là hình bình hành

Những câu hỏi liên quan
Bài1:Cho ΔMNP vuông tại N. Tính độ dài MN biết MP√30cm,NP√14 cmBài2:Cho ΔABC cân tại A. Biết AB2cm. Tính BCBài3:Cho ΔABC vuông tại A,AH⊥BC tại H. Tính độ dài các cạnh của ΔABC biết AH6cm,HB4cm,HC9cmBài4:Cho ΔABC vuông tại A,AH⊥BC tại H. Tính độ dài các cạnh của ΔABC biết AH4cm,HB2cm,HC8cmBài5:Cho ΔABC vuông tại A,AH⊥BC tại H.Biết AB4cm,HB2cm,HC8cm.Tính BC,AH,ACBài6:Cho ΔABC vuông tại A,AH⊥BC tại H.Biết AB6cm,AC8cm và dfrac{HB}{HC}dfrac{9}{16}Tính HB,HC
Đọc tiếp
Bài1:Cho ΔMNP vuông tại N. Tính độ dài MN biết MP=√30cm,NP=√14 cm
Bài2:Cho ΔABC cân tại A. Biết AB=2cm. Tính BC
Bài3:Cho ΔABC vuông tại A,AH⊥BC tại H. Tính độ dài các cạnh của ΔABC biết AH=6cm,HB=4cm,HC=9cm
Bài4:Cho ΔABC vuông tại A,AH⊥BC tại H. Tính độ dài các cạnh của ΔABC biết AH=4cm,HB=2cm,HC=8cm
Bài5:Cho ΔABC vuông tại A,AH⊥BC tại H.Biết AB=4cm,HB=2cm,HC=8cm.Tính BC,AH,AC
Bài6:Cho ΔABC vuông tại A,AH⊥BC tại H.Biết AB=6cm,AC=8cm và \(\dfrac{HB}{HC}\)=\(\dfrac{9}{16}\)Tính HB,HC
Bài 3:
\(AB=\sqrt{AH^2+BH^2}=\sqrt{6^2+4^2}=2\sqrt{13}\left(cm\right)\)
BC=13cm
=>\(AC=3\sqrt{13}\left(cm\right)\)
Đúng 0
Bình luận (0)
* Cho ΔABC vuông tại A có B= \(30^0\), AB=6cm
a. Giải ΔABC
b. Vẽ đường cao AH và trung tuyến AM của ΔABC. Tính diện tích ΔAHM
* Cho ΔABC vuông tại A có AB=3 cm, BC=5cm, đường cao AH
a. Tính số đo góc B, C
b. Gọi AE là phân giác của góc A (E ∈ BC). Tính AE
Bài 1:
a: Xét ΔBAC vuông tại A có
\(\widehat{B}+\widehat{C}=90^0\)
hay \(\widehat{C}=60^0\)
Xét ΔBAC vuông tại A có
\(AB=BC\cdot\sin60^0\)
\(\Leftrightarrow BC=4\sqrt{3}\left(cm\right)\)
\(\Leftrightarrow AC=2\sqrt{3}\left(cm\right)\)
Đúng 1
Bình luận (0)
Cho ΔABC vuông tại B biết: BC=2a; góc A=45°: a) Tính độ dài cạnh AB; AC b) Kẻ BH vuông góc AC. Tính BH=? c) Tính diện tích ΔABC d) Tính chu vi ΔABC e) Tính bán kính đường tròn ngoại tiếp ΔABC
a: ΔBAC vuông tại B có góc A=45 độ
nên ΔBAC vuông cân tại B
=>BA=BC=2a
AC=căn AB^2+BC^2=2a*căn 2
b: BH=BA*BC/AC=4a^2/2*a*căn 2=a*căn 2
c: S ABC=1/2*2a*2a=2a^2
d: C=2a+2a+2a*căn 2=4a+2a*căn 2
Đúng 0
Bình luận (0)
Cho tam giác ΔABC vuông tại A có AB=6cm,AC=10cm . Đường cao AH a)Chứng minh ΔABC / ΔABH b)Chứng minh AB²=BH.BC c)Tính BC,AH,BH
a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
Do đó: ΔABC\(\sim\)ΔHBA
b: ta có: ΔABC\(\sim\)ΔHBA
nên BA/BH=BC/BA
hay \(BA^2=BH\cdot BC\)
Đúng 1
Bình luận (0)
a.Xét tam giác ABC và tam giác HBA, có:
^B: chung
^BAC = ^BHA = 90 độ
Vậy tam giác ABC đồng dạng tam giác HBA (g.g)
b.\(\rightarrow\dfrac{AB}{HB}=\dfrac{BC}{AB}\)
\(\Leftrightarrow AB^2=BH.BC\left(đfcm\right)\) (1)
c.Áp dụng định lý pitago \(\Rightarrow BC=\sqrt{6^2+10^2}=2\sqrt{34}\left(cm\right)\)
(1) \(\Leftrightarrow6^2=2\sqrt{34}BH\)
\(\Leftrightarrow BH=\dfrac{9\sqrt{34}}{17}\left(cm\right)\)
Áp dụng định lý pitago trong tam giác ABH \(\Rightarrow AH=\sqrt{6^2-\left(\dfrac{9\sqrt{34}}{17}\right)^2}=\dfrac{15\sqrt{34}}{17}\left(cm\right)\)
Đúng 0
Bình luận (0)
Cho ΔABC vuông tại A. Chứng minh: Tan \(\dfrac{ABC}{2}=\dfrac{AB}{AB+BC}\)
Kẻ phân giác BK
Xét ΔABK vuông tại A có
\(\tan\widehat{ABK}=\dfrac{AK}{AB}\)
\(\Leftrightarrow\tan\dfrac{\widehat{ABC}}{2}=\dfrac{AK}{AB}\)(1)
Xét ΔABC có BK là đường phân giác ứng với cạnh AC(gt)
nên \(\dfrac{AK}{AB}=\dfrac{KC}{BC}\)(Tính chất đường phân giác)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AK}{AB}=\dfrac{KC}{BC}=\dfrac{AK+KC}{AB+BC}=\dfrac{AC}{AB+BC}\)(2)
Từ (1) và (2) suy ra \(\tan\dfrac{\widehat{ABC}}{2}=\dfrac{AC}{AB+BC}\)
Đúng 2
Bình luận (0)
Cho ΔABC vuông tại A có AB > AC, M là điểm tuỳ ý trên BC. Qua M kẻ Mx vuông góc với BC và cắt AB tại I cắt CA tại D.
a. Chứng minh ΔABC đồng dạng với ΔMDC
b. Chứng minh: BI.BA = BM.BC
c. Cho góc ACB = 60o và SΔCDB = 60 cm². Tính SΔCMA.
a: Xét ΔCMD vuông tại M và ΔCAB vuông tại A có
góc C chung
=>ΔCMD đồng dạng với ΔCAB
b: Xét ΔBMI vuông tại M và ΔBAC vuông tại A có
góc MBI chung
=>ΔBMI đồng dạng với ΔBAC
=>BM/BA=BI/BC
=>BM*BC=BA*BI
c: ΔCMD đồng dạng với ΔCAB
=>CM/CA=CD/CB
=>CM/CD=CA/CB
=>ΔCMA đồng dạng với ΔCDB
=>S CMA/S CDB=(CA/CB)^2=1/4
=>S CMA=15cm2
Đúng 0
Bình luận (0)
Cho ΔABC vuông tại A, AB = a. Các đường trung tuyến AM và BN vuông góc với nhau. Tính AB và BC theo a.
Gọi \(I\) là giao điểm của \(AM\) và \(BN\Rightarrow IB=\dfrac{2}{3}BN;IN=\dfrac{1}{3}BN;AI=\dfrac{2}{3}AM;IM=\dfrac{1}{3}AM\)
\(\Delta ANB\) vuông tại \(A:AI^2=IB.IN\) \(\Rightarrow AI^2=\dfrac{2}{3}BN\cdot\dfrac{1}{3}BN=\dfrac{2}{9}BN^2\)
Ta cũng có trong \(\Delta ANB:AB^2=IB.BN\)
\(\Leftrightarrow a^2=\dfrac{2}{3}BN\cdot BN=\dfrac{2}{3}BN^2\Leftrightarrow BN^2=\dfrac{3}{2}a^2\)
Suy ra : \(AI^2=\dfrac{2}{9}BN^2=\dfrac{2}{9}\cdot\dfrac{3}{2}a^2=\dfrac{1}{3}a^2\).
Lại có : \(AI=\dfrac{2}{3}AM\Rightarrow AM^2=\dfrac{9}{4}AI^2=\dfrac{9}{4}\cdot\dfrac{1}{3}a^2=\dfrac{3}{4}a^2\)
\(AM\) là đường trung tuyến ứng với cạnh huyền \(BC\) của \(\Delta ABC\) vuông tại \(A\Rightarrow AM=\dfrac{1}{2}BC\Rightarrow BC^2=4AM^2=4\cdot\dfrac{3}{4}a^2=3a^2\)
\(\Rightarrow BC=\sqrt{3a^2}=a\sqrt{3}\)
\(\Delta ABC\) vuông tại \(A\) có : \(BC^2=AB^2+AC^2\left(Pythagoras\right)\)
\(\Rightarrow AC=\sqrt{BC^2-AB^2}=\sqrt{3a^2-a^2}=a\sqrt{2}\)
Vậy : \(AC=a\sqrt{2};BC=a\sqrt{3}\)
Đúng 1
Bình luận (0)
: Cho ΔABC vuông tại A có AB = 5cm, AC = 12cm.
a/ Tính BC.
b/ Trên tia đối của tia AB lấy điểm D sao cho AD = AB. Chứng minh ΔABC = ΔADC.
c/ Chứng minh : BCD cân tại C.
d/ Vẽ đường thẳng qua A song song với BC cắt CD tại E, BE cắt AC tại G. Chứng minh : G là
trọng tâm của BDC. ( Dành cho các lớp 7 A, B, C)
CÂU D THOI CX ĐC:))
a: \(BC=\sqrt{AB^2+AC^2}=13\left(cm\right)\)
b: Xét ΔABC vuông tại A và ΔADC vuông tại A có
AC chung
AB=AD
Do đó: ΔABC=ΔADC
c: Ta có: ΔABC=ΔADC
nên BC=DC
hay ΔCBD cân tại C
Đúng 0
Bình luận (0)
cho ΔABC vuông tại A. Trên tia đối tia AB, lấy điểm sao cho AD=AB
a. cm= ΔABC=ΔADC
b. Trên tia đối tia AC lấy điểm E sao cho AE=AC. Chứng minh BC//DE
a: Xét ΔABC vuông tại A và ΔADC vuông tại A có
AB=AD
AC chung
Do đó: ΔABC=ΔADC
b: Xét tứ giác BCDE có
A là trung điểm của BD
A là trung điểm của CE
Do đó: BCDE là hình bình hành
Suy ra: BC//DE
Đúng 1
Bình luận (0)
cho ΔABC vuông tại A, biết AB=3cm, AC=4 cm, đường trung tuyến AD ( D ∈BC). Gọi M và N lần lượt là hình chiếu của D Trên AB và AC
a) tính BC, AD
b) chứng minh AD=MN
c) nếu ΔABC vuông cân tại A thì tứ giác BMNC là hình gì ? tại sao ?
a. Pytago: \(BC=\sqrt{AB^2+AC^2}=5\left(cm\right)\)
AD là trung tuyến ứng cạnh huyền BC nên \(AD=\dfrac{1}{2}BC=2,5\left(cm\right)\)
b. Vì \(\widehat{AMD}=\widehat{AND}=\widehat{MAN}=90^0\) nên AMDN là hcn
Vậy AD=MN
c. ABC vuông cân A thì AD là trung tuyến cũng là p/g
Do đó AMDN là hình thoi(1)
Lại có D là trung điểm BC,DM//AC(⊥AB) nên M là trung điểm AB
Cmtt ta được N là trung điểm AC
Mà AB=AC nên AM=AC
Kết hợp (1) ta được AMDN là hình vuông
Đúng 3
Bình luận (0)