Bài tập 1:
Cho tam giác ABC nhọn, kẻ BE \(\perp\) AC tại E và CD \(\perp\) AB tại D , Gọi H là giao điểm của BE và CD. Kẻ HM \(\perp\) BC tại M
a, Chứng minh : A, H, M, thẳng hàng
b, Chứng minh BH.BE+CH.CD=BC\(^{^2}\)
Bài1: Cho Tam giác ABC nhọn , kẻ \(BE\perp AC\) tại E và \(CD\perp AB\)tại D. Gọi H là giao điểm của BE và CD, Kẻ\(HM\perp BC\) tại M.
a, Chứng minh 3 điểm A, H, M thẳng hàng
b, Chứng minh: \(BH.BE+CH.CD=BC^2\)
Bài 2: Cho tam giác ABC ( AB<AC ), đường phân giác AD. Vẽ tia Dx sao cho \(\widehat{CDx}=\widehat{BAC}\) (tia Dx và điểm A cùng phía đối với BC), tia Dx cắt AC ở E. Chứng minh :
a, Tam giác ABC đồng dạng tam giác DEC
b, DE=DB
bạn tự vẽ hinh nha
1)
Xét tam giác ABC có
hai đường cao BE và CD cắt nhau tại H nên H là trực tâm
do đó \(AH\perp BC\)
mà \(HM\perp BC\)
suy ra AH trùng với HM
vậy A; H; M thẳng hàng
b)
dễ chứng minh tam giác BHM đồng dạng với tam giác BCE \(\Rightarrow\frac{BH}{BC}=\frac{BM}{BE}\Rightarrow BH\cdot BE=BC\cdot BM\left(1\right)\)
dễ chứng minh tam giác CHM đồng dạng với tam giác CBD \(\Rightarrow\frac{CH}{BC}=\frac{CM}{CD}\Rightarrow CH\cdot CD=CM\cdot BC\left(2\right)\)
Từ (1) và (2) suy ra \(BH\cdot BE+CH\cdot CD=BM\cdot BC+CM\cdot BC=\left(BM+CM\right)\cdot BC=BC\cdot BC=BC^2\)
2)
a)
Xét tam giác ABC và tam giác DEC
có \(\widehat{BAC}=\widehat{CDE}\)
\(\widehat{ACB}\)chung
nên tam giác ABC đồng dạng với tam giác DEC
\(\Rightarrow\frac{AB}{DE}=\frac{AC}{CD}\left(1\right)\)
b)
Xét tam giác ABC
có AD là đường phân giác
\(\Rightarrow\frac{BD}{CD}=\frac{AB}{AC}\Rightarrow\frac{AB}{BD}=\frac{AC}{CD}\left(2\right)\)
Từ (1) và (2) suy ra
\(\frac{AB}{DE}=\frac{AB}{BD}\Rightarrow DE=BD\)
cho tam giác ABC nhọn kẻ BE vuông góc AC tại E và CD vuông góc AB tại D gọi H là giao điểm của BE va CD kẻ HM vuông góc BC tại M
a) cm 3 điểm A,H,M thẳng hàng
b) cm BE.BH+CH.CD=BC^2
a) Xét ΔABC có
BE là đường cao ứng với cạnh AC(gt)
CD là đường cao ứng với cạnh AB(gt)
BE cắt CD tại H(gt)
Do đó: H là trực tâm của ΔABC(Tính chất ba đường cao của tam giác)
Suy ra: AH\(\perp\)BC
mà HM\(\perp\)BC(gt)
và AH,HM có điểm chung là H
nên A,H,M thẳng hàng(đpcm)
b) Xét ΔBMH vuông tại M và ΔBEC vuông tại E có
\(\widehat{EBC}\) chung
Do đó: ΔBMH\(\sim\)ΔBEC(g-g)
Suy ra: \(\dfrac{BM}{BE}=\dfrac{BH}{BC}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(BE\cdot BH=BM\cdot BC\)
Xét ΔCMH vuông tại M và ΔCDB vuông tại D có
\(\widehat{DCB}\) chung
Do đó: ΔCMH\(\sim\)ΔCDB(g-g)
Suy ra: \(\dfrac{CM}{CD}=\dfrac{CH}{CB}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(CH\cdot CD=CM\cdot CB\)
Ta có: \(BE\cdot BH+CM\cdot CD\)
\(=BM\cdot BC+CM\cdot BC\)
\(=BC^2\)(đpcm)
Bài tập 95: Cho tam giác ABC vuông tại A, kẻ \(AH\perp BC\) tại H . Lấy điểm E đối xứng với điểm H qua AB và lấy điểm F đối xứng với điểm H qua AC
a, Chứng minh: E, A, F thẳng hàng
b, Chứng minh:\(AH^2=HB.HC\)
Bài tập 130: Cho tam giác ABC vuông tại A, kẻ \(AH\perp BC\) tại H. Tia phân giác của góc HAC cắt BC tại D, tia phân giác của góc HAB cắt BC ở E. Kẻ EM\(\perp\)AB tại M. Chứng minh rằng:
a, Tam giác BME đồng dạng tam giác AHC
b, Tam giác AEC cân
c, DH.EC=AH.DC
d, AB+AC=BC+DE
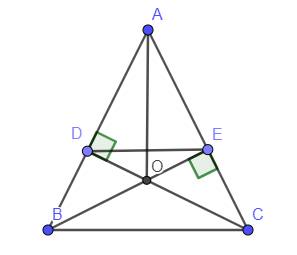
Cho tam giác ABC có AB = AC, từ điểm B kẻ \(BE\perp\) AC tại E, từ điểm C kẻ CD \(\perp\) AD tại D.
a) Chứng minh BD = CE
b) Đoạn BD cắt đoạn BE tại O.Chứng minh tam giác OBD = tam giác OCE
c) Chứng minh DE // BC
#\(N\)
*Sửa đề: `CD \bot AB` chứ không phải `AD, BE` cắt đoạn `CD` tại `O` chứ không phải đoạn `BD.`
`a,` Vì Tam giác `ABC` có `AB = AC ->`\(\widehat{B}=\widehat{C}\)
Xét Tam giác `BDC` và Tam giác `CEB` có:
`BC` chung
\(\widehat{B}=\widehat{C}\) `(CMT)`
\(\widehat{BDC}=\widehat{CEB}=90^0\)
`=>` Tam giác `BDC =` Tam giác `CEB (ch-gn)`
`-> BD = CE (2` cạnh tương ứng `)`
`b,` Xét Tam giác `ADC` và Tam giác `AEB` có:
`AB = AC (g``t)`
\(\widehat{A}\) chung
\(\widehat{AEB}=\widehat{ADC}=90^0\)
`=>` Tam giác `ADC =` Tam giác `AEB (ch-gn)`
`=>` \(\widehat{ABE}=\widehat{ACD}\) `( 2` góc tương ứng `)`
Xét Tam giác `OBD` và Tam giác `OCE` có:
\(\widehat{ODB}=\widehat{OEC}=90^0\)
`BD = CE (CMT)`
\(\widehat{DBO}=\widehat{ECO}\) `(CMT)`
`=>` Tam giác `OBD =` Tam giác `OCE (g-c-g)`
`c,` *Mình sẽ bổ sung sau nha bạn .-. câu này mình bị bí á .-.
lm nốt câu c nha=))
c:
Có `Delta OBD=Delta OCE(cmt)`
`=>OD=OE` ( `2` cạnh tương ứng )
Có `CD ⊥ AB(GT)=>hat(ADC)=90^0=>hat(ADO)=90^0`
`BE⊥AC(GT)=>hat(AEB)=90^0=>hat(AEO)=90^0`
Xét `Delta ADO` và `Delta AEO` có :
`hat(ADO)=hat(AEO)(=90^0)`
`AO` -chung
`DO=EO(cmt)`
`=>Delta ADO=Delta AEO(c.h-c.g.v)`
`=>AD=AE` ( hai cạnh tương ứng )
`=>Delta ADE` cân tại `A=>hat(ADE)=(180^0-hat(A))/2`
`Delta ABC` cân tại `A(AB=AC)=>hat(ABC)=(180^0-hat(A))/2`
nên `hat(ADE)=hat(ABC)`
mà `2` góc này ở vị trí đvị
nên `DE////BC`(đpcm)
hình :
Bài 1: Cho tam giác ABC nhọn; vẽ về phía ngoài tam giác ABC các tam giác vuông cân tại A là tam giác ABD và tam giác ACE
a) Chứng minh DC=BE và DC\(\perp\)BE
b) Gọi H là chân đường vuông góc kẻ từ A đến ED và M là trung điểm của đoạn thẳng BC. Chứng minh A,M,H thẳng hàng
a) ta có EAB=\(90^0+BAC\)
DAC=\(90^0+BAC\)
=> EAB=DAC
XÉT \(\Delta EAB\)VÀ \(\Delta CAD\)
AE=AC
AD=AB
EAB=DAC
\(\Rightarrow\Delta EAB=\Delta CAD\left(c-g-c\right)\)
\(\Rightarrow BE=DC\)(CẠNH TƯƠNG ỨNG)
Cho tam giác .ABC cân tại A. Kẻ BH | AC; CK perp AB ( H in AC ; K in AB ). a) Chứng minh tam giác AKH là tam giác cản b) Gọi I là giao của BH và CK; A cắt BC tại M. Chứng minh rằng IM là phân giác của hat BIC c) Chứng minh. HK //BC
a: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
góc HAB chung
=>ΔAHB=ΔAKC
=>AH=AK
b: Xét ΔKBC vuông tại K và ΔHCB vuông tại H có
BC chung
góc KBC=góc HCB
=>ΔKBC=ΔHCB
=>góc IBC=góc ICB
=>ΔIBC can tại I
Xét ΔABC có
BH,CK là đường cao
BH cắt CK tại I
=>I là trực tâm
=>AI vuông góc BC tại M
ΔIBC cân tại I
mà IM là đường cao
nên IM là phân giác của góc BIC
c: Xét ΔABC có AK/AB=AH/AC
nên KH//BC
Bài 1: Cho ABC cân tại A có A <90 độ Vẽ BE ⊥AC tại E và CD ⊥ AB tại D. a) Chứng minh BC=CD và tam giác ADE cân tại A. b) Gọi H là giao điểm của BE và CD. Chứng minh AH là tia phân giác của BAC c) Chimg minh DE//BC. d) Gọi M là trung điểm cạnh BC. Chứng minh ba điểm A,H,M thẳng hàng.Bài 2: Cho ABC vuông tại B. AD là tin phân giác của BAC (D ∈ BC).Kẻ DI ⊥ AC(I ∈ AC) a) Chứng minh tam giác ABD=tam giác AID b) So sánh DB và DC. c) Từ C kẻ đường thẳng vuông góc với AD, cắt AD tại K. Hai đường thẳng CK và AB cắt nhau tại E. Chứng minh K là trung điểm của CE và tam giác AEC cân d) Chứng minh BI // EC. e) Chứng minh ba điểm E. D. I thẳng hàng BÀI 3. Cho tam giác ABC cân tại A. Gọi M là trung điểm của AC. Trên tia đối của tia MB lấy điểm D sao cho DM – BM a. Chứng minh tam giác BMC = tam giác DMA. Suy ra AD//BC b. Chứng minh tam giác ACD là tam giác cân c. Trên tia đối của tia CA lấy điểm E sao cho CA = CE. Chứng minh DC đi qua trung điểm I của BE Bài 4. Cho tam giác ABC cân tại A, đường phân giác AH a) Chứng minh tam giác ABH bằng tam giác ACH b Chứng minh AH là đường trung tuyến ABC. Bài 5. Cho tam giác .07C cân tại A có ABC = 70. Kẻ BD ⊥C(D∈AC), C⊥(E∈AB) và BD, CE cắt nhau tại H. a) Tính số do các góc còn lại của tam giác ABC. b) Chứng minh BD = CE c) Chứng minh tia AH là tia phân giác của góc BAC .
Cho tam giác ABC vuông tại A có AC>AB. Đường cao AH. Từ H kẻ HD\(\perp\)AB (D\(\in\)AB), HE\(\perp\)AC( E\(\in\)AC).
a. Chứng minh: \(\Delta AED\sim\Delta ABC\)
b. Gọi M là điểm đối xứng của B qua H. Từ M kẻ đường thẳng vuông góc với BC cắt cạnh AC tại N. Chứng minh rằng DE song song với BN
d.Chứng minh rằng: \(\dfrac{AB^3}{AC^3}=\dfrac{BD}{CE}\)
---> Giúp minh với ạ, mai mình nộp rồiT.T
Sau gần một buổi trưa lăn lội với Thales, đồng dạng ở câu b thì t đã nghĩ đến cách của lớp 7 ~ ai dè làm được ^^
Sao bổ sung hình vẽ không được vậy nè
Cho tam giác vuông ABC, \(\widehat{A}=90^o\), \(AH\perp BC\) tại H. \(HD\perp AC\) tại D và \(HE\perp AB\) tại E. M là trung điểm của HC
a) Chứng minh tứ giác AEHD là HCN
b) N là trung điểm của AE, O là giao điểm của AH và DE. Chứng minh M, O, N thẳng hàng
c) Chứng minh \(\Delta MDE\) là tam giác vuông
(answer hết mk sẽ đánh dấu like)
a: Xét tứ giác AEHD có
\(\widehat{AEH}=\widehat{ADH}=\widehat{DAE}=90^0\)
Do đó: AEHD là hình chữ nhật