Chứng minh rằng
1 - 1/4sin2x + cosx = cos4(x/2) + cos2(x/2)
Những câu hỏi liên quan
Chứng minh các đẳng thức sau:
1/ \(sin^6\alpha+cos^6\alpha=\frac{5}{8}+\frac{3}{8}cos4\alpha\)
2/\(\frac{1+sin2\alpha-cos2\alpha}{1+cos2\alpha}=tan\alpha+tan^2\alpha\)
\(sin^6a+cos^6a=\left(sin^2x\right)^3+\left(cos^2x\right)^3\)
\(=\left(sin^2x+cos^2x\right)\left(sin^4x+cos^4x-sin^2x.cos^2x\right)\)
\(=sin^4x+2sin^2xcos^2x+cos^4x-3sin^2x.cos^2x\)
\(=\left(sin^2x+cos^2x\right)^2-\frac{3}{4}.\left(2sinx.cosx\right)^2\)
\(=1-\frac{3}{4}sin^22x=1-\frac{3}{4}\left(\frac{1}{2}-\frac{1}{2}cos4x\right)=\frac{5}{8}+\frac{3}{8}cos4x\)
2/
\(\frac{1+sin2a-cos2a}{1+cos2a}=\frac{1+2sina.cosa-\left(1-2sin^2a\right)}{1+2cos^2a-1}=\frac{2sina.cosa+2sin^2a}{2cos^2a}\)
\(=\frac{2sina.cosa}{2cos^2a}+\frac{2sin^2a}{2cos^2a}=tana+tan^2a\)
Đúng 0
Bình luận (1)
Câu 1 : Chứng minh rằng : 3 - 4sin2x = 4cos2x - 1Câu 2 : Chứng minh rằng : cos4x - sin4x = 2cos2x - 1 = 1 - 2sin2xCâu 3 : Chứng minh rằng : sin4x + cos4x = 1 - 2sin2xCos2x
1/ \(3-4\sin^2=4\cos^2x-1\Leftrightarrow4\left(\sin^2x+\cos^2x\right)-4=0\Leftrightarrow4.1-4=0\left(ld\right)\Rightarrow dpcm\)
2/ \(\cos^4x-\sin^4x=\left(\cos^2x+\sin^2x\right)\left(\cos^2x-\sin^2x\right)=\cos^2x-\left(1-\cos^2x\right)=2\cos^2x-1=\left(1-\sin^2x\right)-\sin^2x=1-2\sin^2x\)
3/ \(\sin^4x+\cos^4x=\left(\sin^2x+\cos^2x\right)^2-2\sin^2x.\cos^2x=1-2\sin^2x.\cos^2x\)
Đúng 2
Bình luận (0)
Cho cot a 2. Tính giá trị của biểu thức
P
sin
4
a
+
cos
4
x
sin
2
a
+
cos
2
x
. Giá trị của P là A.
P...
Đọc tiếp
Cho cot a = 2. Tính giá trị của biểu thức P = sin 4 a + cos 4 x sin 2 a + cos 2 x . Giá trị của P là
A. P = - 17 25
B. P = - 27 15
C. P = - 17 15
D. P = 17 15
giải các phương trình sau : a). sin 2x+sin2 x=1/2
b.2sin2 x +3 sin x cosx + cos2 x= 0
c.sin2 x/2 + sin x - 2 cos 2 x/2 = 1/2
Số các giá trị thực của tham số m để phương trình (sin x-1)(2cos^2 x - (sinx -1)(2
cos
2
x
–(2m+1)cosx+m)0 có đúng 4 nghiệm thực thuộc đoạn
0
;
2
π
là A. 1. B. 2. C. 3. D. Vô số.
Đọc tiếp
Số các giá trị thực của tham số m để phương trình (sin x-1)(2cos^2 x - (sinx -1)(2 cos 2 x –(2m+1)cosx+m)=0 có đúng 4 nghiệm thực thuộc đoạn 0 ; 2 π là
A. 1.
B. 2.
C. 3.
D. Vô số.
Đáp án B.
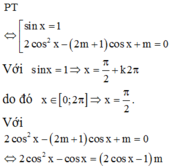
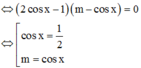
PT: cos x = 1 2 có 2 nghiệm thuộc trên đoạn 0 ; 2 π do đó để PT đã cho có 4 nghiệm thực thuộc đoạn 0 ; 2 π thì
TH1: m= cosx có 1 nghiệm thuộc đoạn 0 ; 2 π
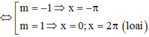
TH2: m= cosx có 2 nghiệm thuộc đoạn 0 ; 2 π trong đó có 1 nghiệm trùng
Vậy m= -1; m=0.
Đúng 0
Bình luận (0)
chứng minh: cosx/sinx-cosx + sinx/sinx+cosx=1+cot2x/1-cot2x
Giải pt đối xứng 1)2sinxcosx-12sinx+12cosx=-12 2)|sinx-cosx|+4sin2x=1
Rút gọn biểu thức : A frac{tanalpha-cotalpha}{tanalpha+cotalpha}+cos2alpha
Bfrac{1+sin4alpha-cos4alpha}{1+sin4alpha+cos4alpha}
Cfrac{3-4cos2alpha+cos4alpha}{3+4cos2alpha+cos4alpha}
Dfrac{sin^22alpha+4sin^4alpha-4sin^2alpha.cos^2alpha}{4-sin^22alpha-4sin^2alpha}
Đọc tiếp
Rút gọn biểu thức : A = \(\frac{tan\alpha-cot\alpha}{tan\alpha+cot\alpha}+cos2\alpha\)
\(B=\frac{1+sin4\alpha-cos4\alpha}{1+sin4\alpha+cos4\alpha}\)
\(C=\frac{3-4cos2\alpha+cos4\alpha}{3+4cos2\alpha+cos4\alpha}\)
\(D=\frac{sin^22\alpha+4sin^4\alpha-4sin^2\alpha.cos^2\alpha}{4-sin^22\alpha-4sin^2\alpha}\)
Nhân cả tử và mẫu của phân số chứa tan với \(sina.cosa\)
\(A=\frac{sin^2x-cos^2x}{sin^2x+cos^2x}+cos2x=sin^2x-cos^2x+cos2x=-cos2x+cos2x=0\)
\(B=\frac{1+sin4a-cos4a}{1+sin4a+cos4a}=\frac{1+2sin2a.cos2a-\left(1-2sin^22a\right)}{1+2sin4a.cos4a+2cos^22a-1}\)
\(B=\frac{2sin2a\left(sin2a+cos2a\right)}{2cos2a\left(sin2a+cos2a\right)}=\frac{sin2a}{cos2a}=tan2a\)
\(C=\frac{3-4cos2a+2cos^22a-1}{3+4cos2a+2cos^22a-1}=\frac{2\left(cos^22a-2cos2a-1\right)}{2\left(cos^22a+2cos2a+1\right)}\)
\(C=\frac{\left(cos2a-1\right)^2}{\left(cos2a+1\right)^2}=\frac{\left(1-2sin^2a-1\right)^2}{\left(2cos^2a-1+1\right)^2}=\frac{sin^4a}{cos^4a}=tan^4a\)
\(D=\frac{sin^22a+4sin^4a-\left(2sina.cosa\right)^2}{4-4sin^2a-sin^22a}=\frac{sin^22a+4sin^4a-sin^22a}{4\left(1-sin^2a\right)-\left(2sina.cosa\right)^2}=\frac{4sin^4a}{4cos^2a-4sin^2a.cos^2a}\)
\(=\frac{sin^4a}{cos^2a\left(1-sin^2a\right)}=\frac{sin^4a}{cos^2a.cos^2a}=\frac{sin^4a}{cos^4a}=tan^4a\)
Đúng 0
Bình luận (0)
1. Chứng minh rằng: \(\frac{1-cosx+cos2x}{sin2x-sinx}=cotx\)
2. Chứng minh biểu thức sau không phụ thuộc \(x\): \(A=sin\left(\frac{\pi}{4}+x\right)-cos\left(\frac{\pi}{4}-x\right)\), nếu \(cosx=\frac{1}{2}\) với \(\frac{3\pi}{2}< x< 2\pi\)
\(\frac{1-cosx+cos2x}{sin2x-sinx}=\frac{1-cosx+2cos^2x-1}{2sinx.cosx-sinx}=\frac{cosx\left(2cosx-1\right)}{sinx\left(2cosx-1\right)}=\frac{cosx}{sinx}=cotx\)
\(A=sin\left(\frac{\pi}{4}+x\right)-sin\left(\frac{\pi}{2}-\frac{\pi}{4}+x\right)=sin\left(\frac{\pi}{4}+x\right)-sin\left(\frac{\pi}{4}+x\right)=0\)
Đúng 0
Bình luận (0)