Tìm tất cả các giá trị thực m để phương trình x+1=\(\sqrt[m]{2x^2+1}\) có hai nghiệm phân biệt
Cho phương trình \(\sqrt{2x+m}=x-1\). Tất cả các giá trị của m để phương trình có hai nghiệm phân biệt lớn hơn 1
Xét với \(x>1\)
\(\sqrt{2x+m}=x-1\)
\(\Leftrightarrow2x+m=x^2-2x+1\)
\(\Leftrightarrow x^2-4x+1=m\)
Xét hàm \(f\left(x\right)=x^2-4x+1\) với \(x>1\)
\(-\dfrac{b}{2a}=2\) ; \(f\left(1\right)=-2\) ; \(f\left(2\right)=-3\)
\(\Rightarrow\) Pt có 2 nghiệm pb lớn hơn 1 khi \(-3< m< -2\)
Câu 1: Tìm tất cả các giá trị cuả tham số m để phương trình \(4\sqrt{x^2-4x+5} =x^2-4x+2m-1\) có 4 nghiệm phân biệt
Câu 2: Tìm các giá trị của tham số m sao cho tổng các bình phương hai nghiệm của phương trình \((m-3)x^2+2x-4=0\) bằng 4
Câu 3: Cho tam giác ABC có \(BC=a, AC=b, AB=c\) và I là tâm đường tròn nội tiếp tam giác. Chứng minh rằng: \(a\overrightarrow{IA}+b\overrightarrow{IB}+c\overrightarrow{IC}=\overrightarrow{0}\)
Câu 4: Cho tam giác ABC. Gọi D,I lần lượt là các điểm xác định bởi \(3\overrightarrow{BD}-\overrightarrow{BC}=\overrightarrow{0}\) và \(\overrightarrow{IA}+\overrightarrow{ID}=\overrightarrow{0}\). Gọi M là điểm thỏa mãn \(\overrightarrow{AM}=x\overrightarrow{AC}\) (x∈R)
a) Biểu thị \(\overrightarrow{BI}\) theo \(\overrightarrow{BA}\) và \(\overrightarrow{BC}\)
b) Tìm x để ba điểm B,I,M thẳng hàng
1.
Đặt \(\sqrt{x^2-4x+5}=t\ge1\Rightarrow x^2-4x=t^2-5\)
Pt trở thành:
\(4t=t^2-5+2m-1\)
\(\Leftrightarrow t^2-4t+2m-6=0\) (1)
Pt đã cho có 4 nghiệm pb khi và chỉ khi (1) có 2 nghiệm pb đều lớn hơn 1
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'=4-\left(2m-6\right)>0\\\left(t_1-1\right)\left(t_2-1\right)>0\\\dfrac{t_1+t_2}{2}>1\\\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}10-2m>0\\t_1t_2-\left(t_1+t_1\right)+1>0\\t_1+t_2>2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< 5\\2m-6-4+1>0\\4>2\end{matrix}\right.\) \(\Leftrightarrow\dfrac{9}{2}< m< 5\)
2.
Để pt đã cho có 2 nghiệm:
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne3\\\Delta'=1+4\left(m-3\right)\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne3\\m\ge\dfrac{11}{4}\end{matrix}\right.\)
Khi đó:
\(x_1^2+x_2^2=4\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=4\)
\(\Leftrightarrow\dfrac{4}{\left(m-3\right)^2}+\dfrac{8}{m-3}=4\)
\(\Leftrightarrow\dfrac{1}{\left(m-3\right)^2}+\dfrac{2}{m-3}-1=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{1}{m-3}=-1-\sqrt{2}\\\dfrac{1}{m-3}=-1+\sqrt{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m=4-\sqrt{2}< \dfrac{11}{4}\left(loại\right)\\m=4+\sqrt{2}\end{matrix}\right.\)
3.
Nối AI kéo dài cắt BC tại D thì D là chân đường vuông góc của đỉnh A trên BC
\(\Rightarrow\dfrac{DB}{DC}=\dfrac{AB}{AC}=\dfrac{c}{b}\)
\(\Rightarrow\overrightarrow{BD}=\dfrac{c}{b}\overrightarrow{DC}\)
\(\Leftrightarrow\overrightarrow{ID}-\overrightarrow{IB}=\dfrac{c}{b}\left(\overrightarrow{IC}-\overrightarrow{ID}\right)\)
\(\Leftrightarrow b.\overrightarrow{IB}+\overrightarrow{c}.\overrightarrow{IC}=\left(b+c\right)\overrightarrow{ID}\) (1)
Mặt khác:
\(\dfrac{ID}{IA}=\dfrac{BD}{AB}=\dfrac{CD}{AC}=\dfrac{BD+CD}{AB+AC}=\dfrac{BC}{AB+AC}=\dfrac{a}{b+c}\)
\(\Leftrightarrow\left(b+c\right)\overrightarrow{ID}=-a.\overrightarrow{IA}\) (2)
(1); (2) \(\Rightarrow a.\overrightarrow{IA}+b.\overrightarrow{IB}+c.\overrightarrow{IC}=\left(b+c\right)\overrightarrow{ID}-\left(b+c\right)\overrightarrow{ID}=\overrightarrow{0}\)
Tìm tất cả các giá trị thực của m để phương trình x + 1 = m 2 x 2 + 1 có hai nghiệm phân biệt?
A. - 2 2 < m < 6 6
B. m < 2 2
D. m > 6 6
D. 2 2 < m < 6 6
Đáp án D
Phương trình x + 1 = m 2 x 2 + 1 ⇔ m = x + 1 2 x 2 + 1 ; ∀ x ∈ ℝ
Xét hàm số f x = x + 1 2 x 2 + 1 trên ℝ có f ' x = 1 - 2 x 2 x 2 + 1 3 = 0 ⇔ x = 1 2 .
Tính các giá trị f 1 2 = 6 2 ; lim x → + ∞ f x = 1 2 ; lim x → - ∞ f x = - 1 2
Khi đó, để f(x) = m có 2 nghiệm phân biệt ⇔ 2 2 < m < 6 6 .
Hình bên là đồ thị của hàm số y = 2 x + 1 x - 1 Tìm tất cả các giá trị thực của tham số m để phương trình 2 x + 1 | x - 1 | = m có hai nghiệm phân biệt.
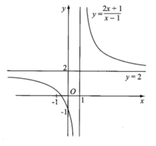
A. m > 2
B. Không có giá trị của m.
C. m > -2
D. Với mọi m.
Tìm tất cả các giá trị thực của tham số m để phương trình x . log 2 x − 1 + m = m . log 2 x − 1 + x có hai nghiệm thực phân biệt.
A. m > 1 v à m ≠ 2
B. m ≠ 3
C. m > 1 v à m ≠ 3
D. m > 1
Đáp án C
Ta có: x . log 2 x − 1 + m = m . log 2 x − 1 + x
⇔ x − m . log 2 x − 1 = x − m .
⇔ x − m log 2 x − 1 − 1 ⇔ x − m = 0 log 2 x − 1 = 1 ⇔ x = m x − 1 = 2 ⇔ x = m x = 3 *
Để phương trình đã cho có 2 nghiệm phân biệt ⇔ * có nghiệm duy nhất x > 1 ; x ≠ 3. Vậy m > 1 v à m ≠ 3 là giá trị cần tìm.
tìm tất cả các giá trị của tham số m để phương trình sau √x^2 + 2x +3m = 2x+1 có hai nghiệm phân biệt
\(PT\Leftrightarrow x^2+2x+3x=4x^2+4x+1\\ \Leftrightarrow3x^2+2x+1-3m=0\\ \text{PT có 2 nghiệm pb}\Leftrightarrow\Delta'>0\\ \Leftrightarrow1-3\left(1-3m\right)>0\\ \Leftrightarrow1+9m-1>0\Leftrightarrow m>0\)
tìm tất cả các giá trị của tham số m để phương trình sau √x^2 + 2x +3m = 2x+1 có hai nghiệm phân biệt
\(PT\Leftrightarrow x^2+2x+3m=4x^2+4x+1\\ \Leftrightarrow3x^2+2x+1-3m=0\)
PT có 2 nghiệm phân biệt \(\Leftrightarrow\Delta'=1-3\left(1-3m\right)>0\)
\(\Leftrightarrow9m-2>0\\ \Leftrightarrow m>\dfrac{2}{9}\)
Vậy PT có 2 nghiệm pb \(\Leftrightarrow m>\dfrac{2}{9}\)
Hình bên là đồ thị hàm số y = 2 x + 1 x - 1 Tìm tất cả các giá trị thực của tham số m để phương trình | 2 x + 1 | | x - 1 | = 2 m có hai nghiệm phân biệt
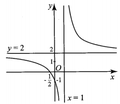
A.Với mọi m
B. Không có giá trị của m
C.![]()
D. ![]()
Đáp án D
Từ đồ thị đã cho ta suy ra đồ thị hàm số ![]()
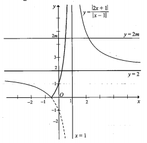
Từ đó ta có kết quả thỏa mãn yêu cầu bài toán là ![]()
Hình vẽ dưới đây là đồ thị của hàm số y = 3 x - 2 x - 1 . Tìm tất cả các giá trị thực của tham số m để phương trình 3 x - 2 x - 1 = m có hai nghiệm phân biệt?
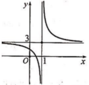
A. -3 < m < 0
B. m < -3
C. 0 < m < 3
D. m > 3
Tìm tất cả các giá trị thực của m để phương trình \(4^x-2^{x+1}+m=0\) có 2 nghiệm thực phân biệt
Đặt \(t=2^x>0\).
Phương trình ban đầu trở thành: \(t^2-2t+m=0\) (*)
Để phương trình ban đầu có 2 nghiệm phân biệt thì (*) phải có 2 nghiệm phân biệt dương: \(\left\{{}\begin{matrix}\Delta'>0\\t_1+t_2>0\\t_1t_2>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}1-m>0\\2>0\left(đúng\right)\\m>0\end{matrix}\right.\Leftrightarrow0< m< 1\)