a -3      b - 4      c - 1      d - 2

Chọn B

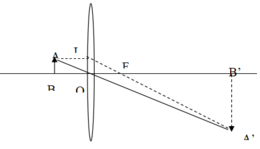
DOBA đồng dạng với DOB’A’

AB/A’B’=OB/OB’=> 1/3=30/OB’=>OB’=90cm

DOIF đồng dạng với DB’A’F

OF/B’F=AB/3AB=1/3=> OF=1/3B’F

OF+B’F=OB’=> 4OF=90=>OF=20,5cm

Tiêu cự là 22,5 cm

Chọn đáp án D

+ Với thấu kính hội tụ, khi vật nằm trong khoảng 0 < f < d →  Ảnh ảo cùng chiều và lớn hơn vật

a)Thấu kính hội tụ cho ảnh A'B' là ảnh thật.

Ảnh A'B' ngược chiều vật và nhỏ hơn vật.

b)Khoảng cách từ ảnh đến thấu kính:

\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow\dfrac{1}{30}=\dfrac{1}{45}+\dfrac{1}{d'}\)

\(\Rightarrow d'=90cm\)

Chiều cao ảnh:

\(\dfrac{h}{h'}=\dfrac{d}{d'}\Rightarrow\dfrac{15}{h'}=\dfrac{45}{90}\)

\(\Rightarrow h'=A'B'=30cm\)

Ảnh A’B’ của AB qua thấu kính là ảnh thật, ngược chiều và lớn bằng vật.

→ Đáp án D

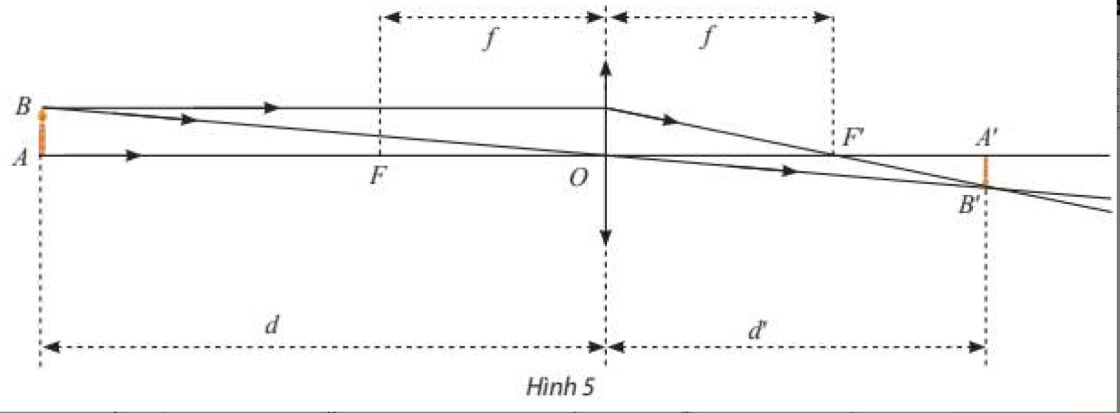
a) \(\mathop {\lim }\limits_{d \to {f^ + }} g\left( d \right) = \mathop {\lim }\limits_{d \to {f^ + }} \frac{{df}}{{d - f}} = \mathop {\lim }\limits_{d \to {f^ + }} \left( {df} \right).\mathop {\lim }\limits_{d \to {f^ + }} \frac{1}{{d - f}}\)

Ta có: \(\mathop {\lim }\limits_{d \to {f^ + }} \left( {df} \right) = f\mathop {\lim }\limits_{d \to {f^ + }} d = {f^2};\mathop {\lim }\limits_{d \to {f^ + }} \frac{1}{{d - f}} =  + \infty \)

\( \Rightarrow \mathop {\lim }\limits_{d \to {f^ + }} g\left( d \right) = \mathop {\lim }\limits_{d \to {f^ + }} \frac{{df}}{{d - f}} =  + \infty \)

Ý nghĩa: Khi vật dần đến tiêu điểm từ phía xa thấu kính đến gần thấu kính thì khoảng cách từ ảnh đến thấu kính dần đến \( + \infty \).

b) \(\mathop {\lim }\limits_{d \to  + \infty } g\left( d \right) = \mathop {\lim }\limits_{d \to  + \infty } \frac{{df}}{{d - f}} = \mathop {\lim }\limits_{d \to  + \infty } \frac{{df}}{{d\left( {1 - \frac{f}{d}} \right)}} = \mathop {\lim }\limits_{d \to  + \infty } \frac{f}{{1 - \frac{f}{d}}} = \frac{f}{{1 - 0}} = f\)

Ý nghĩa: Khi khoảng cách từ vật đến thấu kính càng xa thì ảnh tiến dần đến tiêu điểm của ảnh \(\left( {F'} \right)\).

Đáp án B

f = 22,5cm

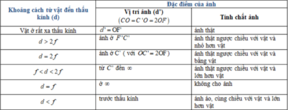
=> Khi đặt vật AB vuông góc với trục chính của thấu kính hội và cách thấu kính một khoảng d > 2f thì ảnh A’B’ của AB qua thấu kính là ảnh thật ngược chiều với vật và nhỏ hơn vật

Đáp án: A