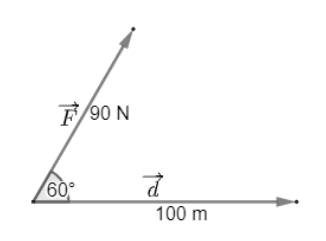
Công sinh bởi lực \(\overrightarrow F \) được tính bằng công thức

\(A = \overrightarrow F .\overrightarrow d  = \left| {\overrightarrow F } \right|.\left| {\overrightarrow d } \right|.\cos \left( {\overrightarrow F ,\overrightarrow d } \right) = 90.100.\cos 60^\circ  = 4500\) (J)

Vậy công sinh bởi lực \(\overrightarrow F \) có độ lớn bằng 4500 (J)

Gọi vectơ dịch chuyển của vật là \(\overrightarrow d \), ta có \(|\overrightarrow d |\; = 50\).

Theo giả thiết \(\overrightarrow F \) và \(\overrightarrow d \) cùng hướng nên \(\left( {\overrightarrow F ,\overrightarrow d } \right) = 0^\circ \)

Công sinh ra bởi lực \(\overrightarrow F \)được tính bằng:

\(A = \overrightarrow F .\overrightarrow d  = \left| {\overrightarrow F } \right|.\left| {\overrightarrow d } \right|.\cos \left( {\overrightarrow F ,\overrightarrow d } \right) = 20.50.\cos 0^\circ  = 1000\) (J)

Theo đinh lý Pytago: \(\left(30\sqrt{2}\cdot cos45^o\right)-20=10m\)

Về phía Nam.

Chọn C.

Quãng đường đi về phía Bắc là:
     60\(.\dfrac{1}{4}\)=15km
Độ dịch chuyển là
\(\sqrt{5^2+15^2}\) =15,8 km

Tóm tắt:
V₁ = 2 m/s
S₁ = 2,2 km
t₁ = ?
V₂ = 60 km/h = \(\dfrac{50}{3}\) m/s
t₂ = 15 min = 900 s
S₂ = ?
S_tổng = ?
t_tổng = ?
V_tb = ?
v = ?
                                Giải
a) Quãng đường người đó đi được về hướng Bắc là:
\(S_2=v_2 . t_2=\dfrac{50}{3} . 900=15000\left(m\right)\) 
Tổng quãng đường mà người đó đã đi là:
\(S_{tổng}=S_1+S_2=2200+15000=17200\left(m\right)\) 
b) Từ tóm tắt ta có thể vẽ ra một hình như sau:
 
Từ hình vẽ, chúng ta có thể xác định được rằng là:
Độ dịch chuyển tổng hợp chính là cạnh huyền của tam giác
\(\text{Δ }d=\sqrt{S^2_1+S^2_2}=\sqrt{2200^2+15000^2}\approx15160,5\left(m\right)\) 
c) Thời gian người này đi được ở quãng đường thứ nhất là:
\(t_1=\dfrac{S_1}{v_1}=\dfrac{2200}{2}=1100\) (s)
Tổng thời gian người này đi được trên cả hai quãng đường là:
\(t_{tổng}=t_1+t_2=1100+900=2000\) (s)
d) Tốc độ trung bình của người đó trên cả hai quãng đường là:
\(V_{tb}=\dfrac{S_1+S_2}{t_1+t_2}=\dfrac{2200+15000}{1100+900}=8,6\) (m/s)
e) Độ lớn của vận tốc trung bình là:
\(v=\dfrac{\text{Δ }d}{t}=\dfrac{15160,5}{2000}=7,58\) (m/s)
 

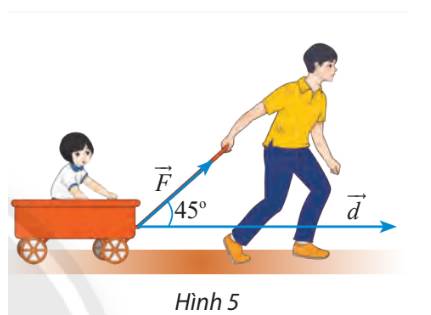
Theo giả thiết ta có: \(A = \left| {\overrightarrow F } \right|.\left| {\overrightarrow d } \right|.\cos \left( {\overrightarrow F ,\overrightarrow d } \right)\)

\( \Rightarrow A = 10.100.\cos 45^\circ  = 500\sqrt 2 \left( J \right)\)

Vậy công sinh bởi lực \(\overrightarrow F \) là \(500\sqrt 2 \) (J)

Ta thấy rô bốt đi từ A đến B, sau đó đi từ B đến C, vậy cả 2 lần di chuyển thì ta thấy điểm cuất phát là A và điểm kết thúc là C.

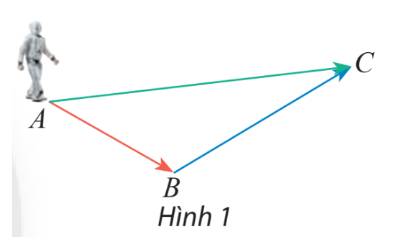
Suy ra vectơ biểu diễn sự dịch chuyển của rô bốt sau hai lần dịch chuyển là vectơ \(\overrightarrow {AC} \)

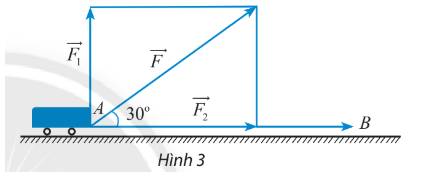
Ta xác định được các độ lớn:

\(\left| {\overrightarrow F } \right| = 50,\left| {\overrightarrow {{F_2}} } \right| = \left| {\overrightarrow F } \right|\cos 30^\circ  = 50.\frac{{\sqrt 3 }}{2} = 25\sqrt 3 ,\left| {\overrightarrow {{F_1}} } \right| = \left| {\overrightarrow F } \right|.\sin 30^\circ  = 50.\frac{1}{2} = 25\) (N)

Dựa vào hình vẽ ta có: \(\left( {\overrightarrow F ,\overrightarrow d } \right) = 30^\circ ,\left( {\overrightarrow {{F_1}} ,\overrightarrow d } \right) = 90^\circ ,\left( {\overrightarrow {{F_2}} ,\overrightarrow d } \right) = 0^\circ \)

Áp dụng công thức tính công sinh ra bởi lực \(A = \overrightarrow F .\overrightarrow d \) ta có:

\(A = \overrightarrow F .\overrightarrow d  = \left| {\overrightarrow F } \right|\left| {\overrightarrow d } \right|\cos \left( {\overrightarrow F ,\overrightarrow d } \right) = 50.200.\cos 30^\circ  = 5000 (J)\)

\({A_1} = \overrightarrow {{F_1}} .\overrightarrow d  = \left| {\overrightarrow {{F_1}} } \right|\left| {\overrightarrow d } \right|\cos \left( {\overrightarrow {{F_1}} ,\overrightarrow d } \right) = 25.200.\cos 90^\circ  = 0 (J)\)

\({A_2} = \overrightarrow {{F_2}} .\overrightarrow d  = \left| {\overrightarrow {{F_2}} } \right|\left| {\overrightarrow d } \right|\cos \left( {\overrightarrow {{F_2}} ,\overrightarrow d } \right) = 25\sqrt 3 .200.\cos 0^\circ  = 5000\sqrt 3  (J)\)

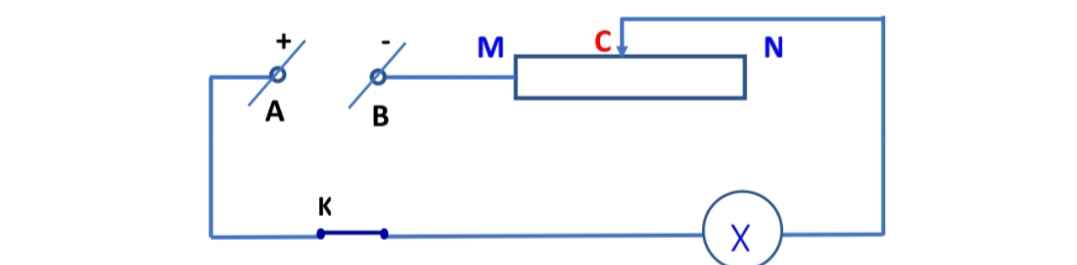
a)\(C\equiv B\)\(\Rightarrow R_{tđ}max\)

              \(\Leftrightarrow Imin\)(U không đổi)

              \(\Rightarrow\) \(I_Đ\) nhỏ nhất

              \(\Rightarrow\) Đèn sáng yếu nhất.

b)Ngược lại câu a.