Cho hai đường d1 và d2 có phương trình:
d1: 2x - 6y = 10
d2: x + ky=4 (k#0)
a) Tính giá trị của k để d1// d2
b) Tìm giá trị cuả k để hai đường thẳng cóa điểm chung là A(-1;-2)
Những câu hỏi liên quan
1.Phân tích
(a - x)^2 + (a/2)^2
2. Cho hai đg thẳng d1 và d2 có phương trình:
d1 : 2x -6y =10
d2: x + ky =4
a) Tính giá trị của k để d1 // d2
b) Tìm giá trị của k để hai đường thẳng có điểm chung là A( -1;-2)
Bài 2:
a: Để hai đường song song thì 2/1=-6/k<>10/4
=>-6/k=2
=>k=-3
b: Thay x=-1 và y=-2 vào (d2), ta được:
-1-2k=4
=>2k=-5
=>k=-5/2
Đúng 0
Bình luận (0)
Cho hai đg thẳng d1 , d2 có pt:
d1 : 2x - 6y = 10
d2 : x + ky = 4 (k # 0)
a) Tính giá trị của k để d1// d2
b) Tìm giá trị của k để 2 đg thẲNG có điểm chung là A(-1;-2)
a) d1//d2 khi và chỉ khi \(\dfrac{2}{1}=-\dfrac{6}{k}\Rightarrow k=-3\)
b) thay tọa độ A(-1;-2) vào PT d1 ta được: 2(-1)-6(-2)=10 (đúng)
=> A thuộc d1.
=> hai đường thẳng có điểm chung là A <=> A thuộc d2
thay tọa độ A(-1;-2) vào PT d2 ta được: -1+k(-2)=4<=>k=-5/2
Đúng 0
Bình luận (0)
trong mặt phẳng tọa độ Oxy,cho hai đường thẳng d1:2x-y+5=0,d2:3x+6y-1=0 và điểm P(-2,0).Gọi A là giao điểm của d1 và d2.Khi đó đường thẳng d đi qua P và cùng với d1,d2 tạo thành một tam giác cân đỉnh A có phương trình là?
Gọi \(M\left(x;y\right)\) là điểm cách đều \(d_1\) và \(d_2\)
\(\Rightarrow\dfrac{\left|2x-y+5\right|}{\sqrt{2^2+\left(-1\right)^2}}=\dfrac{\left|3x+6y-1\right|}{\sqrt{3^2+6^2}}\)
\(\Leftrightarrow\left|6x-3y+15\right|=\left|3x+6y-1\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-9y+16=0\\9x+3y+14=0\end{matrix}\right.\)
\(\Rightarrow\) Phương trình đường thẳng cần tìm có dạng:
\(\left[{}\begin{matrix}9\left(x+2\right)+3\left(y-0\right)=0\\3\left(x+2\right)-9\left(y-0\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}3x+y+6=0\\x-3y+2=0\end{matrix}\right.\)
Có 2 đường thẳng thỏa mãn
Đúng 1
Bình luận (0)
Phương trình đường thẳng d1: y(m+1)x +3n+1, m-1 phương trình đường thẳng d2: yx+4 và d3: y2x+4. Để đường thẳng d1, d2 và d3 đồng quy và d1 cắt hai trục tọa độ tạo tam giác có diện tích bằng 4 thì giá trị m+n là A. 2 B. 1 C. 5 D. 6
Đọc tiếp
Phương trình đường thẳng d1: y=(m+1)x +3n+1, m>-1 phương trình đường thẳng d2: y=x+4 và d3: y=2x+4. Để đường thẳng d1, d2 và d3 đồng quy và d1 cắt hai trục tọa độ tạo tam giác có diện tích bằng 4 thì giá trị m+n là
A. 2
B. 1
C. 5
D. 6
Trong mặt phẳng Oxy cho 2 đường thẳng d1: 2x - y + 5=0, d2: 3x + 6y - 7=0. Lập phương trình đường thẳng đi qua P (2; -1) sao cho đường thẳng đó cắt d1, d2 tạo ra một tam giác cân có đỉnh là giao điểm của d1, d2
d1 có 1 vtpt là \(\overrightarrow{n1}\)(2;-1);d2 có 1 vtpt là \(\overrightarrow{n2}\)(3;6)
Ta có \(\overrightarrow{n1}\)\(\times\)\(\overrightarrow{n2}\)=2\(\times\)3-1\(\times\)6=0 nên d1 vuông góc d2 và d1 cắt d2 tại I(I khác P)
Gọi d là đườg thẳng đi qua P;d:A(x-2)+B(y+1)=0\(\Leftrightarrow\)Ax+By-2A+B=0
d cắt d1;d2 tạo thành một tam giác cân có đỉnh I\(\Leftrightarrow\)d tạo với d1(hoặc d2) một góc 45
\(\Leftrightarrow\)\(\frac{\left|2A-B\right|}{\sqrt{A^2+B^2}\sqrt{2^2+\left(-1\right)^2}}\)=\(\cos45\)
\(\Leftrightarrow\)\(3A^2\)-8AB-\(3B^2\)=0
\(\Leftrightarrow\)A=3B hoặc B=-3A
Nếu A=3B ta có d:3x+y-5=0
Nếu B=-3A to có d:x-3y-5=0
Vậy......
Đúng 0
Bình luận (0)
Cho hai đường thẳng d1 2x - 3y +1 = 0 và d2 -4x + 6y -3 = 0
viết đường thẳng // với d1 và d2
Đường thẳng song song với d1 và d2 là:
(d3): 2x - 3y + c (với c khác 1 và c khác 1,5)
Đúng 0
Bình luận (0)
Trong không gian với hệt tọa độ Oxyz, cho hai đường thẳng
d
1
,
d
2
lần lượt có phương trình
d
1
:
x
−
2
2
y
−
2
1
z
−
3...
Đọc tiếp
Trong không gian với hệt tọa độ Oxyz, cho hai đường thẳng d 1 , d 2 lần lượt có phương trình d 1 : x − 2 2 = y − 2 1 = z − 3 3 , d 2 : x − 1 2 = y + 2 − 1 = z + 1 4 . Viết phương trình mặt phẳng cách đều hai đường thẳng d 1 và d 2 .
A. − 7 x + 2 y − 4 z + 13 2 = 0
B. − 7 x + 2 y − 4 z - 17 2 = 0
C. 7 x - 2 y − 4 z - 13 2 = 0
D. 7 x - 2 y − 4 z - 17 2 = 0
Trong không gian tọa độ Oxyz cho đường thẳng d1 và d2 lần lượt có phương trình
x
9
+
2
t
y
-
1
-
t...
Đọc tiếp
Trong không gian tọa độ Oxyz cho đường thẳng d1 và d2 lần lượt có phương trình x = 9 + 2 t y = - 1 - t z = 3 - t v à x = 1 - 2 t ' y = 4 + t ' z = 2 + t ' và Viết phương trình mặt phẳng chứa cả hai đường thẳng d1 và d2
Trong không gian tọa độ Oxyz cho đường thẳng
d
1
và
d
2
lần lượt có phương trình
x
9
+
2
t
y
-
1
-...
Đọc tiếp
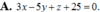
Trong không gian tọa độ Oxyz cho đường thẳng d 1 và d 2 lần lượt có phương trình x = 9 + 2 t y = - 1 - t z = 3 - t và x = 1 - 2 t ' y = 4 + t ' z = 2 + t ' Viết phương trình mặt phẳng chứa cả hai đường thẳng d 1 và d 2
