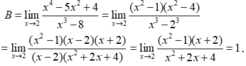GPT : x4 - 4x3 + 5x2 - 2x - 20 = 0

Những câu hỏi liên quan
Giair các phương trình
a) x4 - 4x3 - 19x2 + 106x - 120 = 0
b) 4x4 + 12x3 + 5x2 - 6x - 15 = 0
\(a,x^4-4x^3-19x^2+106x-120=0\\ \Rightarrow\left(x-4\right)\left(x^3-19x+30\right)=0\Rightarrow\left(x-4\right)\left(x+5\right)\left(x^2-5x+6\right)=0\\ \Rightarrow\left(x-4\right)\left(x+5\right)\left(x-2\right)\left(x-3\right)=0\\ \Rightarrow\left[{}\begin{matrix}x=4\\x=-5\\x=2\\x=3\end{matrix}\right.\)
Vậy pt có tập nghiệm \(S=\left\{-5;2;3;4\right\}\)
\(b,4x^4+12x^3+5x^2-6x-15=0\\ \Rightarrow\left(x-1\right)\left(4x^3+16x^2+21x+15\right)=0\\ \Rightarrow\left(x-1\right)\left[\left(4x^3+10x^2\right)+\left(6x^2+15x\right)+\left(6x+15\right)\right]=0\\ \Rightarrow\left(x-1\right)\left[2x^2\left(2x+5\right)+3x\left(2x+5\right)+3\left(2x+5\right)\right]=0\\ \Rightarrow\left(x-1\right)\left(2x+5\right)\left(2x^2+3x+3\right)=0\\ \Rightarrow\left[{}\begin{matrix}x=1\\x=-\dfrac{5}{2}\\2x^2+3x+3=0\left(vô.lí\right)\end{matrix}\right.\)
Vậy pt có tập nghiệm \(S=\left\{1;-\dfrac{5}{2}\right\}\)
Đúng 0
Bình luận (0)
Phân tích
a,(x2 + x + 2)3 - (x+1)3 x6 +1 b,(x2 + 10x + 8)2 - (8x + 4)(x2 + 8x+7)
c, A x4 + 2x3 + 3x2 + 2x+4 d,B x4 + 4x3 + +8x2 + 8x + 4
e, C x4 - 2x3 + 5x2 - 4x + 4
Đọc tiếp
Phân tích
a,(x2 + x + 2)3 - (x+1)3 = x6 +1 b,(x2 + 10x + 8)2 - (8x + 4)(x2 + 8x+7)
c, A= x4 + 2x3 + 3x2 + 2x+4 d,B= x4 + 4x3 + +8x2 + 8x + 4
e, C= x4 - 2x3 + 5x2 - 4x + 4
b: \(\left(x^2+10x+8\right)^2-\left(8x+4\right)\left(x^2+8x+7\right)\)
\(=\left\lbrack\left(x^2+8x+7\right)+\left(2x+1\right)\right\rbrack^2-4\left(2x+1\right)\left(x^2+8x+7\right)\)
\(=\left(x^2+8x+7\right)^2+2\left(x^2+8x+7\right)\left(2x+1\right)+\left(2x+1\right)^2-4\left(2x+1\right)\left(x^2+8x+7\right)\)
\(=\left(x^2+8x+7\right)^2-2\left(x^2+8x+7\right)\left(2x+1\right)+\left(2x+1\right)^2\)
\(=\left(x^2+8x+7-2x-1\right)^2=\left(x^2+6x+6\right)^2\)
d: \(B=x^4+4x^3+8x^2+8x+4\)
\(=x^4+2x^3+2x^2+2x^3+4x^2+4x+2x^2+4x+4\)
\(=x^2\left(x^2+2x+2\right)+2x\left(x^2+2x+2\right)+2\left(x^2+2x+2\right)\)
\(=\left(x^2+2x+2\right)\left(x^2+2x+2\right)=\left(x^2+2x+2\right)^2\)
e: \(C=x^4-2x^3+5x^2-4x+4\)
\(=x^4-x^3+2x^2-x^3+x^2-2x+2x^2-2x+4\)
\(=x^2\left(x^2-x+2\right)-x\left(x^2-x+2\right)+2\left(x^2-x+2\right)=\left(x^2-x+2\right)\left(x^2-x+2\right)\)
\(=\left(x^2-x+2\right)^2\)
Đúng 0
Bình luận (0)
Hãy sắp xếp các hạng tử của mỗi đa thức sau theo lũy thừa giảm dần của biến:
Q(x) = 4x3 – 2x + 5x2 - 2x3 + 1 - 2x3
R(x) = -x2 + 2x4 + 2x - 3x4 – 10 + x4
Trước hết, ta rút gọn các đa thức:
- Q(x) = 4x3 – 2x + 5x2 - 2x3 + 1 - 2x3
Q(x) = (4x3- 2x3- 2x3) – 2x + 5x2 + 1
Q(x) = 0 – 2x + 5x2 + 1
Q(x) = – 2x + 5x2 + 1
- R(x) = - x2 + 2x4 + 2x - 3x4 – 10 + x4
R(x) = - x2 + (2x4- 3x4+ x4) + 2x – 10
R(x) = - x2 + 0 + 2x – 10
R(x) = - x2 + 2x – 10
Sắp xếp các hạng tử của đa thức sau theo lũy thừa giảm dần của biến ta có:
Q(x) = 5x2 – 2x + 1
R(x) = - x2 + 2x – 10
Đúng 0
Bình luận (0)
Tìm giới hạn B = lim x → 2 x 4 - 5 x 2 + 4 x 3 - 8 .
A. 4
B. 3
C. 2
D. 1
11) a6 + a4 + a2b2 + b4 - b6
12) x3 + 3xy + y3 - 1
13) 4x4 + 4x3 + 5x2 + 2x + 1
14) x8 + x + 1
15) x8 + 3x4 + 4
16) 3x2 + 22xy + 11x + 37y + 7y2 +10
17) x4 - 8x + 63
11) Ta có: \(a^6+a^4+a^2b^2+b^4-b^6\)
\(=a^6-b^6+a^4+a^2b^2+b^4\)
\(=\left(a^2-b^2\right)\left(a^4+a^2b^2+b^4\right)+\left(a^4+a^2b^2+b^4\right)\)
\(=\left(a^4+a^2b^2+b^4\right)\left(a^2-b^2+1\right)\)
12) Ta có: \(x^3+3xy+y^3-1\)
\(=\left(x^3+3x^2y+3xy^2+y^3-1\right)-3x^2y-3xy^2+3xy\)
\(=\left[\left(x+y\right)^3-1\right]-3xy\left(x+y-1\right)\)
\(=\left(x+y-1\right)\left[x^2+2xy+y^2+x+y+1\right]-3xy\left(x+y-1\right)\)
\(=\left(x+y-1\right)\left(x^2-xy+y^2+x+y+1\right)\)
14) Ta có: \(x^8+x+1\)
\(=x^8+x^7-x^7-x^6+x^6+x^5-x^5-x^4+x^4+x^3-x^3+x^2-x^2+x+1\)
\(=x^6\left(x^2+x+1\right)-x^5\left(x^2+x+1\right)+x^3\left(x^2+x+1\right)-x^2\left(x^2+x+1\right)+\left(x^2+x+1\right)\)
\(=\left(x^2+x+1\right)\left(x^6-x^5+x^3-x^2+1\right)\)
15) Ta có: \(x^8+3x^4+4\)
\(=x^8+4x^4+4-x^4\)
\(=\left(x^4+2\right)^2-\left(x^2\right)^2\)
\(=\left(x^4-x^2+2\right)\left(x^4+x^2+2\right)\)
Đúng 2
Bình luận (0)
Cho hai đa thức
A
(
x
)
3
x
4
-
4
x
3
+
5
x
2
-
3
-
4
x
,
B
(
x
)
-
3
x
4
+
4
x
3
-
5
x...
Đọc tiếp
Cho hai đa thức A ( x ) = 3 x 4 - 4 x 3 + 5 x 2 - 3 - 4 x , B ( x ) = - 3 x 4 + 4 x 3 - 5 x 2 + 6 + 2 x . Tổng của đa thức A ( x ) + B ( x ) là:
A. - 10 x 2 - 2 x - 3
B. -2x + 3
C. 8 x 3 - 4 x + 3
D. -6x - 9
Chọn B
Ta có A(x) + B(x) = (3x4 - 4x3+ 5x2 - 3-4x) + (-3x4+ 4x3 - 5x2+ 6 + 2x) = -2x + 3.
Đúng 0
Bình luận (0)
Ta có :
\(3x^4-4x^3+5x^2-3-4x-3x^4+4x^3-5x^2+6+2x\)
\(=3-2x\)hay \(-2x+3\)
Suy ra : Ta chọn B
3x4 - 4x3 + 5x2 - 3 - 4x - 3x4 + 4x3 - 5x2 + 6 + 2x
= 3 - 2x
CHON B
giải bất phương trình x4 - 5x2 + 2x+3 < 0
\(\Leftrightarrow\left(x^4+x^3-3x^2\right)-\left(x^3+x^2-3x\right)-\left(x^2+x-3\right)< 0\)
\(\Leftrightarrow x^2\left(x^2+x-3\right)-x\left(x^2+x-3\right)-1\left(x^2+x-3\right)< 0\)
\(\Leftrightarrow\left(x^2-x-1\right)\left(x^2+x-3\right)< 0\)
\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{-1-\sqrt{13}}{2}< x< \dfrac{1-\sqrt{5}}{2}\\\dfrac{-1+\sqrt{13}}{2}< x< \dfrac{1+\sqrt{5}}{2}\end{matrix}\right.\)
Đúng 2
Bình luận (0)
1/ Cho 2 đa thức:
A (x) = 3x4 - 4x3 + 5x2 - 4x - 3
B (x) = - 3x4 + 4x3 - 5x2 + 2x + 6
a) Tính C (x) = A (x) + B (x)
b) Tìm nghiệm của đa thức C (x)
a: \(C\left(x\right)=A\left(x\right)+B\left(x\right)\)
\(=3x^4-4x^3+5x^2-4x-3-3x^4+4x^3-5x^2+2x+6\)
=-2x+3
b: Đặt C(x)=0
=>-2x+3=0
hay x=3/2
Đúng 0
Bình luận (0)
Giải hộ e bài này với ai 👍
Câu 1 : a, 4x2 -3x-1=0 / d, 4x4-5x2+1=0
b, x2 - (1+căn 5)x + căn 5= 0 / e,x2 +3=|4x| / f, 2x + 5cănx +3 =0 / g, (x2 +x +1 ).(x2+x+2)=2 / h, x4-5x2+4=0
c, x4 + x2 -20=0 / k, x phần x2-1 -- 1 phần 2(x+1) = 1phan 2
1,2-(x-0,8)=-2.(0,9+x)
2x(x+3)-x-3=0
x2-4=3(x-2)
(x+2)(3-4x)=x2+4x+4
x3-5x2+6x=0
bạn cứ tra gg rồi ấn thừa số là ra
kinh nghiệm đó
1000%
Đúng 1
Bình luận (0)