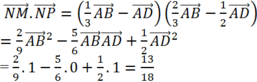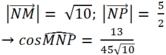Cho hình vuông ABCD cạnh 1cm. M là trung điểm BC. Trên các CD lấy điểm N sao cho góc MAN = 45 độ. Tính độ dài DN.

Những câu hỏi liên quan
Cho hình chóp S.ABCD có ABCD là hình vuông cạnh a, cạnh bên SA vuông với đáy. Trên cạnh BC lấy điểm M di động và cạnh CD lấy N di động sao cho góc MAN=45 độ. Gọi BM=x, DN=y và (0<x;y<a)
Chứng minh a(x+y)=a2-xy
Cho hình vuông ABCD. M là trung điểm BC. Trên các CD lấy điểm N sao cho góc MAN =45 độ . Chứng minh CD = 3ND .
Giúp mình đi. Mai là hạn rồi. Giải chi tiết nhá
cho hình vuông ABCD có cạnh bằng 6cm. Điểm N nằm trên cạnh CD sao choDN =2 cm, P là điểm nằm trên tia đối của BC sao cho BP=DN
a. cm tg ABP=ADN và tg ANCP nội tiếp đt
b, tính độ dài đt ngoại tiếp tứ giác ANCP
c, trên cạnh BC lấy điểm M sao cho góc MAN = 45 độ. cm MP=MN và tính diện tích tam giác AMN
giúp mình câu c, diện tích vs ạaaa ạ
1 Hình vuông ABCD có cạnh AB=a. Gọi M là trung điểm của cạnh BC. Trên cạnh CD ta lấy điểm N sao cho khoảng cách từ đó đến đường thẳng AM bằng độ dài đoạn thẳng DN. Tính độ dài các đoạn thẳng AM, CN, MN
2 Cho tam giác vuông ABC vuông tại B có AB=3a, BC=4a. Ta dựng tam giác ACD vuông cân tại D sao cho D khác phía với B đối vớ đường thẳng AC. Tính độ dài AD,BD
Cho hình vuông ABCD cạnh bằng 1. Trên cạnh AB lấy điểm M sao cho BM 1, trên cạnh CD lấy điểm N sao cho DN 1 và P là trung điểm BC. Tính cosMNP?
Đọc tiếp
Cho hình vuông ABCD cạnh bằng 1. Trên cạnh AB lấy điểm M sao cho BM = 1, trên cạnh CD lấy điểm N sao cho DN = 1 và P là trung điểm BC. Tính cosMNP?
![]()
![]()
![]()
![]()
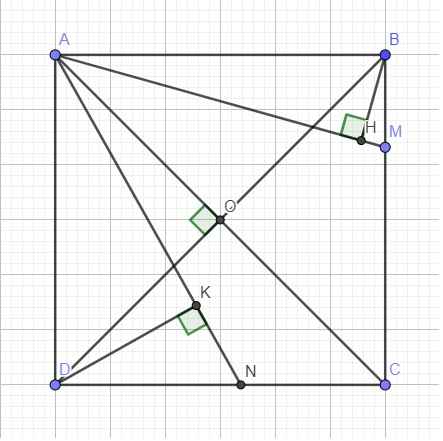
Cho hình vuông ABCD có cạnh bằng a tâm O, hai điểm di động M,N lần lượt trên hai cạnh BC, CD sao cho góc MAN= 45 độ. Gọi H, K lần lượt là hình chiếu của B, D trên AM, AN
a). Chứng minh tg ABHO, ADKO nội tiếp khi BM= DN= \(\dfrac{a}{3}\)
b) Chứng minh \(\dfrac{AH}{AN}=\dfrac{AK}{AM}\)
Chi tiết \(BM=DN=\dfrac{a}{3}\) hoàn toàn không cần thiết
a.
Ta có: \(AC\perp BD\) tại O (2 đường chéo hình vuông) \(\Rightarrow O\) thuộc đường tròn đường kính AB
\(AH\perp BH\) (gt) \(\Rightarrow\) H thuộc đường tròn đường kính AB
\(\Rightarrow\) 4 điểm A,B,O,H cùng thuộc đường tròn đường kính AB hay tứ giác ABHO nội tiếp
Hoàn toàn tương tự, 4 điểm ADKO cùng thuộc đường tròn đường kính AD nên tứ giác ADKO nội tiếp
b.
Trong tam giác vuông ABM vuông tại B với đường cao BH, áp dụng hệ thức lượng:
\(AB^2=AH.AM\)
Tương tự, trong tam giác vuông ADN:
\(AD^2=AK.AN\)
Mà \(AB=AD=a\Rightarrow AH.AM=AK.AN\Rightarrow\dfrac{AH}{AN}=\dfrac{AK}{AM}\) (đpcm)
Đúng 1
Bình luận (0)
Cho hình vuông ABCD. Gọi M,N là hai điểm lần lượt trên hai cạnh BC và CD sao cho góc MAN= 45 độ. Chứng minh chu vi tam giác CMN = 1/2 chu vi hình vuông ABCD
Trên tia đối của tia DC lấy E sao cho DE=BM
Xét ΔABM vuông tại B và ΔADE vuông tại D có
AB=AD
BM=DE
=>ΔABM=ΔADE
=>AM=AE
góc BAM+góc MAN+góc NAD=góc BAD=90 độ
=>góc BAM+góc NAD=45 độ
=>góc EAN=45 độ
Xét ΔEAN và ΔMAN có
AE=AM
góc EAN=góc MAN
AN chung
=>ΔEAN=ΔMAN
=>EN=MN
C CMN=CM+MN+CN
=CM+MN+CN
=CM+ED+DN+CN
=CM+BM+DN+CN
=BC+CD=1/2*C ABCD
Đúng 0
Bình luận (0)
Cho hình vuông ABCD có cạnh bằng a. Trên BC, CD lần lượt lấy các điểm M,N sao cho góc MAN bằng 45 ° (M khác B, N khác C, M khác C, N khác D). Từ A kẻ AK vuông góc với MN (K thuộc MN). C/m: KM=MB và DN=NK
Tự vẽ hình nhé
Tạo hình: lấy điểm T thuộc đường thẳng DC( T không nằm trên đọan DC) sao cho góc DAT = góc BAM
lấy điểm H thuộc đường thẳng BC( H không nằm trên đọan BC) sao cho góc BAH = góc DAN.
Bạn tự c/m: \(\hept{\begin{cases}\Delta ATD=\Delta AMB\\\Delta ADN=\Delta ABH\end{cases}\Rightarrow\hept{\begin{cases}AT=AM\\AN=AH\end{cases}}}\) ( 2 cạnh tương ứng )
Tiếp theo c/m \(\hept{\begin{cases}\Delta TAN=\Delta MAN\\\Delta MAN=\Delta MAH\end{cases}\Rightarrow\hept{\begin{cases}\widehat{TNA}=\widehat{MNA}\\\widehat{NMA}=\widehat{HMA}\end{cases}}}\)( 2 góc tương ứng )
Đến đây bạn tự làm nốt nhé
Đúng 0
Bình luận (0)
Hình vuông ABCD có cạnh AB=a. Gọi M là trung điểm của các cạnh BC.Trên cạnh CD lấy điểm N sao cho khoảng cách từ đó đến đường thẳng AM bằng độ dài đoạn DN. Tính AM,CN,MN
Vẽ \(NP\perp AM\) tại P
\(\hept{\begin{cases}\text{có }AB=a\Rightarrow AM=\sqrt{AB^2+BN^2}=\frac{\sqrt{5}}{2}a\\\text{từ }CM:AM=AD=a\end{cases}}\Rightarrow MP=\frac{-2+\sqrt{5}}{2}a\)
Đặt ND = NP, ta có:
\(x^2+MP^2=MC^2+CN^2\)
\(x^2+\left(\frac{-2+\sqrt{5}}{2}\right)^2a^2=\frac{a^2}{4}+\left(a-x\right)^2\)
\(\Leftrightarrow x^2+\frac{9-4\sqrt{5}}{4}a^2=\frac{a^2}{4}+a^2-2ax+x^2\)
\(\Leftrightarrow a^2\left(\frac{9-4\sqrt{5}}{4}-\frac{1}{4}-1\right)=-2ax\)
\(\Leftrightarrow\left(1-\sqrt{5}\right)a^2=-2ax\)
\(\Leftrightarrow x=\frac{\sqrt{5}-1}{2}a\Rightarrow CN=\frac{3-\sqrt{5}}{2}a\)
\(\Rightarrow MN=\sqrt{CN^2+MC^2}\)
\(MN=\sqrt{\frac{15-6\sqrt{5}}{4}a^2}\)
\(MN=\sqrt{\frac{15-6\sqrt{5}}{2}}a\)
P/s: Ko chắc
Đúng 0
Bình luận (0)