phân thức được xác định ⇔ x² - 1 ≠ 0 ⇔ x ≠ \(\left\{-1;1\right\}\)

\(\dfrac{3x+3}{x^2-1}=-2\) 

=> 3x + 3 = -2x² + 2

=> 2x² + 3x + 1 = 0

=> (2x+1)(x+1) = 0

=> x = -1/2 (thỏa mãn) hoặc x = -1 (loại)

Vậy, để phân thức có giá trị bằng  –2 thì x = -1/2.

\(\dfrac{3x+3}{x^2-1}\)=\(\dfrac{3\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}\)  (x khác -1 và x khác 1)

= \(\dfrac{3}{x-1}\)

=> Phân thức ban đầu có giá trị nguyên ⇔ 3 chia hết cho x-1

=> x-1 ∈\(\left\{-3;-1;1;3\right\}\)

=> x ∈\(\left\{-2;0;2;4\right\}\)

Vậy, để phân thức có giá trị là số nguyên.thì x ∈\(\left\{-2;0;2;4\right\}\).

a) ĐKXĐ: \(x\notin\left\{1;-1\right\}\)

b) Ta có: \(\dfrac{3x+3}{x^2-1}\)

\(=\dfrac{3\left(x+1\right)}{\left(x+1\right)\left(x-1\right)}\)

\(=\dfrac{3}{x-1}\)

Để phân thức có giá trị bằng -2 thì \(\dfrac{3}{x-1}=-2\)

\(\Leftrightarrow x-1=-\dfrac{3}{2}\)

hay \(x=-\dfrac{1}{2}\)(thỏa ĐK)

a) ĐKXĐ: \(x\notin\left\{1;-1\right\}\)

b) Ta có: \(\dfrac{3x+3}{x^2-1}\)

\(=\dfrac{3\left(x+1\right)}{\left(x+1\right)\left(x-1\right)}\)

\(=\dfrac{3}{x-1}\)

Để phân thức có giá trị bằng -2 thì \(\dfrac{3}{x-1}=-2\)

\(\Leftrightarrow x-1=\dfrac{-3}{2}\)

hay \(x=-\dfrac{1}{2}\)

Vậy: Để phân thức có giá trị bằng -2 thì \(x=-\dfrac{1}{2}\)

c) Để phân thức có giá trị là số nguyên thì \(3⋮x-1\)

\(\Leftrightarrow x-1\inƯ\left(3\right)\)

\(\Leftrightarrow x-1\in\left\{1;-1;3;-3\right\}\)

\(\Leftrightarrow x\in\left\{2;0;4;-2\right\}\)

Kết hợp ĐKXĐ, ta được: 

\(x\in\left\{2;0;4;-2\right\}\)

Vậy: Để phân thức có giá trị là số nguyên thì \(x\in\left\{2;0;4;-2\right\}\)

Bài 1 

Ta có : \(\frac{2x+2}{x^2-1}=0\)ĐK : \(x\ne\pm1\)

\(\Leftrightarrow2x+2=0\Leftrightarrow x=-1\)( ktm )

Bài 2 : 

Ta có : \(\frac{2x+3}{-x+5}=\frac{3}{4}\)ĐK : \(x\ne5\)

\(\Leftrightarrow8x+12=-3x+15\Leftrightarrow11x=3\Leftrightarrow x=\frac{3}{11}\)

Vậy phương trình có tập nghiệm là S = { 3/11 }

a) ĐKXĐ: \(x\notin\left\{1;-1\right\}\)

b) Ta có: \(\dfrac{4x-4}{2x^2-2}\)

\(=\dfrac{4\left(x-1\right)}{2\left(x-1\right)\left(x+1\right)}\)

\(=\dfrac{2}{x+1}\)

Để phân thức có giá trị bằng -2 thì \(\dfrac{2}{x+1}=-2\)

\(\Leftrightarrow x+1=-1\)

hay x=-2(thỏa ĐK)

\(a,ĐK:x^2-1=\left(x-1\right)\left(x+1\right)\ne0\Leftrightarrow x\ne\pm1\\ \dfrac{3x+3}{x^2-1}=\dfrac{3\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{3}{x-1}=2\\ \Leftrightarrow x-1=\dfrac{3}{2}\Leftrightarrow x=\dfrac{5}{2}\left(tm\right)\\ b,\dfrac{3}{x-1}\in Z\\ \Leftrightarrow x-1\inƯ\left(3\right)=\left\{-3;-1;1;3\right\}\\ \Leftrightarrow x\in\left\{-2;0;2;4\right\}\left(tm\right)\)

Phân thức 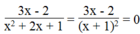 khi 3x – 2 = 0 và x + 1 2 ≠ 0

Ta có:  x + 1 2 ≠ 0  ⇔ x + 1 ≠ 0 ⇔ x ≠ - 1

3x – 2 = 0 ⇔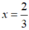 

Ta có: 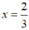 thỏa mãn điều kiện x ≠ - 1

Vậy 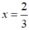 thì phân thức 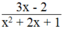có giá trị bằng 0.

a: ĐKXĐ: \(x\notin\left\{2;-2\right\}\)

b: \(C=\dfrac{x^3-x^2-2x-2x+4}{\left(x-2\right)\left(x+2\right)}=\dfrac{x^3-x^2-4x+4}{\left(x-2\right)\left(x+2\right)}\)

\(=\dfrac{x^2\left(x-1\right)-4\left(x-1\right)}{\left(x-2\right)\left(x+2\right)}=x-1\)

Để C=0 thì x-1=0

hay x=1

c: Để C>0 thì x-1>0

hay x>1

Vậy: \(\left\{{}\begin{matrix}x\in Z\backslash\left\{1\right\}\\x\notin\left\{2;-2\right\}\end{matrix}\right.\)

\(a,ĐK:x\ne1;x\ne-1\\ b,C=\dfrac{x^2+x+x^2+1}{2\left(x-1\right)\left(x+1\right)}=\dfrac{2x^2+2x+1}{2x^2-2}\\ c,C=-\dfrac{1}{2}\Leftrightarrow2-2x^2=2x^2+2x+1\\ \Leftrightarrow4x^2+2x-1=0\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\sqrt{5}-1}{4}\\x=\dfrac{-\sqrt{5}-1}{4}\end{matrix}\right.\\ d,C>0\Leftrightarrow2x^2-2>0\left(2x^2+2x+1>0\right)\\ \Leftrightarrow\left(x-1\right)\left(x+1\right)>0\\ \Leftrightarrow\left[{}\begin{matrix}x>1\\x< -1\end{matrix}\right.\)

Phân thức 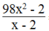 = 0 khi 98 x 2 + 2 = 0 và x – 2  ≠  0

Ta có: x – 2  ≠  0 ⇔ x  ≠  2

98 x 2 + 2 = 0  ⇔ 2 49 x 2 - 1 = 0 ⇔ (7x + 1)(7x – 1) = 0

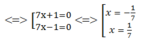
Ta có: 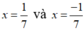 thỏa mãn điều kiện x  ≠  2

Vậy  thì phân thức  có giá trị bằng 0.

a) Điều kiện xác định của \(P\) là: 

\(\left(x+1\right)\left(2x-6\right)\ne0\Leftrightarrow\left\{{}\begin{matrix}x+1\ne0\\2x-6\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ne-1\\x\ne3\end{matrix}\right.\)

b) \(P=\dfrac{3x^2+3x}{\left(x+1\right)\left(2x-6\right)}\) (\(x\ne-1,x\ne3\))

\(=\dfrac{3x\left(x+1\right)}{2\left(x+1\right)\left(x-3\right)}=\dfrac{3x}{2\left(x-3\right)}\)

\(P=1\Rightarrow\dfrac{3x}{2\left(x-3\right)}=1\Rightarrow3x=2\left(x-3\right)\Leftrightarrow x=-6\) (thỏa mãn) 

c) \(P>0\Rightarrow\dfrac{3x}{2\left(x-3\right)}>0\Leftrightarrow\dfrac{x}{x-3}>0\)

\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x>0\\x-3>0\end{matrix}\right.\\\left[{}\begin{matrix}x< 0\\x-3< 0\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x>3\\x< 0\end{matrix}\right.\)

Kết hợp với điều kiện xác định ta được để \(P>0\) thì \(x>3\) hoặc \(x< 0,x\ne-1\).