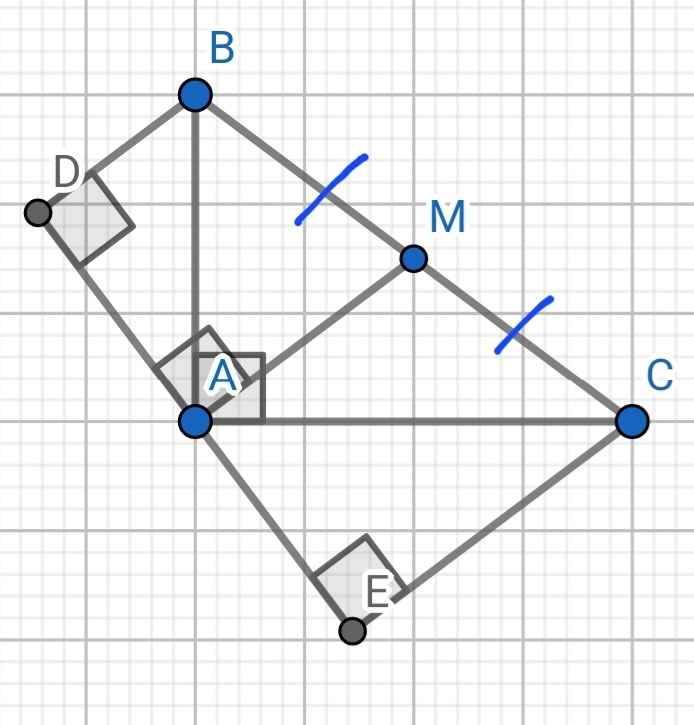
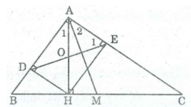
Cho ∆ ABC vuông tại A có đường trung tuyến AM . Gọi D; Klần lượt là trung điểm AB ; AC
a) chứng minh tứ giác AKMD là hình bình hành
b) gọi Elà điểm đối xứng với N qua O , CM : tứ giác EAMB là hình thoi
c) Gọi I là trung điểm AM
Cm: 3 điểm E ; I ; C thẳng hàng