Question

Cho tam giác ABC vuông tại A, đường cao AH, đường trung tuyến AM. Gọi D, E theo thứ tự là chân đường vuông góc kể từ H đến AB, AC. Chứng minh rằng AM vuông góc với DE.

Answer 1

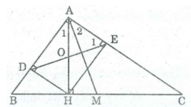
Xét tứ giác ADHE, ta có:

∠ A = 90 0  (gt)

∠ (ADH) =  90 0  (vì HD ⊥ AB)

∠ (AEH) =  90 0  (vì HE ⊥ AC)

Suy ra tứ giác ADHE là hình chữ nhật (vì có 3 góc vuông).

+ Xét ∆ ADH và  ∆ EHD có :

DH chung

AD = EH ( vì ADHE là hình chữ nhật)

∠ (ADN) =  ∠ (EHD) =  90 0

Suy ra:  ∆ ADH =  ∆ EHD (c.g.c)

⇒  ∠ A 1 =  ∠ (HED)

Lại có:  ∠ (HED) +  ∠ E 1 =  ∠ (HEA) =  90 0

Suy ra:  ∠ E 1 +  ∠ A 1 =  90 0

∠ A 1 = ∠ A 2 (chứng minh trên) ⇒  ∠ E 1 +  ∠ A 2 =  90 0

Gọi I là giao điểm của AM và DE.

Trong  ∆ AIE ta có:  ∠ (AIE) = 180o – ( ∠ E 1 +  ∠ A 2 ) = 180 0  -  90 0  =  90 0

 

Vậy AM ⊥ DE.