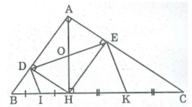
Xét tứ giác ADHE, ta có:
∠ A = 90 0 (gt)
∠ (ADH) = 90 0 (vì HD ⊥ AB)
∠ (AEH) = 90 0 (Vì HE ⊥ AC)
Suy ra tứ giác ADHE là hình chữ nhật (vì có 3 góc vuông)
Vậy AH = DE (tính chất hình chữ nhật)

Xét tứ giác ADHE, ta có:
∠ A = 90 0 (gt)
∠ (ADH) = 90 0 (vì HD ⊥ AB)
∠ (AEH) = 90 0 (Vì HE ⊥ AC)
Suy ra tứ giác ADHE là hình chữ nhật (vì có 3 góc vuông)
Vậy AH = DE (tính chất hình chữ nhật)
Cho tam giác ABC vuông tại A, đường cao AH, đường trung tuyến AM. Gọi D, E theo thứ tự là chân đường vuông góc kể từ H đến AB, AC. Chứng minh rằng AM vuông góc với DE.
Cho tam giác ABC vuông tại A, đường cao AH, đường trung tuyến AM.
a) Chứng minh rằng ∠(HAB) = ∠(MAC)
b) Gọi D, E theo thứ tự là chân đường vuông góc kể từ H đến AB, AC. Chứng
minh rằng AM vuông góc với DE.
Cho tam giác ABC vuông tại A, đường cao AH. Gọi D, E theo thứ tự là chân
đường vuông góc kể từ H đến AB, AC.
a) Chứng minh rằng AH = DE
b) Gọi I là trung điểm của HB, K là trung điểm của HC. Chứng minh rằng DI //
EK
Cho tam giác ABC vuông tại A, đường cao AH. Gọi D, E theo thứ tự là chân đường vuông góc kể từ H đến AB, AC. Gọi I là trung điểm của HB, K là trung điểm của HC. Chứng minh rằng DI // EK
Cho tam giác ABC vuông tại A, đường cao AH. Gọi D, E theo thứ tự là chân đường vuông góc kẻ từ H đến AB, AC
a, Chứng minh AH=DE
b, Gọi I, K theo thứ tự là trung điểm của HB và HC. Chứng minh tứ giác IDKE là hình thang vuông
Cho tam giác ABC vuông tại A, đường cao AH. Gọi D, E theo thứ tự là chân đường
vuông góc kẻ từ H đến AB, AC. Gọi M là trung điểm của BC. Chứng minh AM vuông góc với DE.
Cho tam giác ABC vuông tại A, đường cao AH. Gọi D, E theo thứ tự là chân đường
vuông góc kẻ từ H đến AB, AC.
1) Chứng minh: AH = DE
2) Từ D và E lần lượt kẻ các đường thẳng vuông góc với DE, hai đường thẳng này cắt cạnh BC
lần lượt tại M và N. Chứng minh M và N lần lượt là trung điểm của BH và HC.
Cho tam giác ABC vuông tại A, đường cao AH. Gọi D, E theo thứ tự là chân đường vuông góc kể từ H đến AB, AC.
a. Chứng minh rằng AH = DE
b. Gọi I là trung điểm của HB, K là trung điểm của HC. Chứng minh rằng DI // EK
Cho tam giác ABC vuông tại A, đường cao AH. Gọi D, E theo thứ tự là chân các đường vuông góc kẻ từ H đến AB, AC
a) chứng minh tứ giác ADHE là hình chữ nhật
b) gọi K là trung điểm của HC. Chứng minh rằng DE ⊥ EK