giải phương trình
1/sin+(x-3π/2) = 4sin(7π/4-x)
Tổng các nghiệm thuộc đoạn [0; 3π] của phương trình 1 - 2 cos^2 x - sin x = 0 là
A. 5/3π. B. 4π. C. 6π. D. 7/2π .
\(1-2cos^2x-sinx=0\)
\(\Leftrightarrow1-2\left(1-sin^2x\right)-sinx=0\)
\(\Leftrightarrow2sin^2x-sinx-1=0\Rightarrow\left[{}\begin{matrix}sinx=1\\sinx=-\dfrac{1}{2}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k2\pi\\x=-\dfrac{\pi}{6}+k2\pi\\x=\dfrac{7\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Rightarrow x=\left\{\dfrac{\pi}{2};\dfrac{7\pi}{6};\dfrac{11\pi}{6};\dfrac{5\pi}{2}\right\}\)
\(\Rightarrow\sum x=6\pi\)
Giải các phương trình lượng giác sau:
1) a/ \(cos\left(10x+12\right)+4\sqrt{2}sin\left(5x+6\right)-4=0\)
b/ \(cos\left(4x+2\right)+3sin\left(2x+1\right)=2\)
2) a/ \(cos2x+sin^2x+2cosx+1=0\)
b/ \(4sin^22x-8cos^2x+ 3=0\)
c/ \(4cos2x+4sin^2x+4sinx=1\)
3) a/ \(tanx+cotx=2\)
b/ \(2tanx-2cotx=3\)
4) a/ \(2sin2x+8tanx=9\sqrt{3}\)
b/ \(2cos2x+tan^2x=5\)
5) a/ \(\left(3+cotx\right)^2=5\left(3+cotx\right)\)
b/ \(4\left(sin^2x+\dfrac{1}{sin^2x}\right)-4\left(sinx+\dfrac{1}{sinx}\right)=7\)
1a.
Đặt \(5x+6=u\)
\(cos2u+4\sqrt{2}sinu-4=0\)
\(\Leftrightarrow1-2sin^2u+4\sqrt{2}sinu-4=0\)
\(\Leftrightarrow2sin^2u-4\sqrt{2}sinu+3=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinu=\dfrac{3\sqrt{2}}{2}>1\left(loại\right)\\sinu=\dfrac{\sqrt{2}}{2}\end{matrix}\right.\)
\(\Rightarrow sin\left(5x+6\right)=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}5x+6=\dfrac{\pi}{4}+k2\pi\\5x+6=\dfrac{3\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{6}{5}+\dfrac{\pi}{20}+\dfrac{k2\pi}{5}\\x=-\dfrac{6}{5}+\dfrac{3\pi}{20}+\dfrac{k2\pi}{5}\end{matrix}\right.\)
1b.
Đặt \(2x+1=u\)
\(cos2u+3sinu=2\)
\(\Leftrightarrow1-2sin^2u+3sinu=2\)
\(\Leftrightarrow2sin^2u-3sinu+1=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinu=1\\sinu=\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}sin\left(2x+1\right)=1\\sin\left(2x+1\right)=\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+1=\dfrac{\pi}{2}+k2\pi\\2x+1=\dfrac{\pi}{6}+k2\pi\\2x+1=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{2}+\dfrac{\pi}{4}+k\pi\\x=-\dfrac{1}{2}+\dfrac{\pi}{12}+k\pi\\x=-\dfrac{1}{2}+\dfrac{5\pi}{12}+k\pi\end{matrix}\right.\)
2a.
\(cos^2x-sin^2x+sin^2x+2cosx+1=0\)
\(\Leftrightarrow cos^2x+2cosx+1=0\)
\(\Leftrightarrow\left(cosx+1\right)^2=0\)
\(\Leftrightarrow cosx=-1\)
\(\Leftrightarrow x=\pi+k2\pi\)
Tính tổng tất cả các nghiệm của phương trình sin 2 x + 4 sin x - 2 cos x - 4 = 0 trong đoạn [ 0 ; 100 π ] của phương trình:
A . 2476 π
B . 25 π
C . 2475 π
D . 100 π
Tính tổng các nghiệm của phương trình
sin 2x + 4sin x - 2cos x - 4 = 0 trên đoạn 0 ; 100 π
A. 2476 π
B. 25 π
C. 2475 π
D. 100 π
Đáp án C
2sin x cos x + 4 sin x - 2 cos x - 4 = 0
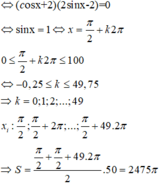
Giải các phương trình sau:
1) tan x + tan 2x + tan 3x = 0
2) cos 2x. cos 4x = \(\frac{\text{1}}{\text{2}}\)
3) cot x - tan x = cos x - sin x
4) 4sin x. sin 2x. sin 4x = sin 3x
a. ĐKXĐ: ...
\(\frac{sinx}{cosx}+\frac{sin2x}{cos2x}+\frac{sin3x}{cos3x}=0\)
\(\Leftrightarrow\frac{sin2x.cosx+cos2x.sinx}{cosx.cos2x}+\frac{sin3x}{cos3x}=0\)
\(\Leftrightarrow\frac{sin3x}{cosx.cos2x}+\frac{sin3x}{cos3x}=0\)
\(\Leftrightarrow sin3x\left(\frac{cosx.cos2x+cos3x}{cosx.cos2x.cos3x}\right)=0\)
\(\Leftrightarrow sin3x\left(\frac{cosx\left(2cos^2x-1\right)+4cos^3x-3cosx}{cosx.cos2x.cos3x}\right)=0\)
\(\Leftrightarrow sin3x\left(\frac{6cos^2x-4}{cos2x.cos3x}\right)=0\)
\(\Leftrightarrow sin3x\left(\frac{3cos2x-1}{cos2x.cos3x}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sin3x=0\\cos2x=\frac{1}{3}\end{matrix}\right.\)
b.
\(cos2x\left(2cos^22x-1\right)=\frac{1}{2}\)
\(\Leftrightarrow4cos^32x-2cos2x-1=0\)
Pt bậc 3 này ko giải được, chắc bạn ghi nhầm đề
c. ĐKXĐ: ...
\(\frac{cosx}{sinx}-\frac{sinx}{cosx}=cosx-sinx\)
\(\Leftrightarrow\frac{\left(cosx-sinx\right)\left(cosx+sinx\right)}{sinx.cosx}=cosx-sinx\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx-sinx=0\Rightarrow x=...\\\frac{cosx+sinx}{sinx.cosx}=1\left(1\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow cosx+sinx=sinx.cosx\)
Đặt \(sinx+cosx=t\Rightarrow\left\{{}\begin{matrix}\left|t\right|\le\sqrt{2}\\sinx.cosx=\frac{t^2-1}{2}\end{matrix}\right.\)
\(\Rightarrow t=\frac{t^2-1}{2}\Rightarrow t^2-2t-1=0\Rightarrow\left[{}\begin{matrix}t=1+\sqrt{2}\left(l\right)\\t=1-\sqrt{2}\end{matrix}\right.\)
\(\Rightarrow\sqrt{2}sin\left(x+\frac{\pi}{4}\right)=1-\sqrt{2}\Rightarrow sin\left(x+\frac{\pi}{4}\right)=\frac{1-\sqrt{2}}{\sqrt{2}}\Rightarrow x=...\)
d.
\(\Leftrightarrow2\left(cosx-cos3x\right)sin4x=sin3x\)
\(\Leftrightarrow2sin4x.cosx-2sin4x.cos3x=sin3x\)
\(\Leftrightarrow sin5x+sin3x-sin7x-sinx=sin3x\)
\(\Leftrightarrow sin5x-sin7x-sinx=0\)
\(\Leftrightarrow-2cos6x.sinx-sinx=0\)
\(\Leftrightarrow sinx\left(2cos6x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=0\\cos6x=-\frac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow...\)
Tìm số nghiệm thuộc khoảng ( π 2 ; 3π) của phương trình:
sin(2x + 5 π 7 ) - 3cos(x - 7 π 2 ) = 1 + 2sinx (*)
A: 3
B: 4
C: 5
D: 6
\(4sin^2\dfrac{x}{2}-\sqrt{3}cos2x=1+cos^2\left(x-\dfrac{3\pi}{4}\right)\).Giải phương trình
a) \(sinx=-\dfrac{6}{5}\)
b) \(sin3x=\dfrac{\sqrt{3}}{2}\)
c) \(sin\left(x+\dfrac{\pi}{3}\right)=sin\dfrac{3\pi}{4}\)
d) \(4sin\left(x+\dfrac{5\pi}{6}\right)=5\)
a: sin x=-6/5=-1,2
mà -1<=sin x<=1
nên \(x\in\varnothing\)
b: sin3x=căn 3/2
=>3x=pi/3+k2pi hoặc 3x=2/3pi+k2pi
=>x=pi/9+k2pi/3 hoặc x=2/9pi+k2pi/3
c: \(sin\left(x+\dfrac{pi}{3}\right)=sin\left(\dfrac{3}{4}pi\right)\)
=>x+pi/3=3/4pi+k2pi hoặc x+pi/3=1/4pi+k2pi
=>x=5/12pi+k2pi hoặc x=-1/12pi+k2pi
d: =>sin(x+5/6pi)=5/4
mà sin(x+5/6pi) thuộc [-1;1]
nên \(x\in\varnothing\)
Giải phương trình lượng giác sau: ( dạng pt bậc nhất theo sin và cos )
3cosx + 4sinx + 6/3cosx+ 4sinx+1 =2
Đề như vậy hả bạn: \(\frac{3cosx+4sinx+6}{3cosx+4sinx+1}=2\)