Tìm giá trị nhỏ nhất của biểu thức
P= \(x^2+y^2-4x+2y+5\)
a, Tìm giá trị lớn nhất của biểu thức: A=4x-x^2+3
b. Tìm giá trị nhỏ nhất của biểu thức:B=4x^2-12x+15
c,Tìm giá trị nhỏ nhất của biểu thức:C=4x^2+2y^2-4xy-4y+1
a)
\(A=4x-x^2+3=-\left(x^2-4x-3\right)=-\left(x^2-4x+4\right)+7=-\left(x-2\right)^2+7\le7\)
Daaus = xayr ra khi: x = 2
b) \(B=4x^2-12x+15=4\left(x^2-3x+9\right)-21=4\left(x-3\right)^2-21\ge-21\)
Dấu = xảy ra khi x = 3
c) \(C=4x^2+2y^2-4xy-4y+1=\left(4x^2-4xy+y^2\right)+\left(y^2-4y+4\right)-3=\left(2x-y\right)^2+\left(y-2\right)^2-3\ge-3\)
Dấu = xảy ra khi
2x = y và y = 2
=> x = 1 và y = 2
a) A = \(-x^2+4x+3=-\left(x-2\right)^2+7\le7\)
Dấu "=" <=> x = 2
b) \(4x^2-12x+15=\left(2x-3\right)^2+6\ge6\)
Dấu "=" xảy ra <=> \(x=\dfrac{3}{2}\)
c) \(4x^2+2y^2-4xy-4y+1\)
= \(\left(4x^2-4xy+y^2\right)+\left(y^2-4y+4\right)-3\)
= \(\left(2x-y\right)^2+\left(y-2\right)^2-3\ge-3\)
Dấu "=" <=> \(\left\{{}\begin{matrix}x=1\\y=2\end{matrix}\right.\)
a) Tìm giá trị nhỏ nhất của biểu thức: A = 4x2 - 12x + 100
b) Tìm giá trị lớn nhất của biểu thức: B = -x2 - x + 1
c) Tìm giá trị nhỏ nhất của biểu thức: C = 2x2 + 2xy + y2 - 2x + 2y + 2
a) \(A=4x^2-12x+100=\left(2x\right)^2-12x+3^2+91=\left(2x-3\right)^2+91\)
Ta có: \(\left(2x-3\right)^2\ge0\forall x\inℤ\)
\(\Rightarrow\left(2x-3\right)^2+91\ge91\)
hay A \(\ge91\)
Dấu "=" xảy ra <=> \(\left(2x-3\right)^2=0\)
<=> 2x-3=0
<=> 2x=3
<=> \(x=\frac{3}{2}\)
Vậy Min A=91 đạt được khi \(x=\frac{3}{2}\)
b) \(B=-x^2-x+1=-\left(x^2+x-1\right)=-\left(x^2+x+\frac{1}{4}-\frac{5}{4}\right)=-\left(x+\frac{1}{2}\right)^2+\frac{5}{4}\)
Ta có: \(-\left(x+\frac{1}{2}\right)^2\le0\forall x\)
\(\Rightarrow-\left(x+\frac{1}{2}\right)^2+\frac{5}{4}\le\frac{5}{4}\) hay B\(\le\frac{5}{4}\)
Dấu "=" \(\Leftrightarrow-\left(x+\frac{1}{2}\right)^2=0\)
\(\Leftrightarrow x+\frac{1}{2}=0\)
\(\Leftrightarrow x=\frac{-1}{2}\)
Vậy Max B=\(\frac{5}{4}\)đạt được khi \(x=\frac{-1}{2}\)
\(C=2x^2+2xy+y^2-2x+2y+2\)
\(C=x^2+2x\left(y-1\right)+\left(y-1\right)^2+x^2+1\)
\(\Leftrightarrow C=\left(x+y-1\right)^2+x^2+1\)
Ta có:
\(\hept{\begin{cases}\left(x+y-1\right)^2\ge0\forall x;y\inℤ\\x^2\ge0\forall x\inℤ\end{cases}}\)
\(\Leftrightarrow\left(x+y-1\right)^2+x^2+1\ge1\)
hay C\(\ge\)1
Dấu "=" xảy ra khi \(\hept{\begin{cases}\left(x+y-1\right)^2=0\\x^2=0\end{cases}\Leftrightarrow\hept{\begin{cases}x+y=1\\x=0\end{cases}\Leftrightarrow}\hept{\begin{cases}y=1\\x=0\end{cases}}}\)
Vậy Min C=1 đạt được khi y=1 và x=0
Tìm giá trị nhỏ nhất của biểu thức: E= 4x^2+y^2-4x-2y+3; F=3/2x^2+x+1; G = x^2+2y^2+2xy-2y . Giúp mk nhé. Gấp lắm
Câu 1 :
\(E=4x^2+y^2-4x-2y+3\)
\(E=\left(2x\right)^2-2\cdot2x\cdot1+1^2+y^2-2\cdot y\cdot1+1^2+1\)
\(E=\left(2x-1\right)^2+\left(y-1\right)^2+1\ge1\forall x;y\)
Dấu "=" xảy ra \(\Leftrightarrow\hept{\begin{cases}2x-1=0\\y-1=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=\frac{1}{2}\\y=1\end{cases}}\)
Câu 2 :
\(G=x^2+2y^2+2xy-2y\)
\(G=x^2+2xy+y^2+y^2-2.y\cdot1+1^2-1\)
\(G=\left(x+y\right)^2+\left(y-1\right)^2-1\ge-1\forall x;y\)
Dấu "=" xảy ra \(\Leftrightarrow\hept{\begin{cases}x+y=0\\y-1=0\end{cases}\Leftrightarrow\hept{\begin{cases}x+1=0\\y=1\end{cases}\Leftrightarrow}\hept{\begin{cases}x=-1\\y=1\end{cases}}}\)
\(F=\frac{3}{2x^2+x+1}=\frac{3}{2\left(x^2+\frac{x}{2}+\frac{1}{2}\right)}=\frac{3}{2\left(x^2+2x\cdot\frac{1}{4}+\frac{1}{16}\right)+\frac{7}{8}}=\frac{3}{2\left(x+\frac{1}{4}\right)^2+\frac{7}{8}}\)
Vi \(2\left(x+\frac{1}{4}\right)^2\ge0\Rightarrow2\left(x+\frac{1}{4}\right)^2+\frac{7}{8}\ge8\)
\(\Rightarrow\frac{1}{2\left(x+\frac{1}{4}\right)^2+\frac{7}{8}}\le\frac{1}{\frac{7}{8}}\Rightarrow F=\frac{3}{2\left(x+\frac{1}{4}\right)^2+\frac{7}{8}}\le\frac{3}{\frac{7}{8}}=\frac{24}{7}\)
Dấu "=" xảy ra <=>x+1/4=0<=>x=-1/4
cho 2 số x,y thỏa mãn điều kiện:(x^2-y^2+1)^2+4x^2y^2-x^2-y^2=0.Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức x^2+y^2
Tìm giá trị nhỏ nhất của biểu thức:
a)A=x^2 + 4x - 2
b)B=2x^2 - 4x + 3
c)C=x^2 + y^2 - 4x + 2y + 5
a) A = x2 + 4x - 2 = x2 + 4x + 4 - 6 = (x + 2)2 - 6
(x + 2)2 ≥ 0 => A ≥ -6 => GTNN của A là -6, xảy ra khi x = 2
`a)A=x^2+4x-2`
`A=x^2+4x+4-6=(x+2)^2-6`
Vì `(x+2)^2 >= 0 AA x`
`<=>(x+2)^2-6 >= -6 AA x`
Hay `A >= -6 AA x`
Dấu "`=`" xảy ra`<=>(x+2)^2=0<=>x=-2`
Vậy `GTN N` của `A` là `-6` khi `x=-2`
________________________________________________
`b)B=2x^2-4x+3`
`B=2(x^2-2x+3/2)`
`B=2(x^2-2x+1)+1=2(x-1)^2+1`
Vì `2(x-1)^2 >= 0 AA x`
`<=>2(x-1)^2+1 >= 1 AA x`
Hay `B >= 1 AA x`
Dấu "`=`" xảy ra `<=>(x-1)^2=0<=>x=1`
Vậy `GTN N` của `B` là `1` khi `x=1`
__________________________________________________
`c)C=x^2+y^2-4x+2y+5`
`C=x^2-4x+4+y^2+2y+1`
`C=(x-2)^2+(y+1)^2`
Vì `(x-2)^2 >= 0 AA x` và `(y+1)^2 >= 0 AA y`
`=>(x-2)^2+(y+1)^2 >= 0 AA x,y`
Hay `C >= 0 AA x,y`
Dấu "`=`" xảy ra`<=>{((x-2)^2=0),((y+1)^2=0):}`
`<=>{(x=2),(y=-1):}`
Vậy `GTN N` của `C` là `0` khi `x=2`,y=-1
Cho x,y thỏa mãn: x2+2xy+4x+4y+2y2+3=0
Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức Q=x+y+2018
Có x^2 + 2xy + 4x + 4y + 2y^2 + 3 = 0
--> (x+y)^2 + 4(x+y) + 4+ y^2 - 1 = 0
--> (x+y+2)^2 + y^2 = 1
-->(x+y+2)^2 <= 1 ( vì y^2 >=1)
--> -1 <= x+y+2 <=1
--> 2015 <= x+y+2018 <= 2017
hay 2015 <= Q , dau bang xay ra khi x+y+2=-1 --> x+y=-3
Q<=2017, dau bang xay ra khi x+y+2=1 --> x+y=-1
Vậy giá trị nhỏ nhất của Q là 2015 khi x+y =-3
giá trị lớn nhất của Q là 2017 khi x+y=-1
giá trị lớn nhất là 2017
Tìm giá trị nhỏ nhất của biểu thức : 4x2+y2-4x-2y+3
Đặt A = 4x2 + y2 - 4x - 2y + 3
= (4x2 - 4x + 1) + (y2 - 2y + 1) + 1
= (2x - 1)2 + (y - 1)2 + 1 \(\ge1\)
Dấu "=" xảy ra <=> \(\hept{\begin{cases}2x-1=0\\y-1=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=0,5\\y=1\end{cases}}\)
Vậy Min A = 1 <=> x = 0,5 ; y = 1
Tìm giá trị nhỏ nhất của biểu thức
A= x2 + y2 - 4x - 2y + 12
\(A=x^2+y^2-4x-2y+12\)
\(=\left(x^2-4x+4\right)+\left(y^2-2x+1\right)+7\)
\(=\left(x-2\right)^2+\left(y-1\right)^2+7\ge7\)
Vậy \(A_{min}=7\Leftrightarrow\hept{\begin{cases}x-2=0\\y-1=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=2\\y=1\end{cases}}\)
tìm GTNN,GTLN của biểu thức sau
a)giá trị nhỏ nhất
A= 9x^2-x+5
b) Giá trị nhỏ nhất
B= 4x^2+2y^2+4xy+2018
c) gia tri lớn nhất
C= 3x-4x^2+10
d) giá trị lớn nhất
D= -5x^2-y^2+2xy-4x+2016
giúp mik với.GẤP LẮM Ạ
a) = 9(x2 - 2.x/2.9 + 1/324) - 9/324 +5
GTNN A = 4,97
b) = (2x +y)2 + y2 + 2018
GTNN B = 2018 khi x=0;y=0
c) = -4(x2 - 2.3x/ 4.2 + 9/16) +9/16 +10
GTLN C = 169/16
d) = -(x-y)2 - (2x +1) +1 + 2016
GTLN D = 2017
(trg bn cho bài khó dữ z, làm hại cả não tui)
Cho hai số thực x, y thỏa mãn 0 ≤ x ≤ 1 2 , 0 < y ≤ 1 và log 11 − 2 x − y = 2 y + 4 x − 1. Xét biểu thức P = 16 x 2 y − 2 x 3 y + 2 − y + 5. Gọi m, M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của P. Khi đó giá trị của biểu thức T = 4m + M bằng bao nhiêu?
A. 16
B. 18
C. 17
D. 19
Đáp án C
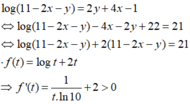
Suy ra f(t) đồng biến trên TXĐ và pt f(t) = 21 chỉ có 1 nghiệm duy nhất
Ta thấy t = 10 là 1 nghiệm của pt nên t = 10 là nghiệm duy nhất của pt
⇒ 11 − 2 x − y = 10 ⇒ y = 1 − 2 x ⇒ P = 16 x 2 ( 1 − 2 x ) − 2 x ( 3 − 6 x + 2 ) − 1 + 2 x + 5 = − 32 x 3 + 28 x 2 − 8 x + 4 P ' = − 96 x 2 + 56 x − 8 P ' = 0 ⇔ x = 1 4 x = 1 3 P ( 0 ) = 4 , P ( 1 3 ) = 88 27 , P ( 1 4 ) = 13 4 , P ( 1 2 ) = 3 ⇒ m = 13 4 , M = 4 ⇒ M + 4 m = 17