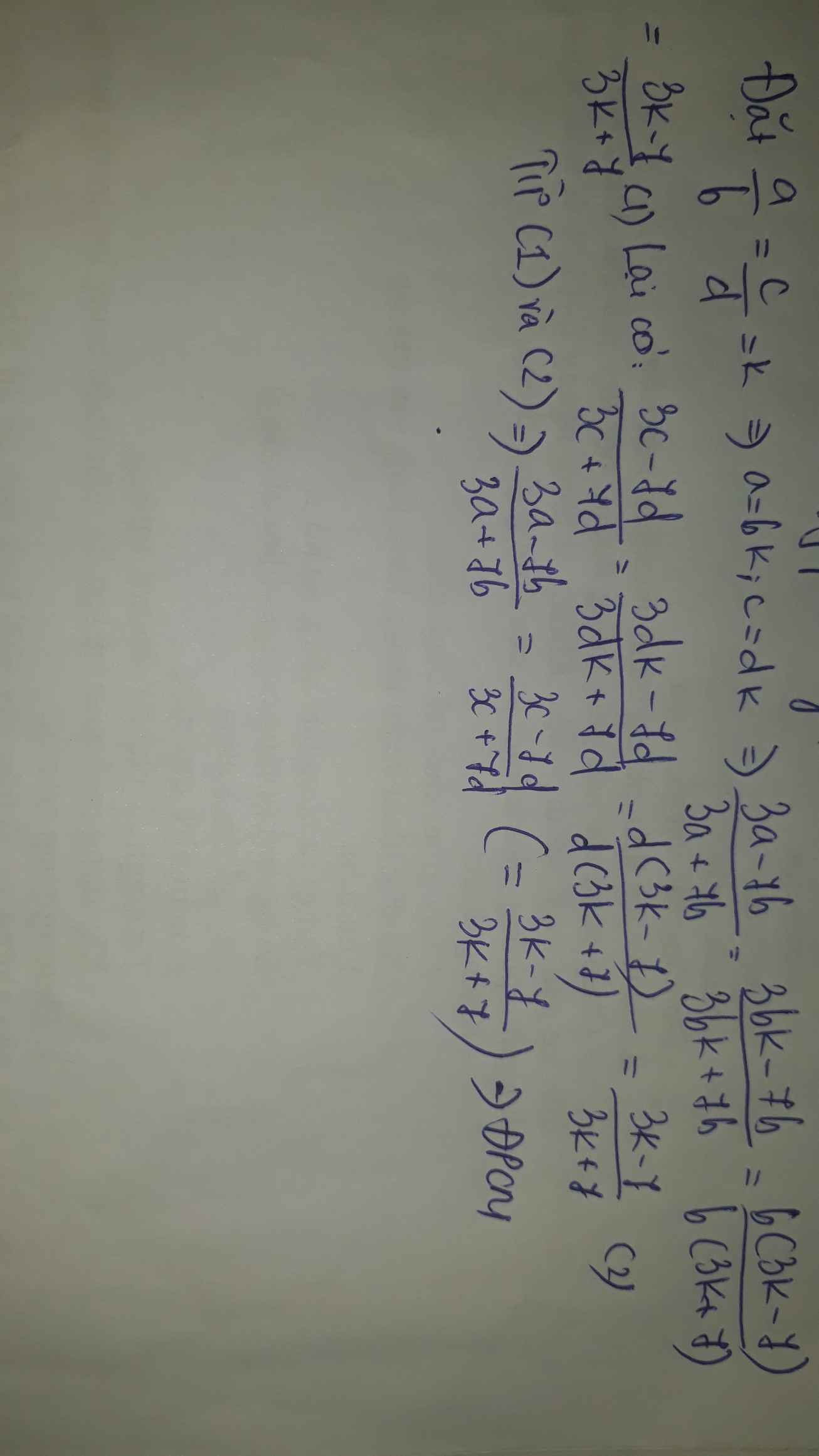cho a/b=c/d chưng tỏ:
3a+4b/3c+4d=6a+7b/6c+7d

Những câu hỏi liên quan
cho tỷ lệ thức a/b=c/d. chứng minh:
a, 2a+5b/3a-4b=2c+5d/3c-4d
b. 3a+7b/5a-7b=3c+7d/5c-7d
d. 4a+9b/4a-7b=4c+9d/4c-7d
giúp mình với ạ
Đặt \(\frac{a}{b}=\frac{c}{d}=k\)
=>a=bk; c=dk
a: \(\frac{2a+5b}{3a-4b}=\frac{2\cdot bk+5b}{3\cdot bk-4b}=\frac{b\left(2k+5\right)}{b\left(3k-4\right)}=\frac{2k+5}{3k-4}\)
\(\frac{2c+5d}{3c-4d}=\frac{2\cdot dk+5d}{3\cdot dk-4d}=\frac{d\left(2k+5\right)}{d\left(3k-4\right)}=\frac{2k+5}{3k-4}\)
Do đó: \(\frac{2a+5b}{3a-4b}=\frac{2c+5d}{3c-4d}\)
b: \(\frac{3a+7b}{5a-7b}=\frac{3\cdot bk+7b}{5\cdot bk-7b}=\frac{b\left(3k+7\right)}{b\left(5k-7\right)}=\frac{3k+7}{5k-7}\)
\(\frac{3c+7d}{5c-7d}=\frac{3\cdot dk+7d}{5\cdot dk-7d}=\frac{d\left(3k+7\right)}{d\left(5k-7\right)}=\frac{3k+7}{5k-7}\)
Do đó: \(\frac{3a+7b}{5a-7b}=\frac{3c+7d}{5c-7d}\)
d: \(\frac{4a+9b}{4a-7b}=\frac{4\cdot bk+9b}{4\cdot bk-7b}=\frac{b\left(4k+9\right)}{b\left(4k-7\right)}=\frac{4k+9}{4k-7}\)
\(\frac{4c+9d}{4c-7d}=\frac{4\cdot dk+9d}{4\cdot dk-7d}=\frac{d\left(4k+9\right)}{d\left(4k-7\right)}=\frac{4k+9}{4k-7}\)
Do đó: \(\frac{4a+9b}{4a-7b}=\frac{4c+9d}{4c-7d}\)
Đúng 0
Bình luận (0)
Cho: \(^{\dfrac{a}{b}=\dfrac{c}{d}\left(a,b,c,d\ne0\right)}\)
Chứng minh:
a) \(\dfrac{2a+7b}{3a-4b}=\dfrac{2c+7d}{3c-4d}\)
b) \(\dfrac{4a^2-5ab}{3a^2+7b^2}=\dfrac{4c^2-5cd}{3c^2+7d^2}\)
giúp mình gấp nha! Thanks
a/ Đặt :
\(\dfrac{a}{b}=\dfrac{c}{d}=k\) \(\Leftrightarrow\left\{{}\begin{matrix}a=bk\\c=dk\end{matrix}\right.\)
Ta có :
\(\dfrac{2a+7b}{3a-4b}=\dfrac{2bk+7b}{3bk-4b}=\dfrac{b\left(2k+7\right)}{b\left(3k-4\right)}=\dfrac{2k+7}{3k-4}\left(1\right)\)
\(\dfrac{2c+7d}{3c-4d}=\dfrac{2dk+7d}{3dk-4d}=\dfrac{d\left(2k+7\right)}{d\left(3k-4\right)}=\dfrac{2k+7}{3k-4}\)\(\left(2\right)\)
Từ \(\left(1\right)+\left(2\right)\Leftrightarrowđpcm\)
b/ tương tự
Đúng 0
Bình luận (0)
Cho tỉ lệ thức ab =cd . Chứng minh rằng ta cũng có các tỉ lệ thức sau:
\(\dfrac{5a-7b}{3a+4b}=\dfrac{5c-7d}{3c+4d}\)
1. Cho tỉ lệ thức: a/b = c/d chứng tỏ rằng:
2a + 5b/3a -4b = 2c + 5d/3c - 4d
Ta đặt:\(\frac{a}{b}=\frac{c}{d}=k\Rightarrow a=bk;c=dk\)
Khi đó: \(\frac{2a+5b}{3a-4b}=\frac{2bk+5b}{3bk-4b}=\frac{b\left(2k+5\right)}{b\left(3k-4\right)}=\frac{2k+5}{3k-4}\)
\(\frac{2c+5d}{3c-4d}=\frac{2dk+5d}{3dk-4d}=\frac{d\left(2k+5\right)}{d\left(3k-4\right)}=\frac{2k+5}{3k-4}\)
\(\Rightarrow\frac{2a+5b}{3a-4b}=\frac{2c+5d}{3c-4d}\left(=\frac{2k+5}{3k-4}\right)\)
Đúng 0
Bình luận (0)
Giải giúp mình với
Cho tỉ lệ thức \(\dfrac{a}{b}\)=\(\dfrac{c}{d}\)chứng minh các tỉ lệ thức\(\dfrac{3a-7b}{3a+7b}\)=\(\dfrac{3c-7d}{3c+7d}\)
Cho tỉ lệ thức \(\frac{a}{b}=\frac{c}{d}\). Chứng minh rằng ta cũng có các tỉ lệ thức sau:
a) \(\frac{5a-7b}{3a+4b}=\frac{5c-7d}{3c+4d}\)
b)\(\frac{\left(a+b\right)^2}{a^2+b^2}=\frac{\left(c+d\right)^2}{c^2+d^2}\)
giúp mình với, mai mình kiểm tra cuối kỉ rồi
Cho tỉ lệ thức \(\frac{3a+4b}{3a-4b}=\frac{3c+4d}{3c-4d}\). Chứng minh rằng \(\frac{a}{b}=\frac{c}{d}\).
Ta có: \(\frac{3a+4b}{3a-4b}=\frac{3c+4d}{3c-4d}\)
\(\Rightarrow\frac{3a+4b}{3a-4b}-1=\frac{3c+4d}{3c-4d}-1\)
\(\Leftrightarrow\frac{8b}{3a-4b}=\frac{8d}{3c-4d}\)
\(\Rightarrow b\left(3c-4d\right)=d\left(3a-4b\right)\)
\(\Leftrightarrow3bc=3ad\)
\(\Rightarrow\frac{a}{b}=\frac{c}{d}\left(đpcm\right)\)
cho tỉ lệ thức a/b. Chứng minh các tỉ lệ thức : 3a-7b/3a+7b=3c-7d/3c+7d
Cho \(\frac{a}{b}=\frac{c}{d}\)
CMR \(\frac{3a+7b}{3c+7d}=\frac{3a-7b}{3c-7d}\)
Ta có: \(\frac{a}{b}=\frac{c}{d}\)\(\Rightarrow a=bk,c=dk\)
\(\frac{3a+7b}{3c-7d}=\frac{3bk+7b}{3dk+7d}=\frac{b\left(3k+7\right)}{d\left(3k+7\right)}=\frac{b}{d}\)(1)
\(\frac{3a-7b}{3c-7d}=\frac{3bk-7b}{3dk-7d}=\frac{b\left(3k-7\right)}{d\left(3k-7\right)}=\frac{b}{d}\)(2)
Từ (1) và (2) \(\Rightarrow\frac{3a+7b}{3c+7d}=\frac{3a-7b}{3c-7d}\)
Đúng 0
Bình luận (0)